「あの治療を受けていたら、どうなっていたのだろう?」多くの人が一度は抱く疑問だろう。医学研究や社会科学において、特定の介入(治療、政策、プログラムなど)がもたらす効果を正確に知ることは非常に重要である。しかし、現実の世界では、誰がどの介入を受けるかは偶然ではなく、様々な要因に影響される。このような「選択バイアス」がある状況で、真の治療効果を推定するために強力なツールとなるのが「因果推論」の手法である。今回はその中でも、特に広く用いられている「逆確率重み付け(IPTW: Inverse Probability Treatment Weighting)」に焦点を当て、その基本的な考え方から具体的な計算方法までを解説する。
因果推論における治療効果推定
私たちが知りたいのは、「もし全員が治療を受けていたらどうなったか」と「もし全員が治療を受けなかったらどうなったか」という仮想的な状況間の比較である。これを「反事実(Counterfactual)」と呼ぶ。
具体的には、個々の対象者 $i$ について、治療を受けた場合の潜在的結果 $Y_i(1)$ と、治療を受けなかった場合の潜在的結果 $Y_i(0)$ の両方を考えることができる。しかし、現実には各対象者はどちらか一方の治療状態しか観察できない。例えば、治療を受けた人は $Y_i(1)$ は観測できるが $Y_i(0)$ は観測できない。この「観測できない反事実」が因果推論の最大の課題である。
治療効果の推定目標は、通常、以下のような**平均治療効果(ATE: Average Treatment Effect)**を推定することにある。
$$ATE = E[Y(1) – Y(0)]$$
あるいは、治療を受けた群における平均治療効果(ATT: Average Treatment Effect on the Treated)もよく用いられる。
$$ATT = E[Y(1) – Y(0) | T=1]$$
ここで $T$ は治療割り当てを示す変数($T=1$ が治療群、$T=0$ が対照群)である。
選択バイアスがある状況では、単純に治療群と対照群の平均アウトカムを比較しても、それは真の治療効果を反映しない。例えば、健康な人ほど治療を受ける傾向がある場合、治療群のアウトカムが高くても、それは治療の効果ではなく、元々の健康状態の違いによるものかもしれない。
因果推論では、このような選択バイアスを取り除くために様々な手法が開発されている。その一つがIPTWである。
IPTWによる治療効果推定概要
IPTWは、各対象者が実際に受けた治療(または受けなかった治療)を受ける確率の逆数で重み付けをすることで、選択バイアスを補正し、あたかもランダム化比較試験(RCT)のように治療群と対照群の背景因子が均等に分布するように調整する手法である。ただし、測定していない背景因子を潜在的均等にはできない点がRCTとは異なる。
基本的な考え方は以下の通りである。
- 傾向スコアの推定: まず、各対象者が治療を受ける確率(これを「傾向スコア」と呼ぶ)を推定する。傾向スコアは、共変量 $X$ が与えられた下での治療割り当ての条件付き確率 $e(X) = P(T=1 | X)$ として定義される。ロジスティック回帰モデルなどを用いて推定することが一般的である。
- 重みの計算: 推定された傾向スコアを用いて、各対象者に以下の重みを付与する。
- 治療群($T=1$)の場合: $w_i = \frac{1}{e(X_i)}$
- 対照群($T=0$)の場合: $w_i = \frac{1}{1 – e(X_i)}$
- 重み付けされた平均の計算: 各群の重み付けされた平均アウトカムを計算する。
- 治療群の重み付けされた平均: $E[Y(1)] \approx \frac{\sum_{i=1}^N Y_i \cdot T_i \cdot w_i}{\sum_{i=1}^N T_i \cdot w_i}$
- 対照群の重み付けされた平均: $E[Y(0)] \approx \frac{\sum_{i=1}^N Y_i \cdot (1-T_i) \cdot w_i}{\sum_{i=1}^N (1-T_i) \cdot w_i}$
- 治療効果の推定: 最後に、これらの重み付けされた平均アウトカムの差を計算することで、ATEを推定する。 $ATE_{IPTW} = \hat{E}[Y(1)] – \hat{E}[Y(0)]$
このIPTWの有効性は、「強く無視できる割り当て(Strongly Ignorable Treatment Assignment)」という仮定に基づいている。これは、「すべての関連する共変量 $X$ を条件付ければ、治療割り当てはアウトカムとは独立である」という仮定である。簡単に言えば、「観測された共変量 $X$ をすべて考慮すれば、治療を受けたか否かは完全にランダムである」と仮定できるということである。この仮定が満たされない場合(未測定の交絡因子が存在する場合など)、IPTWは真の因果効果を推定できない。つまり、未測定の交絡因子は必ず存在するため、IPTWがRCTに置き換わることはないことは留意したい。
具体例とR計算例
ここでは、架空のデータを用いてIPTWによる治療効果推定の具体例をRで示す。
シナリオ: ある薬(治療)が血圧(アウトカム)に与える影響を評価したい。しかし、この薬は、年齢や既存の健康状態が良い人に処方される傾向がある。
# データの生成 (例示用)
set.seed(123)
N <- 500 # サンプルサイズ
# 共変量: 年齢 (age) と既存の健康状態スコア (health_score)
age <- round(rnorm(N, 50, 10))
health_score <- round(rnorm(N, 70, 15))
# 治療割り当て (treatment): 年齢が若く、健康状態が良いほど治療を受ける確率が高い
# ロジスティック回帰の線形予測子
linear_predictor_t <- -2 + 0.05 * (80 - age) + 0.03 * health_score
prob_treatment <- 1 / (1 + exp(-linear_predictor_t))
treatment <- rbinom(N, 1, prob_treatment)
# アウトカム (blood_pressure): 治療が血圧を下げ、年齢が高いと血圧が高く、健康状態が良いと血圧が低い
# 真の治療効果は -5 とする
blood_pressure <- round(130 - 5 * treatment + 0.5 * age - 0.2 * health_score + rnorm(N, 0, 5))
# データフレームにまとめる
df <- data.frame(age, health_score, treatment, blood_pressure)
# 1. 傾向スコアの推定
# 共変量 (age, health_score) を用いて treatment を予測するロジスティック回帰モデル
propensity_model <- glm(treatment ~ age + health_score, data = df, family = binomial)
df$propensity_score <- predict(propensity_model, type = "response")
# 傾向スコアの範囲を確認 (0と1に近すぎる値がないか)
summary(df$propensity_score)
# 2. 重みの計算
df$weight <- ifelse(df$treatment == 1, 1 / df$propensity_score, 1 / (1 - df$propensity_score))
# 重みの分布を確認 (極端に大きな重みがないか)
summary(df$weight)
# 3. 重み付けされた平均の計算
# 治療群の重み付けされた平均アウトカム
weighted_mean_treated <- sum(df$blood_pressure[df$treatment == 1] * df$weight[df$treatment == 1]) / sum(df$weight[df$treatment == 1])
# 対照群の重み付けされた平均アウトカム
weighted_mean_control <- sum(df$blood_pressure[df$treatment == 0] * df$weight[df$treatment == 0]) / sum(df$weight[df$treatment == 0])
# 4. 治療効果の推定 (ATE)
ate_iptw <- weighted_mean_treated - weighted_mean_control
print(paste("IPTWによる平均治療効果 (ATE):", round(ate_iptw, 2)))
# 参考: 単純な平均比較 (バイアスあり)
naive_mean_treated <- mean(df$blood_pressure[df$treatment == 1])
naive_mean_control <- mean(df$blood_pressure[df$treatment == 0])
naive_diff <- naive_mean_treated - naive_mean_control
print(paste("単純な平均差:", round(naive_diff, 2)))
上記のRコードを実行すると、IPTWによる治療効果の推定値と、単純な平均比較による推定値が表示される。選択バイアスがある状況では、多くの場合、両者の値は異なる。
結果解釈例
実行結果:
> # 4. 治療効果の推定 (ATE)
> ate_iptw <- weighted_mean_treated - weighted_mean_control
> print(paste("IPTWによる平均治療効果 (ATE):", round(ate_iptw, 2)))
[1] "IPTWによる平均治療効果 (ATE): -4.04"
> # 参考: 単純な平均比較 (バイアスあり)
> naive_mean_treated <- mean(df$blood_pressure[df$treatment == 1])
> naive_mean_control <- mean(df$blood_pressure[df$treatment == 0])
> naive_diff <- naive_mean_treated - naive_mean_control
> print(paste("単純な平均差:", round(naive_diff, 2)))
[1] "単純な平均差: -6.59"この例では、単純な平均差が -6.59 となっているのに対し、IPTWによる推定値は -4.04 となった。これは、治療を受ける人が元々健康で血圧が低い傾向があったため、単純な比較では治療効果が過大評価されていた可能性を示唆している。IPTWによって、これらの選択バイアスが調整され、より真の治療効果に近い値(この例では真の値が-5)が推定されたと考えられる。
結果を解釈する際には、以下の点に留意する必要がある。
- 傾向スコアの妥当性: 傾向スコアのモデルが適切であったか(すべての重要な交絡因子を網羅していたか、モデルの適合度は高かったか)。
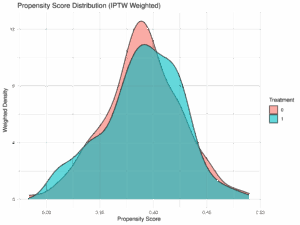
- 共通サポートの確認: 傾向スコアの分布において、治療群と対照群が重なる範囲(共通サポート)が十分にあるか。重ならない領域が多い場合、その領域のデータは実質的に比較できないため、IPTWの信頼性が低下する。
- 重みの安定性: 極端に大きな重みを持つデータ点がないか。これは傾向スコアが0や1に近い場合に発生しやすく、推定の不安定性につながる可能性がある。必要に応じて、重みのトリミング(上限を設定する)などの対処が検討されるが、これはバイアスとバリアンスのトレードオフとなる。
- 仮定の確認: 強く無視できる割り当ての仮定が満たされているか。これは観察データから直接確認することはできないが、未測定の交絡因子がないか、ドメイン知識(臨床専門分野における知識)に基づいて慎重に検討する必要がある。
まとめ
逆確率重み付け(IPTW)は、観測データから治療効果を推定するための強力な因果推論手法である。傾向スコアを用いて各対象者を重み付けすることで、選択バイアスを緩和し、あたかもランダム化されたかのような状況を作り出すことができる。
しかし、その適用には、傾向スコアの適切なモデリング、共通サポートの確認、そして何よりも「強く無視できる割り当て」の仮定への理解と検討が不可欠である。これらの点を踏まえ、慎重に適用することで、IPTWは現実世界の複雑なデータから、より信頼性の高い因果的知見を引き出すための強力な武器となるだろう。因果推論の世界は奥深く、IPTWはその入り口の一つに過ぎない。さらに学びを深め、データから真の洞察を得るための旅を続けていこう。





コメント