データ分析において、複数のグループ間での関係性の違いを比較することは非常に重要だ。特に、ある従属変数と独立変数の関係が、別の要因(グループ)によってどのように異なるかを明らかにしたい場合、回帰直線の差の検定は強力なツールとなる。しかし、ここで見落としてはいけないのが「交絡因子」の存在だ。交絡因子を考慮せずに解析を進めると、誤った結論を導き出す可能性がある。
この記事では、交絡因子を考慮した回帰直線の差の検定について、具体的な例とRでの計算例、そして結果の可視化を交えて解説する。
回帰直線の差の検定とは何か?
回帰直線の差の検定とは、2つ以上のグループ間で、ある独立変数と従属変数の間の線形関係(回帰直線)に統計的に有意な差があるかどうかを評価する手法だ。具体的には、切片と傾きの両方、またはそのいずれかに差があるかを検定する。
交絡因子とは何か?なぜ重要なのか?
交絡因子(Confounding Factor)とは、独立変数と従属変数の両方に影響を与え、その結果、両者の間に見かけ上の関連性を作り出したり、真の関連性を隠蔽したりする第三の変数のことだ。
例えば、「コーヒーの摂取量」と「心臓病のリスク」の関係を調べたいとする。ここで「喫煙習慣」という交絡因子が存在するかもしれない。喫煙者はコーヒーを飲む量が多い傾向があり、かつ喫煙自体が心臓病のリスクを高める。この場合、コーヒーと心臓病の間に見られる関連性が、実は喫煙習慣によって引き起こされている可能性があり、コーヒー自体が心臓病の原因ではないかもしれない。
回帰直線の差の検定を行う際にも、交絡因子を無視すると、グループ間の真の関係性の違いを見誤る可能性があるのだ。
具体例で考えてみよう:新薬の有効性
ある疾患に対する新薬Aと既存薬Bの効果を比較したいとする。効果の指標として「症状改善度(スコア:0-100)」、影響を与える要因として「投薬期間(週)」を考える。しかし、患者の「年齢」が、投薬期間と症状改善度の両方に影響を与える可能性があり、これが交絡因子となり得る。
- 独立変数: 投薬期間
- 従属変数: 症状改善度
- グループ変数: 薬剤(A vs B)
- 交絡因子: 年齢
私たちは、「新薬Aと既存薬Bで、投薬期間が症状改善度に与える影響(回帰直線)に差があるか、ただし年齢の影響を調整した上で」を知りたいわけだ。
Rでの計算例と可視化
それでは、Rを使って上記の例をシミュレーションし、解析してみよう。
まず、必要なパッケージを読み込み、ダミーデータを作成する。
Rスクリプト例:
# 必要なパッケージをインストール&読み込み(まだインストールしていない場合)
# install.packages("ggplot2")
# install.packages("dplyr")
library(ggplot2)
library(dplyr)
# ダミーデータの作成
set.seed(123) # 再現性のためのシード設定
# 薬剤Aのデータ
data_A <- data.frame(
薬剤 = "A",
投薬期間 = round(runif(100, 1, 10)), # 1週間から10週間
年齢 = sample(30:70, 100, replace = TRUE) # 30歳から70歳
)
data_A$症状改善度 <- round(30 + 5 * data_A$投薬期間 - 0.5 * data_A$年齢 + rnorm(100, 0, 5))
# 薬剤Bのデータ
data_B <- data.frame(
薬剤 = "B",
投薬期間 = round(runif(100, 1, 10)),
年齢 = sample(30:70, 100, replace = TRUE)
)
data_B$症状改善度 <- round(20 + 6 * data_B$投薬期間 - 0.4 * data_B$年齢 + rnorm(100, 0, 5))
# データを結合
data_all <- rbind(data_A, data_B)
# 薬剤を因子型に変換
data_all$薬剤 <- as.factor(data_all$薬剤)
# データの一部を表示
head(data_all)
回帰直線の可視化
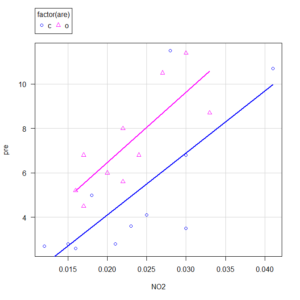
まず、回帰直線を可視化して、視覚的に違いを把握しよう。交絡因子を調整したモデルの可視化は少し複雑になるが、ここでは単純に各グループの回帰直線をプロットする。ただし、交絡因子の影響を可視化する際には、例えば年齢を特定の値に固定してプロットするといった工夫が必要になる。ここでは簡略化のため、年齢の影響は直接的には可視化せず、各薬剤グループの散布図と回帰直線を表示する。
# 可視化
ggplot(data_all, aes(x = 投薬期間, y = 症状改善度, color = 薬剤)) +
geom_point(alpha = 0.6) + # 散布図
geom_smooth(method = "lm", se = FALSE) + # 各グループの回帰直線
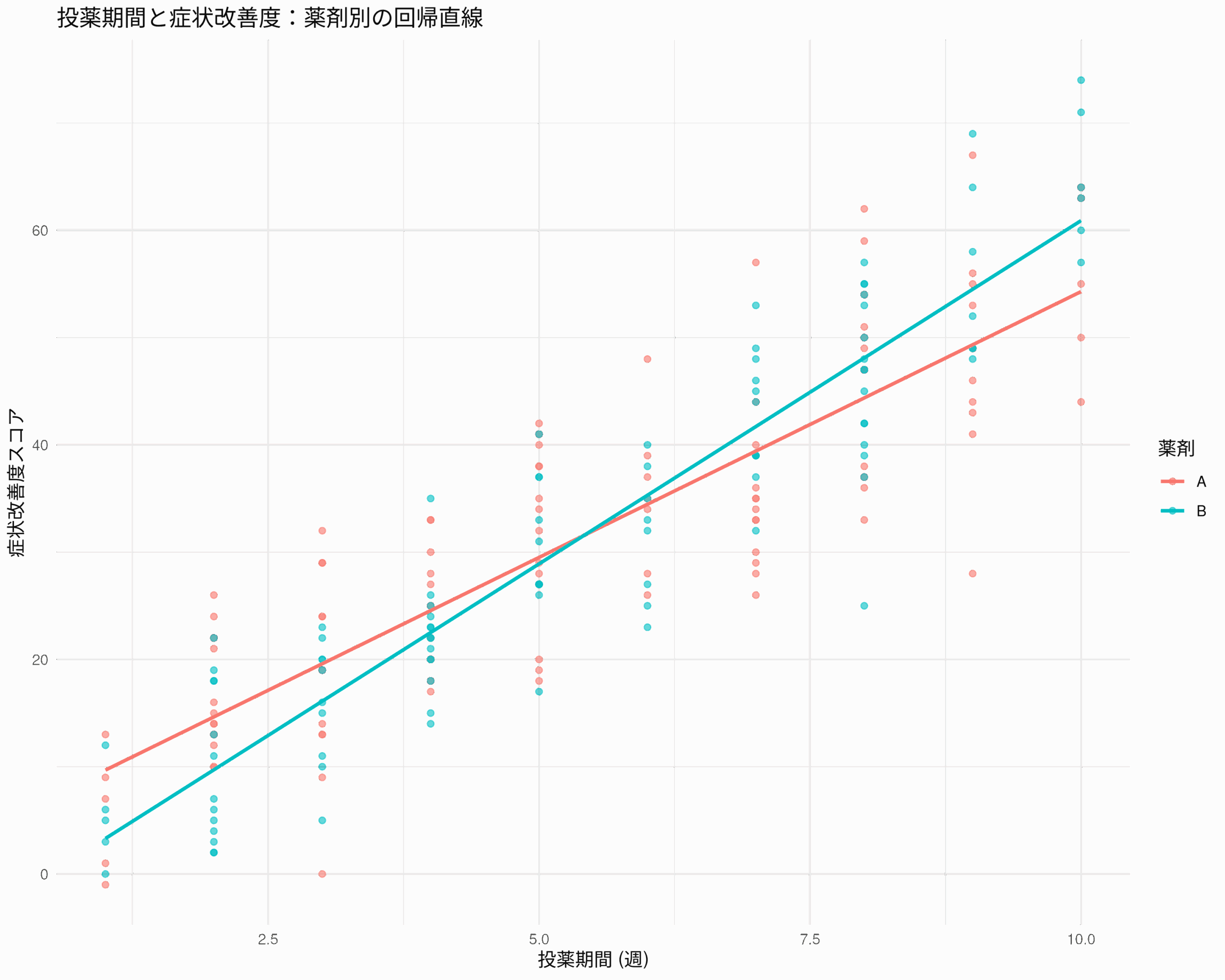
labs(title = "投薬期間と症状改善度:薬剤別の回帰直線",
x = "投薬期間 (週)",
y = "症状改善度スコア") +
theme_minimal()
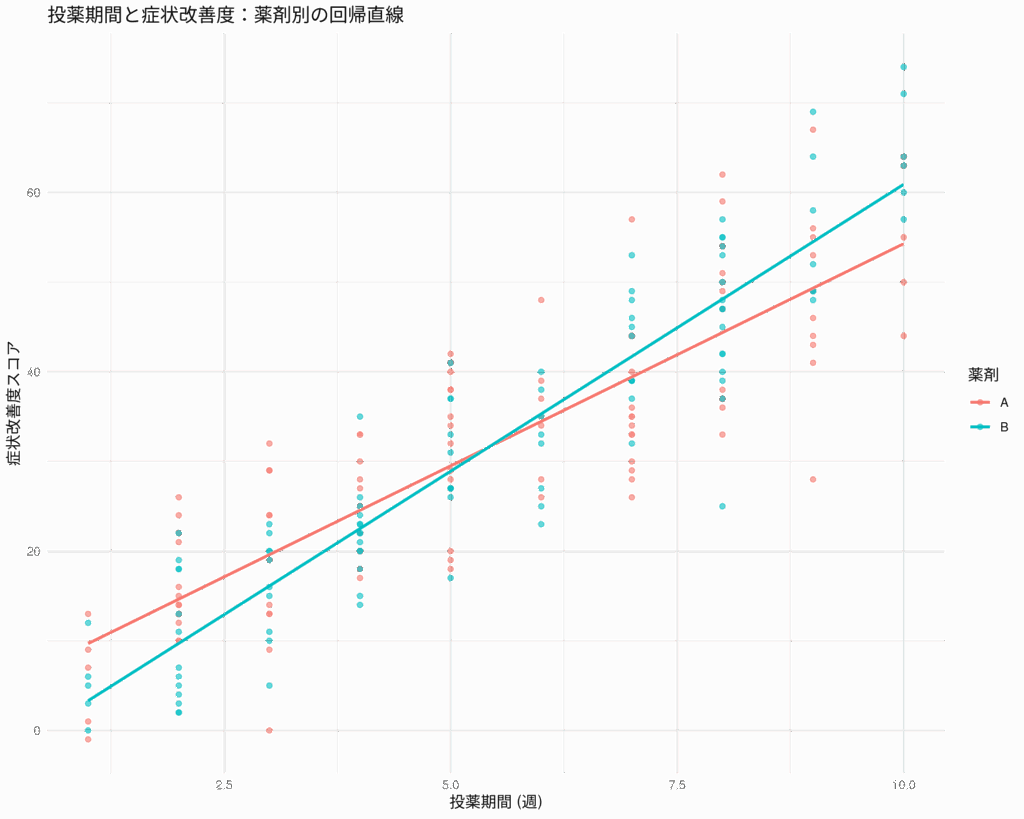
このグラフでは、2つの回帰直線が描かれ、その傾きや位置の違いを視覚的に確認できる。ただし、これは年齢の調整がなされていない単純なプロットであることに注意してほしい。より厳密な可視化には、予測値を使ったプロットなどが必要になる。
交絡因子を考慮しない場合
まずは、年齢を考慮せずに単純に薬剤グループごとの回帰直線の差を検定してみよう。これは、薬剤と投薬期間の交互作用項を用いることで検定できる。
# 交絡因子を考慮しないモデル
model_simple <- lm(症状改善度 ~ 投薬期間 * 薬剤, data = data_all)
summary(model_simple)
実行結果:
> # 交絡因子を考慮しないモデル
> model_simple <- lm(症状改善度 ~ 投薬期間 * 薬剤, data = data_all)
> summary(model_simple)
Call:
lm(formula = 症状改善度 ~ 投薬期間 * 薬剤, data = data_all)
Residuals:
Min 1Q Median 3Q Max
-23.1056 -5.4419 -0.4874 5.0322 17.6681
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.7327 1.7365 2.725 0.00700 **
投薬期間 4.9555 0.2876 17.229 < 2e-16 ***
薬剤B -7.8197 2.4408 -3.204 0.00158 **
投薬期間:薬剤B 1.4436 0.4044 3.569 0.00045 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.471 on 196 degrees of freedom
Multiple R-squared: 0.8039, Adjusted R-squared: 0.8009
F-statistic: 267.8 on 3 and 196 DF, p-value: < 2.2e-16
summary(model_simple) の出力を見ると、投薬期間:薬剤B の交互作用項のp値を確認する。このp値が統計的に有意であれば、薬剤Aと薬剤Bで投薬期間の傾きに差があると解釈できる。また、薬剤B の項は切片の差を示す。
交絡因子を考慮する場合
次に、交絡因子である「年齢」をモデルに投入して、回帰直線の差を検定する。
# 交絡因子を考慮したモデル
model_confounder <- lm(症状改善度 ~ 投薬期間 * 薬剤 + 年齢, data = data_all)
summary(model_confounder)
実行結果:
> # 交絡因子を考慮したモデル
> model_confounder <- lm(症状改善度 ~ 投薬期間 * 薬剤 + 年齢, data = data_all)
> summary(model_confounder)
Call:
lm(formula = 症状改善度 ~ 投薬期間 * 薬剤 + 年齢,
data = data_all)
Residuals:
Min 1Q Median 3Q Max
-14.4094 -3.7725 0.1532 3.5748 13.2856
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 26.39517 2.00814 13.144 < 2e-16 ***
投薬期間 5.21210 0.20650 25.240 < 2e-16 ***
薬剤B -5.11506 1.75625 -2.912 0.004004 **
年齢 -0.45557 0.03319 -13.725 < 2e-16 ***
投薬期間:薬剤B 0.98338 0.29111 3.378 0.000882 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.342 on 195 degrees of freedom
Multiple R-squared: 0.9002, Adjusted R-squared: 0.8982
F-statistic: 439.9 on 4 and 195 DF, p-value: < 2.2e-16
summary(model_confounder) の出力を見る。ここでも 投薬期間:薬剤B の交互作用項のp値が重要だ。このp値が統計的に有意であれば、「年齢の影響を調整した上で」、薬剤Aと薬剤Bで投薬期間の傾きに差があると言える。また、薬剤B の項は調整後の切片の差を示す。
年齢の係数も確認し、年齢が症状改善度に影響を与えているかどうかも確認できるだろう。年齢の Estimate がマイナスなので、加齢とともに症状改善度が下がると理解できる。
補足:交絡因子投入で交互作用が有意でなくなった場合
もし交絡因子をモデルに投入した結果、それまで統計的に有意だった交互作用項(回帰直線の傾きの差)が有意でなくなった場合、それは非常に重要なサインだ。
この場合、「当初見られたグループ間の回帰直線の傾きの違いは、実際にはその交絡因子によって引き起こされていた、あるいは強く影響を受けていた」と解釈できる。つまり、見かけ上の差が、実は交絡因子の影響であった可能性が高いのだ。
簡単な言葉で言うと、交絡因子が「真犯人」で、私たちが当初見ていたグループ間の違いは、その「真犯人」が引き起こした影のようなものだった、と理解できる。この結果は、私たちが本当に知りたい独立変数と従属変数の関係について、より正確な理解を与えてくれるものとなる。
まとめ
交絡因子を考慮した回帰直線の差の検定は、単にグループ間の関係性の違いを見るだけでなく、その違いが本当に知りたい変数によって引き起こされているのか、それとも他の隠れた要因によって見せかけられたものなのかを判断するために不可欠だ。
今回のRの例では、交絡因子である「年齢」をモデルに含めることで、結果は大きく異なることはなかったが、より正確な回帰直線の差の検定を行うことができた。データ分析を行う際には、常に潜在的な交絡因子の存在を意識し、適切にモデルに組み込むことで、よりロバストで信頼性の高い結論を導き出すように心がけよう。





コメント