R で重回帰分析の変数選択に参考となる計算上ベストな変数セットを提案してくれる方法

R で重回帰分析を行った際の変数選択の方法の解説。

bestglmの準備とサンプルデータ

R の bestglm() 関数は、AIC, BIC(デフォルト), BICqなどの Information Criterion 情報規準を使って ベストの変数の組み合わせを見つけてくれる。

bestglmパッケージのznuclearデータで試してみる。

事前にインストールしておいたあと bestglmを呼び出す。

install.packages("bestglm")

library(bestglm)

znuclearデータフレームは、原発のデータ。

Data on 32 nuclear power plants. The response variable is cost and there are ten covariates.

bestglmの場合、data.frame内で、 カラムの順番に決まりがある。

まず独立変数を並べて、 一番最後のカラムに従属変数を置く。  

このdata.frameではcostが従属変数だ。

以下のような順番に並んでいる必要がある。

右端がcost。

> round(znuclear, 2)
    date    T1    T2 capacity PR NE CT BW     N PT  cost
1  68.58  0.19 -1.72    -0.62  0  1  0  0  0.89  0  0.17
2  67.33 -1.17  1.01     1.14  0  0  1  0 -1.80  0  0.13
3  67.33 -1.17  1.91     1.14  1  0  1  0 -1.80  0  0.07
4  68.00 -0.79  0.50     1.14  0  1  1  0  0.73  0  1.09
5  68.00 -0.79  1.40     1.14  1  1  1  0  0.73  0  1.05
6  67.92 -0.11 -1.11    -1.79  0  1  1  0 -0.68  0 -0.59
7  68.17 -0.43 -1.23     0.10  0  0  0  0 -0.16  0 -1.22
8  68.42  0.19 -0.25    -2.26  0  0  0  0 -1.80  0 -0.81
9  68.42  0.47 -0.66     0.10  1  0  0  0 -0.16  0  0.15
10 68.33 -0.43  0.85    -0.05  0  1  1  1 -1.09  0  1.24
11 68.58 -0.43  0.23    -1.45  0  0  0  0 -0.68  0 -0.55
12 68.75 -0.11 -1.59    -0.06  0  1  0  0  0.02  0 -0.18
13 68.42  0.47  0.05    -1.67  0  0  1  0 -1.09  0 -0.12
14 68.92  0.98 -1.00     1.08  0  0  0  0  0.18  0  0.37
15 68.92 -0.11  0.32     0.23  0  0  0  1  1.02  0 -0.24
16 68.42 -0.79  0.50    -0.12  0  0  0  0 -0.68  0 -0.05
17 69.50  1.21 -0.15     0.21  0  1  0  0  1.08  0  1.33
18 68.42  0.47  1.25    -1.67  1  0  1  0 -1.09  0 -1.05
19 69.17  0.47  0.50     1.23  0  0  0  0 -1.80  0  1.89
20 68.92  0.73 -0.25     1.08  1  0  0  0  0.32  0  0.34
21 68.75 -0.79  0.76     0.52  0  0  1  1  0.96  0  0.73
22 70.92  2.02 -0.45     0.13  1  1  0  0  1.25  0  1.15
23 69.67  0.73 -0.25    -0.08  0  0  1  0  1.14  0  0.97
24 70.08  1.43 -0.35     0.09  1  0  0  0 -0.68  0  0.91
25 70.42  1.43 -1.98    -1.61  0  0  1  0  1.20  0  0.25
26 71.08  1.64 -0.45     1.38  0  0  1  0  1.30  0  1.27
27 67.25 -0.11  0.14    -0.30  0  0  0  0  0.32  1 -1.94
28 67.17 -1.60 -1.47     0.09  0  0  1  0  0.18  1 -1.07
29 67.83 -0.43  0.14     0.40  0  0  0  1  0.64  1 -1.10
30 67.83 -0.43  0.85     0.40  1  0  0  1  0.64  1 -1.14
31 67.25 -0.11  0.93    -0.30  1  0  0  0  0.32  1 -1.81
32 67.83 -2.62  1.55     0.40  1  0  0  1  0.64  1 -1.23

bestglmの実行と結果

bestglm()の結果を見てみる。

BICで検討したBest Modelが表示される。

> out <- bestglm(znuclear)
> out
BIC
BICq equivalent for q in (0.349204366418933, 0.716418902103362)
Best Model:
               Estimate Std. Error   t value     Pr(>|t|)
(Intercept) -38.7480703 7.91826983 -4.893502 4.910313e-05
date          0.5620284 0.11445901  4.910303 4.701224e-05
capacity      0.4759804 0.07818015  6.088252 2.310934e-06
NE            0.6588957 0.19616044  3.358963 2.510375e-03
CT            0.3714664 0.15987847  2.323430 2.858187e-02
N            -0.2277672 0.10786682 -2.111560 4.489115e-02
PT           -0.5982476 0.30044058 -1.991235 5.748951e-02

summary()でBest modelのモデルの有意性が確認できる。

> summary(out)
Fitting algorithm:  BIC-leaps
Best Model:
df  deviance
Null Model 25  4.436699
Full Model 31 31.000000
likelihood-ratio test - GLM
data:  H0: Null Model vs. H1: Best Fit BIC-leaps
X = 26.563, df = 6, p-value = 0.0001748

out$Subsetsで、検討したモデル一覧が表示される。

＊がBest model。

> out$Subsets
    (Intercept)  date    T1    T2 capacity    PR    NE    CT    BW     N    PT logLikelihood        BIC
0          TRUE FALSE FALSE FALSE    FALSE FALSE FALSE FALSE FALSE FALSE FALSE     0.5079792  -1.015958
1          TRUE FALSE FALSE FALSE    FALSE FALSE FALSE FALSE FALSE FALSE  TRUE    10.2059259 -16.946116
2          TRUE FALSE FALSE FALSE     TRUE FALSE FALSE FALSE FALSE FALSE  TRUE    17.8241085 -28.716745
3          TRUE  TRUE FALSE FALSE     TRUE FALSE FALSE FALSE FALSE FALSE  TRUE    23.3113617 -36.225516
4          TRUE  TRUE FALSE FALSE     TRUE FALSE  TRUE FALSE FALSE FALSE  TRUE    26.6826218 -39.502300
5          TRUE  TRUE FALSE FALSE     TRUE FALSE  TRUE  TRUE FALSE  TRUE FALSE    29.2577991 -41.186919
6*         TRUE  TRUE FALSE FALSE     TRUE FALSE  TRUE  TRUE FALSE  TRUE  TRUE    31.6132054 -42.431995
7          TRUE  TRUE FALSE FALSE     TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE    32.1063164 -39.952482
8          TRUE  TRUE FALSE  TRUE     TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE    33.2254075 -38.724928
9          TRUE  TRUE  TRUE  TRUE     TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE    33.2836564 -35.375690
10         TRUE  TRUE  TRUE  TRUE     TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE    33.3647536 -32.072148

  out$BestModelsで、Bestから5番目までが表示される。

> out$BestModels
  date    T1    T2 capacity    PR   NE   CT    BW     N    PT Criterion
1 TRUE FALSE FALSE     TRUE FALSE TRUE TRUE FALSE  TRUE  TRUE -42.43200
2 TRUE FALSE FALSE     TRUE FALSE TRUE TRUE FALSE  TRUE FALSE -41.18692
3 TRUE FALSE FALSE     TRUE FALSE TRUE TRUE FALSE FALSE  TRUE -40.64612
4 TRUE FALSE FALSE     TRUE FALSE TRUE TRUE  TRUE  TRUE  TRUE -39.95248
5 TRUE FALSE FALSE     TRUE  TRUE TRUE TRUE FALSE  TRUE  TRUE -39.84694

  out$BestModelで、Best modelのcoefficientsだけが表示される。

> out$BestModel
Call:
lm(formula = y ~ ., data = data.frame(Xy[, c(bestset[-1], FALSE),
drop = FALSE], y = y))
Coefficients:
(Intercept)         date     capacity           NE           CT            N           PT
-38.7481       0.5620       0.4760       0.6589       0.3715      -0.2278      -0.5982

Best modelのresidualを用いてQQ plotを描くことができる。

qqnorm(resid(out$BestModel), ylab="residuals, best model")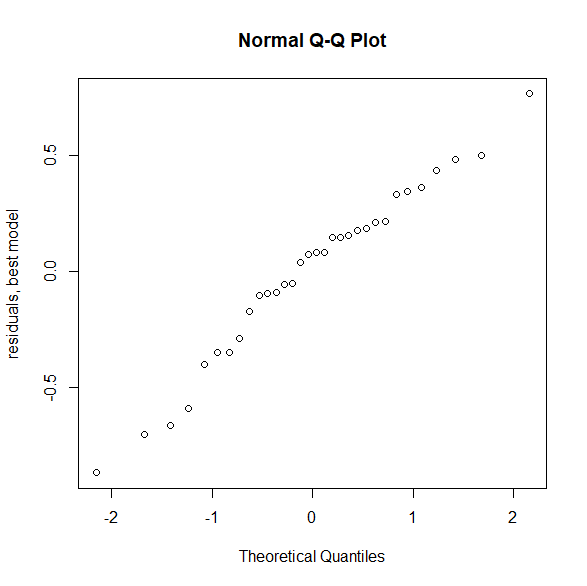

まとめ

重回帰分析において情報規準によってベストの変数選択を教えてくれる bestglm() の使い方を解説した。

もちろん計算上もっとも当てはまりのよいモデルを教えてくれているだけで、 変数の選択には変数の意味合いは全く加味されていない。

研究者はこの結果を参考に、 先行研究の結果及び理屈の上での関連性を総合して、自分で最終解析変数セットを決めなければならない。