重回帰分析は、複数の説明変数を用いて目的変数を予測する強力な統計手法である。しかし、OLS(Ordinary Least Squares:通常の最小二乗法)を適用する際に、ある重要な仮定が満たされない場合、そのモデルの信頼性が損なわれることがある。それが「等分散性」の仮定である。
本記事では、この等分散性の仮定が満たされない場合に有効な「重み付き最小二乗法(Weighted Least Squares: WLS)」について、その概要、意義、具体的な適用例、そして統計ソフトウェアRを用いた計算例と結果の解釈までを詳しく解説する。
重み付き最小二乗法(WLS)とは?
概要
重み付き最小二乗法は、OLSの拡張であり、各観測値に異なる「重み」を割り当てることで、異なった分散を持つデータ(不均一分散:Heteroscedasticity)に対処する回帰分析手法である。OLSでは、すべての観測値が等しい分散を持つと仮定するが、WLSではこの仮定を緩和し、分散の小さい観測値には大きな重みを、分散の大きい観測値には小さな重みを割り当てる。これにより、よりばらつきの少ない、信頼性の高い観測値がモデル推定により大きく貢献するようになる。
意義
WLSを用いる意義は以下の点にある。
- 効率的な推定量の獲得: 不均一分散が存在するOLSでは、推定量の分散が最小ではなくなり、効率的な推定が行えない。WLSを用いることで、最小分散不偏推定量(BLUE: Best Linear Unbiased Estimator)に近い、より効率的な推定量を獲得することができる。
- 信頼性の高い推論: 正しい標準誤差を推定できるため、係数の有意性検定や信頼区間の推定がより正確になる。これにより、モデルの解釈や予測の信頼性が向上する。
- モデルの適合性向上: 不均一分散を考慮することで、データ構造により適合したモデルを構築できる。
具体例:所得と教育年数と貯蓄額
ある地域の住民の所得、教育年数、貯蓄額に関するデータを収集したと仮定する。所得と教育年数を説明変数、貯蓄額を目的変数として重回帰分析を行うことを考える。
このデータでは、所得が高い人ほど貯蓄額のばらつきが大きい(つまり、高所得者の中には貯蓄をたくさんする人もいれば、あまりしない人もいる)という傾向が見られるかもしれない。これは不均一分散の一例である。このような場合、所得が低い人々の貯蓄額の予測は比較的正確である一方、所得が高い人々の貯蓄額の予測はばらつきが大きくなるため、OLSでは高所得者のデータがモデル推定に過度に影響を与えてしまう可能性がある。
そこで、WLSを適用し、貯蓄額のばらつきが小さい(分散が小さい)観測値(例えば所得の低い人々のデータ)には大きな重みを、貯蓄額のばらつきが大きい(分散が大きい)観測値(所得の高い人々のデータ)には小さな重みを割り当てることで、より適切な回帰モデルを構築することができる。
Rでの計算例と結果解釈
ここでは、Rを用いてWLSの計算例を示す。架空のデータを作成して説明する。
# 必要なライブラリをロード
library(lmtest) # 共分散行列を推定するために必要
# 架空のデータを生成
set.seed(123)
n <- 100
income <- round(runif(n, 300, 1000)) # 所得 (単位: 万円)
education <- round(sample(8:18, n, replace = TRUE)) # 教育年数
# 貯蓄額に不均一分散を導入
saving <- round(50 + 0.1 * income + 5 * education + rnorm(n, 0, income * 0.05))
# データフレームを作成
data <- data.frame(income, education, saving)
# 不均一分散の確認 (残差プロット)
# まずは通常のOLSを実行
ols_model <- lm(saving ~ income + education, data = data)
par(mfrow = c(2, 1), mar = c(4, 5, 2, 2), oma = c(0, 0, 2, 0), cex.main = 1.5, cex.lab = 1.5, cex.axis = 1.5)
plot(ols_model$fitted.values, ols_model$residuals,
xlab = "予測値", ylab = "残差",
main = "OLS回帰の残差プロット")
abline(h = 0, col = "red", lty = 2)
# 残差が予測値の増加とともに広がる傾向が見られる場合、不均一分散が疑われる
# 重みを決定(分散の逆数を重みとする)
# ここでは簡略化のため、incomeが大きいほど分散が大きいと仮定し、incomeの逆数を重みとする
# より厳密には、分散関数をモデル化して重みを決定するが、ここでは簡略化
weights <- 1 / income
# 重み付き最小二乗法 (WLS) を実行
wls_model <- lm(saving ~ income + education, data = data, weights = weights)
# 結果のサマリー
summary(ols_model)
summary(wls_model)
# 結果の比較 (係数と標準誤差)
# OLSの係数と標準誤差
ols_coef <- coef(summary(ols_model))
ols_coef_df <- as.data.frame(ols_coef)
colnames(ols_coef_df) <- c("OLS Estimate", "OLS Std. Error", "OLS t value", "OLS Pr(>|t|)")
# WLSの係数と標準誤差
wls_coef <- coef(summary(wls_model))
wls_coef_df <- as.data.frame(wls_coef)
colnames(wls_coef_df) <- c("WLS Estimate", "WLS Std. Error", "WLS t value", "WLS Pr(>|t|)")
# 比較のためにデータフレームを結合
results_comparison <- merge(ols_coef_df, wls_coef_df, by = 0)
rownames(results_comparison) <- results_comparison$Row.names
results_comparison <- results_comparison[, -1]
print(results_comparison)
実行結果:
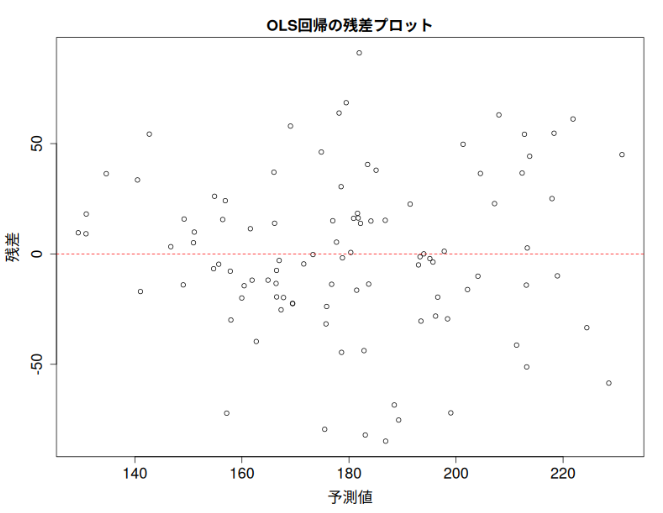
不均一分散の確認 (残差プロット)で、残差が予測値の増加とともに広がる傾向が見られる場合、不均一分散が疑われる(今回の場合はそれほどでもないが、不均一分散が疑われたことと仮定して進める)
> # 結果のサマリー
> summary(ols_model)
Call:
lm(formula = saving ~ income + education, data = data)
Residuals:
Min 1Q Median 3Q Max
-84.853 -19.630 -1.528 22.628 91.078
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 44.31370 21.86490 2.027 0.0454 *
income 0.08845 0.01837 4.815 5.42e-06 ***
education 5.80067 1.28243 4.523 1.73e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 36.41 on 97 degrees of freedom
Multiple R-squared: 0.298, Adjusted R-squared: 0.2835
F-statistic: 20.59 on 2 and 97 DF, p-value: 3.533e-08
> summary(wls_model)
Call:
lm(formula = saving ~ income + education, data = data, weights = weights)
Weighted Residuals:
Min 1Q Median 3Q Max
-3.06394 -0.87100 -0.03169 0.84237 3.00088
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 60.74260 19.67855 3.087 0.00264 **
income 0.08086 0.01700 4.757 6.85e-06 ***
education 4.94611 1.15245 4.292 4.20e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.366 on 97 degrees of freedom
Multiple R-squared: 0.2765, Adjusted R-squared: 0.2615
F-statistic: 18.53 on 2 and 97 DF, p-value: 1.528e-07
>
> print(results_comparison)
OLS Estimate OLS Std. Error OLS t value OLS Pr(>|t|) WLS Estimate
(Intercept) 44.31369826 21.86489811 2.026705 4.543732e-02 60.74260273
education 5.80067082 1.28242638 4.523200 1.725943e-05 4.94611068
income 0.08844673 0.01837012 4.814707 5.424308e-06 0.08085543
WLS Std. Error WLS t value WLS Pr(>|t|)
(Intercept) 19.67854732 3.086742 2.638157e-03
education 1.15245335 4.291810 4.198862e-05
income 0.01699848 4.756626 6.853118e-06
> 結果の解釈
上記のRコードを実行すると、OLSとWLSそれぞれの回帰結果のサマリーが表示され、さらに両者の係数と標準誤差が比較して見られるような一覧が出力される。
- 残差プロット: OLSモデルの残差プロットを見ると、不均一文さが存在する場合、予測値の増加とともに残差のばらつきが大きくなっていることが視覚的に確認できる。
- 係数の比較: OLSとWLSで推定される係数の値は、必ずしも大きく変わらないかもしれないが、重要なのは標準誤差である。
- 標準誤差の比較: WLSモデルでは、OLSモデルと比較して、各係数の標準誤差が小さくなっていることが期待される。特に、不均一分散の影響を強く受ける変数(上記の例では所得)の係数において、その効果が顕著に現れることになる。標準誤差が小さいということは、推定された係数の信頼性が高いことを意味する(今回の例ではそれほど大きな変化はなかったが、0.0184 から0.0170 と若干小さくなった)
- t値とp値: 標準誤差が小さくなることで、t値が大きくなり、p値が小さくなる傾向が見られる(上記の例は当てはまらないが)。これにより、OLSでは統計的に有意でなかった係数が、WLSでは有意になる可能性がある。これは、WLSがより効率的な推定を可能にし、より正確な統計的推論を導くことを示している。
まとめ
重み付き最小二乗法は、データに不均一分散が存在する場合に、通常の最小二乗法よりも信頼性の高い回帰モデルを構築するための強力なツールである。各観測値のばらつきの大きさに応じて適切な重みを割り当てることで、より効率的な係数推定と、より正確な統計的推論を可能にする。
WLSを適用する際には、適切な重みの選択が重要となる。重みは、分散の逆数として定義されることが多いが、その分散関数をどのように推定するかは、データの特性や分析の目的に応じて慎重に検討する必要がある。本記事が、重回帰分析におけるWLSの理解を深める一助となれば幸いである。





コメント