連続データの代表的な要約値、平均値と標準偏差を統合するにはどうやったらよいか?
連続データを層別で要約値を求めた後に統合する方法。
連続データの層別解析の統合とは?
目的変数としての連続データに対して、交絡を調整しながら分析するには、共分散分析と呼ばれる線形回帰モデルを用いればよいが、何かの都合で、層別に連続データを集計しそれを統合する必要がある場合、どうやったらよいか?
代表的な要約統計量、平均値と標準偏差の統合を紹介したい。
ちなみに、メタアナリシスとして2群の平均値の差の統合を行うには、以下の記事を参照。
連続データの層別解析の統合はどのような計算をするのか?
平均の統合(重み付け平均)
平均値の統合は以下の式のように、各群のサンプルサイズを重みとした、重み付け平均 $ \bar{X_t} $ を計算する。
$$ \bar{X_t} = \frac{\sum{n \bar{X}}}{n_t} $$
ここで、n は各群のサンプルサイズ、$ \bar{X} $ は各群の平均値、$ n_t $ は全群のサンプルサイズの合計である。
標準偏差の統合
標準偏差は以下のように計算する。
U は各群の標準偏差を2乗して計算した不偏分散である。
$$ \sqrt{\frac{\sum{(n – 1) U} + \sum{n(\bar{X} – \bar{X_t})^2}}{n_t – 1}} $$
連続データの層別解析の統合を実際にやってみる
こちらのリンク先にある例題を使って実際にやってみる。
群ごとの平均値・不偏分散を統合する方法とは何? わかりやすく解説 Weblio辞書
| 群 | 都道府県数 | 平均値 | 標準偏差 |
|---|---|---|---|
| 第1群 | 8 | 135.83 | 19.59 |
| 第2群 | 11 | 160.49 | 12.28 |
| 第3群 | 22 | 178.35 | 15.01 |
| 第4群 | 6 | 188.06 | 9.81 |
R でやってみる
> n <- c(8,11,22,6)
> m <- c(135.83,160.49,178.35,188.06)
> s <- c(19.59,12.28,15.01,9.81)
> sum(n*m)/sum(n)
[1] 168.1721
重み付け平均は168.1721と計算された。
> U <- s^2
> sqrt((sum((n-1)*U)+sum(n*(m-sum(n*m)/sum(n))^2))/(sum(n)-1))
[1] 22.39771
統合した標準偏差は、22.39771と計算された。
StatsToDoのプログラムでやってみる
オンラインで無料で提供されているプログラムが下記のリンク先にある。
これを使ってみる。
Javascript Programに上記のデータを入力する。
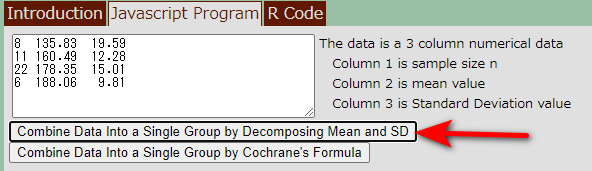
入力し終わったら、赤矢印のボタンをクリックする。
すると以下のように結果が出力される。
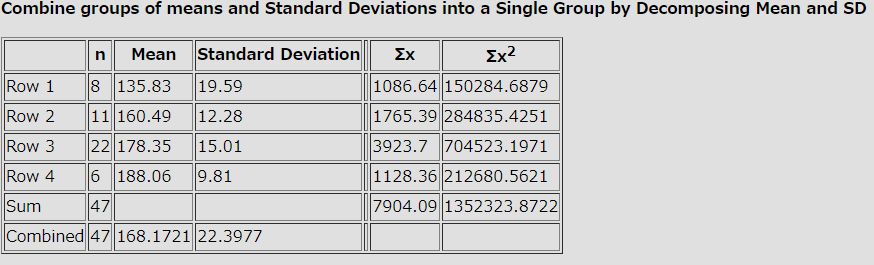
上記 R で計算した結果と同じ結果が得られる。
プールした分散の平方根
プールした分散を用いる方法もあると思う。
数式で表すと以下のようになる。
$$ \frac{(n_1 – 1) U_1 + (n_2 – 1) U_2}{n_1 – 1 + n_2 – 1} $$
n, U は各群のサンプルサイズと不偏分散である。
これはt検定の時に用いられる分散の統合方法である。
24-3. 2標本t検定とは | 統計学の時間 | 統計WEB
このプールした分散の平方根を取ることでもプールした標準偏差になると思う。
こちらは、自由度を重みにした重み付け不偏分散から計算された値と言える。
2群から4群に拡張して考え、統計ソフトRで計算すると以下のようになる。
> sqrt(sum((n-1)*U)/sum(n-1))
[1] 14.79067
4群のちょうど真ん中あたりの値になっている。
さきほどの計算結果とは若干異なる結果になる。
いずれにしてもどのように計算をしたかを明記すれば、どちらの方法でも問題ないと思う。
まとめ
連続データの層別解析要約値を統合したいときにどうすればよいか、説明した。
統合した平均と標準偏差の計算方法を提示し、無料で使えるOnlineサービスも紹介した。
標準偏差の統合には、2つの方法が考えられるが、どちらの方法を使ったのかを明記すれば、どちらでもよいだろう。
参考サイト
重み付け平均
https://staff.aist.go.jp/t.ihara/weight.html
群ごとの平均値・不偏分散を統合する方法
群ごとの平均値・不偏分散を統合する方法とは何? わかりやすく解説 Weblio辞書
プールした分散
t検定









コメント