ウェルチの t 検定は、2 群が等分散でも等分散でなくても使える t 検定
R と SPSS での実行方法
ウェルチの t 検定とは?
ウェルチ (Welch) の t 検定は、二つのサンプルの母分散が等分散とは仮定できないときにも適切に比較できる平均値の差の検定だ。
等分散の時でも使えるし、等分散ではなくても使える。
等分散の時は、ほぼ同じ結果になる。
だから、いつでもウェルチ検定を使えばいい。
等分散性の検定を事前に実施する必要はない。
ウェルチの t 検定を R で実行する
R でウェルチの t 検定を行う方法には、t.test()を使う。
t 検定の標準仕様がウェルチの t 検定になっている。
グループ1が4から14の11個のデータ、グループ2が1から11のそれぞれ3倍で11個のデータだとしよう。
X1 <-seq(1:11)+3
X2 <- seq(1:11)*3
データは、こんなふうに準備する。
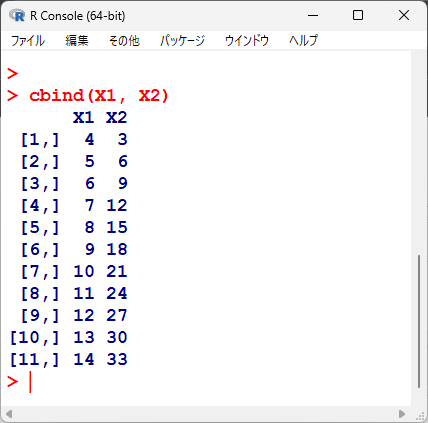
その時のウェルチの t 検定は、以下のように実施する。
t.test(X1,X2)
結果は、以下の通りで、p値が0.01453で統計学的有意に異なる。
> t.test(X1,X2)
Welch Two Sample t-test
data: X1 and X2
t = -2.846, df = 12.195, p-value = 0.01453
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-15.877804 -2.122196
sample estimates:
mean of x mean of y
9 18
ウェルチの t 検定を改めて作った関数で実施する
R のfunction()を使い、関数を改めて作って実施してみる。
変数は平均値、標準偏差、サンプルサイズを代入する形にする。
welch.t.test <- function (N1, X1bar, s1, N2, X2bar, s2,
alternative=c("two.sided","one.sided"))
{
data.name <- sprintf("\nN1=%s, X1bar=%s, SD1=%s\nN2=%s, X2bar=%s, SD2=%s", N1,X1bar,s1,N2,X2bar,s2)
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
estimate <- X1bar-X2bar
tstat <- abs(estimate)/sqrt(s1^2/N1+s2^2/N2)
names(tstat) <- "t"
df<-(s1^2/N1+s2^2/N2)^2/(s1^4/(N1^2*(N1-1))+s2^4/(N2^2*(N2-1)))
names(df) <- "df"
pval <- pt(q=tstat, lower.tail=F, df=df)*tside
METHOD <- "Welch t-test"
structure(list(statistic=tstat, parameter=df, p.value=pval,
estimate=estimate, alternative=alternative, data.name=data.name,
method=METHOD), class="htest")
}
グループ1とグループ2のサンプルサイズ、平均値、標準偏差を計算する。
X1 <-seq(1:11)+3
(N1 <- length(X1))
(X1bar <- mean(X1))
(s1 <- sd(X1))
X2 <- seq(1:11)*3
(N2 <- length(X2))
(X2bar <- mean(X2))
(s2 <- sd(X2))
さきほど作った関数に代入する。
welch.t.test(N1=11, X1bar=9, s1=3.316625, N2=11, X2bar=18, s2=9.949874)
結果はt.test()と同じ結果になる。
> welch.t.test(N1=11, X1bar=9, s1=3.316625, N2=11, X2bar=18, s2=9.949874)
Welch t-test
data:
N1=11, X1bar=9, SD1=3.316625
N2=11, X2bar=18, SD2=9.949874
t = 2.846, df = 12.195, p-value = 0.01453
alternative hypothesis: two.sided
sample estimates:
[1] -9
一人一人のデータがある場合は、t.test()を使えばよいが、人数、平均値、標準偏差だけが得られている場合は、今回自作の関数を使うと計算できる。
先行研究から人数、平均値、標準偏差という要約値しか得られない場合にどんな条件であれば、統計学的に有意になるかなどを検討する際に役立つ。
例えばグループ1の標準偏差が3倍(つまり同じ)になったら、どうなるか?
> welch.t.test(N1=11, X1bar=9, s1=3.316625*3, N2=11, X2bar=18, s2=9.949874)
Welch t-test
data:
N1=11, X1bar=9, SD1=9.949875
N2=11, X2bar=18, SD2=9.949874
t = 2.1213, df = 20, p-value = 0.04658
alternative hypothesis: two.sided
sample estimates:
[1] -9
先ほどに比べ、p値が3倍以上になっていて、0.05近くになっている。
このように簡単に架空の条件での結果を確認することができる。
これは、サンプルサイズ計算の際に役に立つ。
ウェルチの t 検定を SPSS でも実行してみる
SPSSでも計算してみた。
SPSSは以下のようにグループを縦方向に積み重ねて並べないと計算できない。
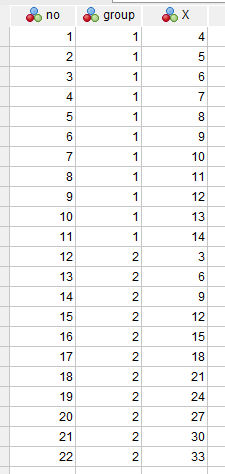
検定変数に目的変数Xを入れて、グループ変数にgroupを入れ、グループ1と2を認識させる。
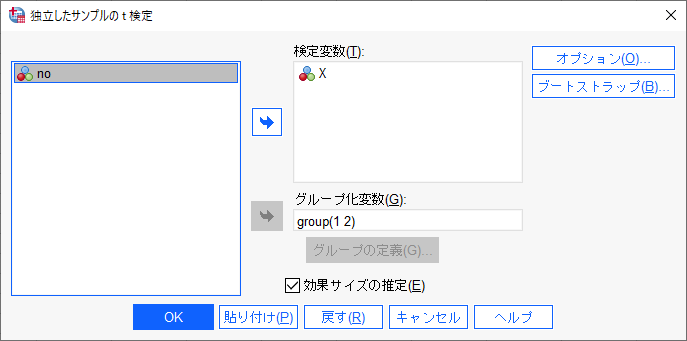
OKをクリックすると結果が出力される。
グループごとの統計量が計算される。
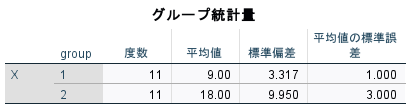
独立サンプルの検定の項に、検定結果が表示される。

等分散を仮定しないという行がウェルチの検定の結果だ。
さらに、要約の t 検定を使用してみる。
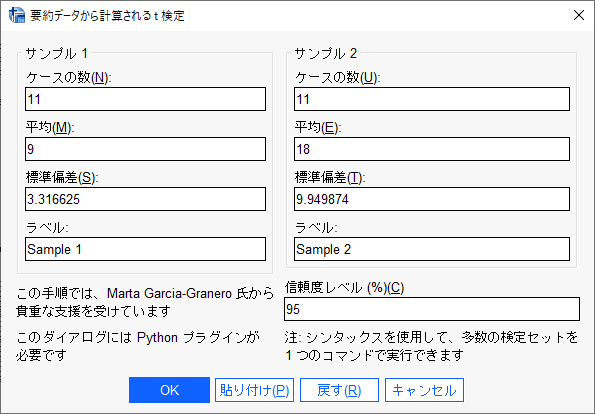
要約値(サンプルサイズ、平均値と標準偏差)を入力する。
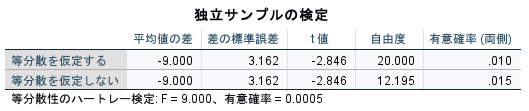
結果はRのt.test()と同じである。
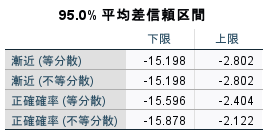
差の95%信頼区間は、正確確率で不等分散の行の結果が R の結果と一致していた。
まとめ
平均値の差の検定、いわゆる t 検定は、いつでもウェルチの t 検定を行えばよい。
等分散かどうかは気にしなくてよい。
R ではt.test()を使う。








コメント