非劣性マージンの決め方と R で非劣性検定を実行する方法

いままでの方法と比べて、格段にいいとか、際立っていいとか、じゃなくてもいい場合がある。

ダメじゃなければいい。

劣っていなければいい。

劣っていなければいいという検定方法が、非劣性（ひれっせい）検定だ。

じゃ、どういうときが劣っていないって言うのか？

非劣性マージンとは？劣っているとは？劣っていないとは？

劣っていないとはどういう状態を言うのか？

劣っているとはどう状態なのか？

実は誰もわからない。

非劣性検定で一番の問題はこの点だ。

「これ」以上劣っていたら、劣っているとする、という閾値（しきいち）を決める。

「これ」が非劣性マージンと呼ばれる幅だ。

だが、非劣性マージンは何が正解か誰もわからない。

非劣性マージンの決め方

参考になるスライドセットを見つけた。

www.slideshare.net

非劣性マージンを決めるときに必要なのは、標準治療とプラセボの効果の差と、保持率とか維持率と呼ばれる数値。

標準治療の効果と保持率＝維持率の掛け算で、非劣性マージンを決める。

では、保持率＝維持率とは何か？

標準治療のプラセボに対する効果の何割は効果があるか？ということ。

どんなに効果がなくても、標準治療の効果の半分は効果がある。

もしくは効果があってほしい、など。

新しい治療はまだ効果がよくわからないから、最悪でも標準治療の効果のどのくらいは効果がある、ということは実はわからない。

だから、保持率＝維持率は、あいまいだ。

主観なのだ。

もしくは願望。

どこまでいっても議論が尽きない理由がわかる。

非劣性試験の最大の弱点だ。

現実は、たくさん試験が行われていて、何らかの理屈をつけて適切な試験とみなされている。

その結果、効果は変わらないが、副作用が少ない治療法が生まれている。

どこまでも怪しさが残るが、全否定するほどでもない。

これが非劣性マージン、非劣性検定、非劣性試験だ。

非劣性マージンの決め方例

例 ：プラセボとの差の半分

出典：

非劣性試験に潜む問題点

割合の非劣性検定

Rのスクリプトを以下に示す。

non.inferior <- function(nA, nB, rA, rB, DELTA,
conf.level=0.9){
METHOD <- "Non-Inferiority Test (Dunnett-Gent)"
pB.star <- (rA+rB+nA*DELTA)/(nA+nB)
se.delta.hat <- sqrt(((pB.star-DELTA)*
(1-pB.star+DELTA))/nA+(pB.star*(1-pB.star))/nB)
pA.hat <- rA/nA
pB.hat <- rB/nB
STATISTIC <- (pA.hat-(pB.hat-DELTA))/se.delta.hat
names(STATISTIC) <- "Z"
PVAL <- 1-pnorm(STATISTIC)
se <- sqrt(pA.hat*(1-pA.hat)/nA+pB.hat*(1-pB.hat)/nB)
delta <- pA.hat-pB.hat
WIDTH <- qnorm(1-(1-conf.level)/2)
CINT <- c(delta - WIDTH*se, delta + WIDTH*se)
attr(CINT, "conf.level") <- conf.level
RVAL <- list(statistic=STATISTIC,
p.value=as.numeric(PVAL),
estimate=c(pA=pA.hat, pB=pB.hat, pBstar=pB.star),
conf.int=CINT, method=METHOD)
class(RVAL) <- "htest"
return(RVAL)
}
non.inferior(nA=128, nB=127,
rA=64+37, rB=57+39, DELTA=0.1)

Rコンソールにコピペすれば使える。

臨床的に意味のある最小の差（DELTA）が非劣性マージンだ。

どんなに最悪でもそこは下回らないという限界点。

• pA.hat: 試験薬の有効率
• pB.hat: 標準薬の有効率

• pB.star: 帰無仮説(H0:pA=pB-DELTA)の下でのpB

• DELTA: 臨床的に意味のある最小の差→10%（0.1）とする

• rA: 試験薬群の有効症例数→64人と37人とする
• nA: 試験薬群のサンプルサイズ→128とする
• rB: 標準薬群の有効症例数→57人と39人とする
• nB: 標準薬群のサンプルサイズ→127とする

STATISTICSが検定統計量で、漸近的に正規近似できる検定統計量だ。

non.inferiorが自作関数名だ。

non.inferior()で使う。

結果は以下の通り。

> non.inferior(nA=128, nB=127, rA=64+37, rB=57+39, DELTA=0.1)
Non-Inferiority Test (Dunnett-Gent)
data:
Z = 2.5561, p-value = 0.005293
90 percent confidence interval:
-0.05314985  0.11946383
sample estimates:
pA        pB    pBstar
0.7890625 0.7559055 0.8227451

p値は片側で出している。

非劣性は最低この点は下回らないという仮説で、片側しか興味がないため、興味がある側の片側p値を出す。

90%信頼区間を出力しているのも、下限5%のラインを見るためだ。

非劣性マージンｰ10%（-0.1)よりも、信頼区間の下限が大きく-0.05のため、非劣性と言えるわけだ。

ただし、有効性100%の場合は計算できない。

> non.inferior(nA=188, nB=91, rA=188, rB=91, DELTA=0.1)
Non-Inferiority Test (Dunnett-Gent)
data:
Z = NaN, p-value = NA
90 percent confidence interval:
0 0
sample estimates:
pA       pB   pBstar
1.000000 1.000000 1.067384
Warning message:
In sqrt(((pB.star - DELTA) * (1 - pB.star + DELTA))/nA + (pB.star *  :
NaNs produced

割合の非劣性検定を最尤推定量で行うには？

正規近似は100%を超えてしまうときは使えない。

現実には、両群とも有効率100%がありうる。

有効率100%を非劣性検定するには、最尤推定量に基づく検定を利用する必要がある。

pB.star: 帰無仮説(H0:pA=pB-DELTA)の下でのpB

の計算が前節の正規近似と異なり、ややこしい。

non.inferior.likelihood <- function(nA, nB, rA, rB, DELTA,
conf.level=0.9){
METHOD <- "Non-Inferiority Test (Likelihood Method)"
pA.hat <- rA/nA
pB.hat <- rB/nB
a <- nA+nB
b <- -1*(nB+nA+rB+rA+DELTA*(nA+2*nB))
c <- nB*DELTA^2+DELTA*(2*rB+nA+nB)+rB+rA
d <- -rB*DELTA*(1+DELTA)
v <- b^3/(27*a^3)-(b*c)/(6*a^2)+d/(2*a)
u <- sign(v)*sqrt(b^2/(9*a^2)-c/(3*a))
w <- (pi+acos(v/u^3))/3
pB.star <- 2*u*cos(w)-b/(3*a)
se.delta.hat <- sqrt(((pB.star-DELTA)*
(1-pB.star+DELTA))/nA+(pB.star*(1-pB.star))/nB)
STATISTIC <- (pA.hat-(pB.hat-DELTA))/se.delta.hat
names(STATISTIC) <- "Z"
PVAL <- 1-pnorm(STATISTIC)
se <- sqrt(pA.hat*(1-pA.hat)/nA+pB.hat*(1-pB.hat)/nB)
delta <- pA.hat-pB.hat
WIDTH <- qnorm(1-(1-conf.level)/2)
CINT <- c(delta - WIDTH*se, delta + WIDTH*se)
attr(CINT, "conf.level") <- conf.level
RVAL <- list(statistic=STATISTIC,
p.value=as.numeric(PVAL),
estimate=c(pA=pA.hat, pB=pB.hat, pBstar=pB.star),
conf.int=CINT, method=METHOD)
class(RVAL) <- "htest"
return(RVAL)
}
non.inferior.likelihood(nA=128, nB=127,
rA=64+37, rB=57+39, DELTA=0.1)

結果は以下の通り。

p値がほんの少し大きくなり、帰無仮説の下でのpB（pBstar）は、ほんの少し小さく見積もられている。

> non.inferior.likelihood(nA=128, nB=127, rA=64+37, rB=57+39, DELTA=0.1)
Non-Inferiority Test (Likelihood Method)
data:
Z = 2.5181, p-value = 0.0059
90 percent confidence interval:
-0.05314985  0.11946383
sample estimates:
pA        pB    pBstar
0.7890625 0.7559055 0.8129256

最尤推定量に基づく方法なら有効性100%でも検定できる。

> non.inferior.likelihood(nA=188, nB=91, rA=188, rB=91, DELTA=0.1)
Non-Inferiority Test (Likelihood Method)
data:
Z = 4.5704, p-value = 2.434e-06
90 percent confidence interval:
0 0
sample estimates:
pA     pB pBstar
1      1      1

最尤推定量に基づく方法で検定しておけば、いつでも問題ない。

R の TOSTER パッケージを使った方法（twoprop_test 関数）

R の TOSTER パッケージを使うと、以下のように簡単に計算できる

library(TOSTER)
twoprop_test(p1=(64+37)/128, p2=(57+39)/127,
n1=128, n2=127, null=-0.1,
alternative="greater")

結果は、以下のように出力される

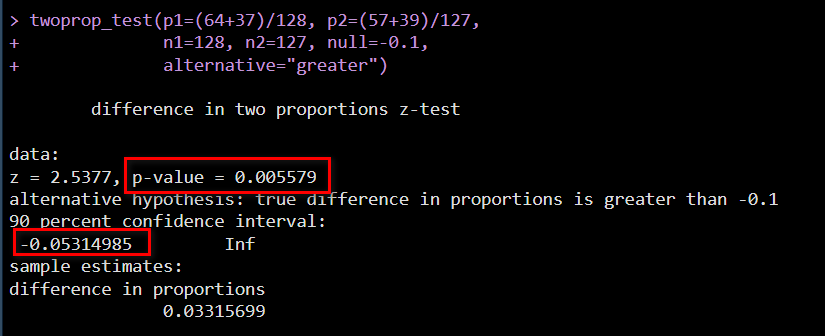
p1 のほうが大きい（greater）という対立仮説で、帰無仮説（null）には、0 の代わりに、-0.1 とする

これによって、-0.1 が棄却されれば、少なくとも ‐0.1 よりも小さいことはないと言えることになり、非劣性マージン ‐0.1 よりは大きいことが示されたことになる

P 値は、上記のスクリプトによる結果と同様の、0.005579 となり、差の 90 ％ 信頼区間の下限を見ると、-0.1 よりも大きい、約 ‐0.053 となっていて、結果が整合していることがわかる

非劣性検定　割合の場合　エクセル計算機

母比率の非劣性検定（最尤推定量に基づく方法）を計算するエクセル計算機を作ったので、よければどうぞ。

割合の非劣性検定 計算機【エクセル計算機】 | TKER SHOP

使い方解説動画も、よければどうぞ。

平均値の非劣性検定

変化量の平均値のような場合、非劣性検定はどうやるか？

帰無仮説 $ H_0 $ と対立仮説 $ H_1 $ は以下の通りだ。

$$ H_0: \mu_A \leqq \mu_B – \Delta $$

$$ H_1: \mu_A > \mu_B – \Delta $$

臨床上意味のある最小の差を引いて、同じかそれよりも劣る、が帰無仮説 $ H_0 $

対立仮説 $ H_1 $ は臨床上意味のある最小の差を引くと、少なくともそのレベルは上回る効果がある。

non.inferiority.mean <- function(
nA, xbarA, sdA, nB, xbarB, sdB, Delta, conf.level=.9){
data.name <- sprintf("\nN_A = %s, Mean_A = %s, SD_A = %s\n
N_B = %s, Mean_B = %s, SD_B = %s\nDelta = %s",
nA, xbarA, sdA, nB, xbarB, sdB, Delta)
METHOD <- "Non-inferiority test (Mean)"
df <- nA-1+nB-1
names(df) <- "df"
SE <- sqrt((1/nA+1/nB)*(((nA-1)*sdA^2+(nB-1)*sdB^2)/df))
STATISTIC <- (xbarA - (xbarB - Delta))/SE
names(STATISTIC) <- "T"
PVAL <- 1 - pt(STATISTIC, df)
delta <- xbarA - xbarB
WIDTH <- qt(1-(1-conf.level)/2, df)
CINT <- c(delta-WIDTH*SE, delta+WIDTH*SE)
attr(CINT, "conf.level") <- conf.level
RVAL <- structure(list(statistics=STATISTIC, parameter=df,
p.value=as.numeric(PVAL), data.name=data.name,
conf.int=CINT, method=METHOD))
class(RVAL) <- "htest"
return(RVAL)
}
non.inferiority.mean(nA=46, xbarA=34.5, sdA=32.02,
nB=44, xbarB=29.7, sdB=28.42, Delta=7)

結果は以下の通り。

平均の差は4.8で、これはどんなに悪くても-7よりは小さくはならないはず、というのが証明したい仮説だ。

計算結果、片側p値は0.034で、有意水準片側5％とすると統計学的有意。

90%信頼区間（片側5％）の下限は-5.8で、-7より大きいため、最悪でも-7よりは悪くない。

よって、非劣性が証明された。

> non.inferiority.mean(nA=46, xbarA=34.5, sdA=32.02, nB=44, xbarB=29.7, sdB=28.42, Delta=7)
Non-inferiority test (Mean)
data:
N_A = 46, Mean_A = 34.5, SD_A = 32.02
N_B = 44, Mean_B = 29.7, SD_B = 28.42
Delta = 7
T = 1.8459, df = 88, p-value = 0.03413
90 percent confidence interval:
-5.826446 15.426446

R の TOSTER パッケージを使った方法（tsum_TOST 関数）

R の TOSTER パッケージの tsum_TOST を使うと、同じ計算が簡単にできる

install.packages("TOSTER") # インストールは 1 回だけ実行
library(TOSTER)
tsum_TOST(m1=34.5, sd1=32.02, n1=46,
m2=29.7, sd2=28.42, n2=44, eqb=-7)

結果は以下のように表示される

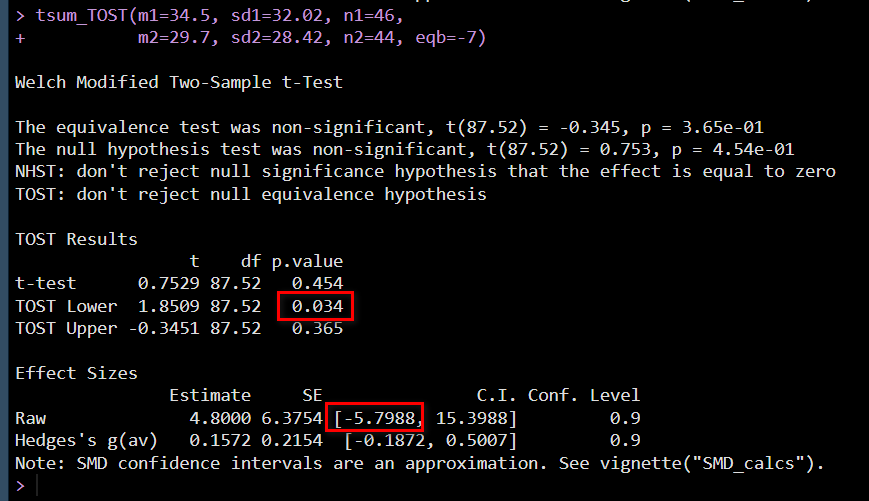
TOST Lower の p.value が片側 p 値である

Effect Sizes の Raw 行の C.I. 下限値が 片側 5 ％ の下限値である

ともに、上記の計算と一致している（下限値は少しずれている。計算式違いのためと思われる）

非劣性検定　平均値の場合　エクセル計算機

平均値の非劣性検定を計算するエクセル計算機を作ったので、よければどうぞ。

平均値の非劣性検定 計算機【エクセル計算機】 | TKER SHOP

使い方解説動画も、よければどうぞ。

まとめ

非劣性検定を割合の場合と平均値の場合に分けて紹介した。

割合の場合は最尤推定量の基づく方法がベターだ。

非劣性検定は、非劣性マージンの設定が問題となる。

非劣性マージンが適切に設定され、サンプルサイズが適切に見積もられてはじめて、非劣性検定が意味を成す。

参考書籍

丹後俊郎著　無作為化比較試験　朝倉書店
6. 非劣性の評価