R で二項分布のグラフを書いてみた
二項分布のグラフの前に 二項とは?
二項とは、0か1か、YesかNoか、表か裏か、など二つに一つが選ばれること。
二項分布は、二項の場合の分布という意味である。
二項分布のグラフを書いてみる
たとえば、10例で、確率5割のこと、10回コインを投げて、表裏どちらも確率5割、10回挑戦してみて、成功確率は五分五分。
このとき0回から10回までの、起きる確率、表の確率、成功確率をグラフ描画すると5回が最も確率が高くなる。
R での二項分布のグラフを書くスクリプトは以下の通り。
plot(x=0:10, y=dbinom(x=0:10, size=10, prob=0.5), type="h")
二項分布のグラフは以下の通り。
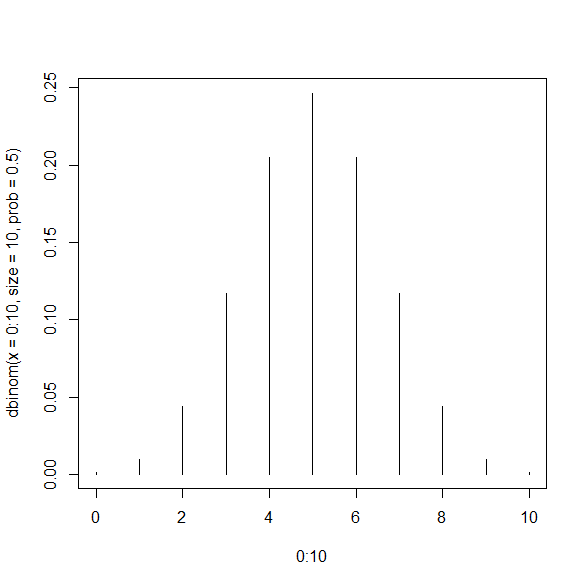
このとき、0 から 10 までの発生確率 y は、以下のような数値になっていて、これが Y 軸の高さになっている。
> x <- 0:10
> y <- dbinom(x=0:10, size=10, prob=0.5)
> cbind(x, y)
x y
[1,] 0 0.0009765625
[2,] 1 0.0097656250
[3,] 2 0.0439453125
[4,] 3 0.1171875000
[5,] 4 0.2050781250
[6,] 5 0.2460937500
[7,] 6 0.2050781250
[8,] 7 0.1171875000
[9,] 8 0.0439453125
[10,] 9 0.0097656250
[11,] 10 0.0009765625人数や試行の数を5、20、50の3パターンにする。それぞれ、成功確率を0.3、0.5、0.7とする。
全部で9パターンのグラフを描画する。
R のスクリプトは以下の通り。
layout(matrix(1:9,nr=3))
plot(0:5, dbinom(0:5, 5, 0.3), type="h", ylim=c(0,0.4))
plot(0:5, dbinom(0:5, 5, 0.5), type="h", ylim=c(0,0.4))
plot(0:5, dbinom(0:5, 5, 0.7), type="h", ylim=c(0,0.4))
plot(0:20, dbinom(0:20, 20, 0.3), type="h", ylim=c(0,0.4))
plot(0:20, dbinom(0:20, 20, 0.5), type="h", ylim=c(0,0.4))
plot(0:20, dbinom(0:20, 20, 0.7), type="h", ylim=c(0,0.4))
plot(0:50, dbinom(0:50, 50, 0.3), type="h", ylim=c(0,0.4))
plot(0:50, dbinom(0:50, 50, 0.5), type="h", ylim=c(0,0.4))
plot(0:50, dbinom(0:50, 50, 0.7), type="h", ylim=c(0,0.4))
グラフはこのように書ける。
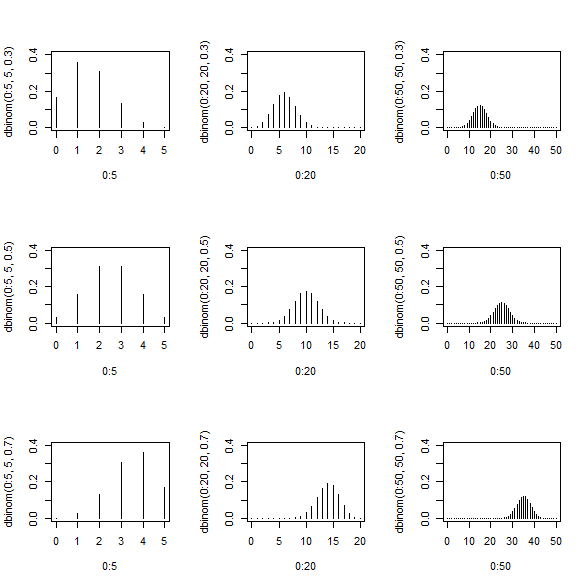
人数や試行が大きくなると、正規分布に近づいていく。
正規分布に近づいていく性質を使って、母比率の推定は正規近似で行われていた。
二項分布はどう使うか?
二項分布は母比率の区間推定に使える。
人数や試行回数が大きくなると正規分布に近づくために、これまでは正規近似が用いられていた。
しかし、コンピューターを使えるようになって、近似を使う意味合いはなくなった。
R なら、binom.test()で簡単に計算できる。
50例中、35例がYesだったとする。
このときの95%信頼区間は、0.5539177~0.8213822と計算される。
> binom.test(35, 50)
Exact binomial test
data: 35 and 50
number of successes = 35, number of trials = 50, p-value = 0.0066
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.5539177 0.8213822
sample estimates:
probability of success
0.7 ちなみに正規近似で95%信頼区間を求めると、0.5729775~0.8270225と計算される。
> 0.7+c(-1, 1)*1.96*sqrt(0.7*(1-0.7)/50)
[1] 0.5729775 0.8270225
しかし、現代では、この計算方法は使用しなくてもよくなった。
まとめ
二項分布は、二項のうち一方が起きる回数の確率を表した分布。
試行回数が大きくなると正規分布に近づく。
R なら、二項分布を使った母比率の区間推定が binom.test() 関数で計算できる。









コメント