ガンマ分布とはどんな分布か簡単に解説しながら、R でガンマ分布のグラフを描く方法を紹介
目次
ガンマ分布とは?
ガンマ分布は、ある期間ごとに1回起こることが、何回か起こるまでの時間の分布。
たまにしかおきない、まれにしかおきない、という感じがポアソン分布をほうふつとさせる。
ポアソン分布については、こちらを参照。
あわせて読みたい

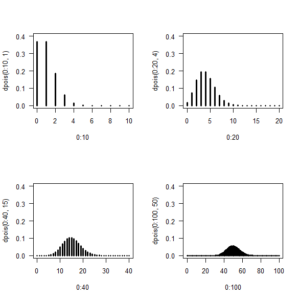
R でポアソン分布のグラフを描く方法
R を使ったポアソン分布の書き方の解説 ポアソン分布とは? ポアソン分布は、数学者ポアソンが発表した、離散確率分布。 離散とは、離れているということ。 0回、1回、2…
ガンマ分布はどんな時に使う?
ガンマ分布は、ベイズ統計学に登場する。
尤度を計算するデータを取ってくる母集団がポアソン分布している場合の共役事前分布なのだ。
共役事前分布の読み方は、きょうやくじぜんぶんぷ。
共役事前分布はこちらも参照のこと。
あわせて読みたい

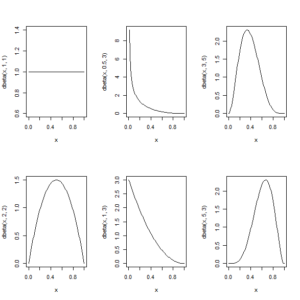
R でベータ分布のグラフを描く方法
ベータ分布は、ベイズ統計学で二項分布の共役事前分布(きょうやくじぜんぶんぷ)として登場する分布。 ベータ分布の前に共役事前分布って何? ベータ分布は、二項分布…
$$ ガンマ分布 \times ポアソン分布データからの尤度 \propto ガンマ分布 $$
$ \propto $ は、「比例する」の意味。
共役事前分布がガンマ分布なら、事後分布もガンマ分布になる。
事後分布が次の共役事前分布になる。
R でガンマ分布はどう描く?
dgamma()がガンマ分布の確率を計算する。
curve()と組み合わせると曲線が描ける。
0以上の値xについて分布を描く。
shapeは、何回起こるかの定義で、形状母数という。
scaleは、ある期間 にあたり、尺度母数という。
scaleの逆数がrateで、ある期間に一回なので率になる。
dgamma()では、0以上の値xと、shapeとrateまたはscaleを指定して、確率を計算し分布を描くことができる。
x <- seq(0,8,0.5)
curve(dgamma(x, shape=1, rate=1),from=0,to=8, lwd=3)
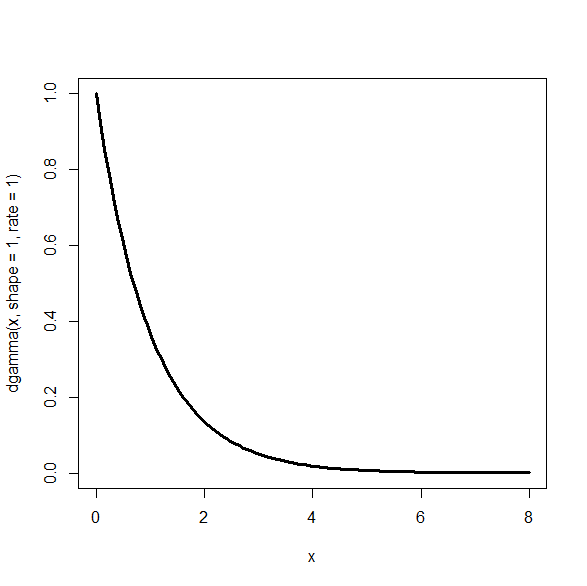
何回起こるかのshapeを1,2,3,4と変えると、形状が変わることがわかる。
layout(matrix(1:4,nr=2))
curve(dgamma(x, 1, 1), 0, 8, lwd=3, ylim=c(0,1))
curve(dgamma(x, 2, 1), 0, 8, lwd=3, ylim=c(0,1))
curve(dgamma(x, 3, 1), 0, 8, lwd=3, ylim=c(0,1))
curve(dgamma(x, 4, 1), 0, 8, lwd=3, ylim=c(0,1))
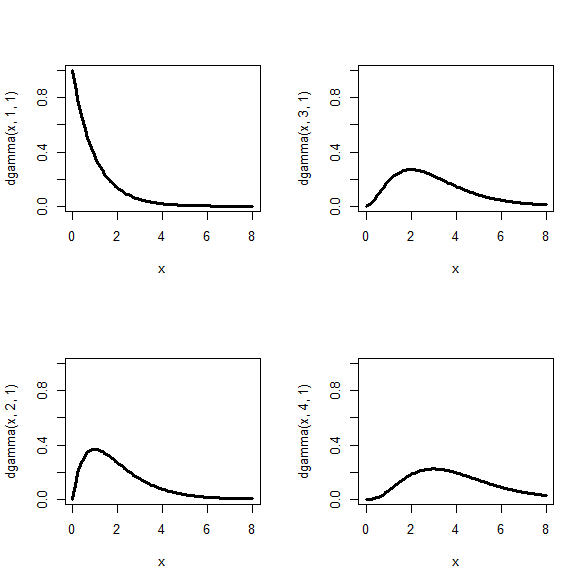
まとめ
ガンマ分布について簡単に解説し、R でグラフを書く方法を解説した。
参考になれば。
参考書籍











コメント