t分布とは何か?t検定とどう関係するのか?
t分布とはいったい何なのか?
t検定とはよく聞くが、それとt分布は関係あるのか?
t分布は要するに何なのか?
実は、t分布は標準正規分布の代わりだ。
どんなときに代わりとして使うか。
2つ条件がある。
- 母分散が未知の場合。
- サンプルサイズが小さい場合。
統計学の演習課題では、母分散がわかっていることが多いが、現実的にはわからない。
ゆえに母分散は未知と考えるほうが自然だ。
標準正規分布であれば、p=0.975のクォンタイルが1.96である。
しかし、t分布では、サンプルサイズが500を超えないと、p=0.975のクォンタイルが1.96にならない。
サンプルサイズが小さいときは、1.96 よりも大きくなってしまう。
> qt(p=0.975,df=400)
[1] 1.965912
> qt(p=0.975,df=500)
[1] 1.96472
> qt(p=0.975,df=600)
[1] 1.963926
よって、どんなときも、現実の統計学では、標準正規分布を使いたい場面では、t分布を使うのが適切なのだ。
クォンタイルについては、こちらを参照。

t分布はどんな形をしているか?
標準正規分布をなだらかにした形をしている。
実線が自由度8のt分布。
点線が標準正規分布。
各群5例で、t検定をするとすれば、自由度8のt分布を使う。
n1 <- 5
n2 <- 5
df <- n1+n2-2
curve(dt(x, df), -4, 4, las=1, xlab="t")
curve(dnorm(x), -4, 4, lty=2, add=T)
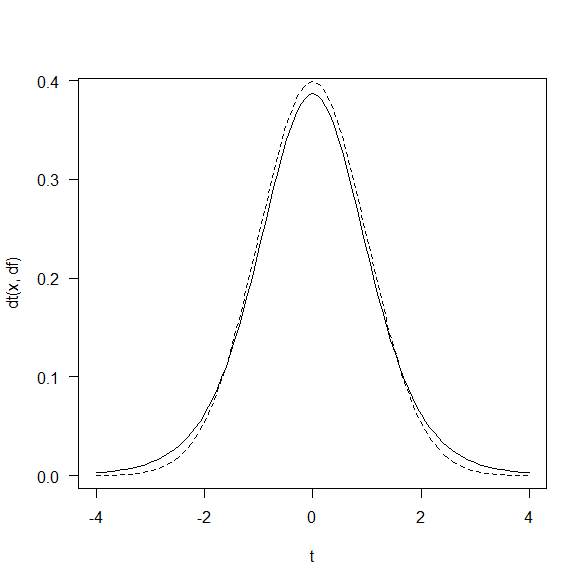
ほぼ同じように見えるが、サンプルサイズが小さい検定の場合は、 t分布を使ったほうがよい。
t検定とt分布はどう関係する?
t検定は、独立2群の平均値の差の検定とも呼ばれる。
t検定では、各群の母平均が等しいという帰無仮説から物事を考え始める。
大事なのは検定統計量tを計算することだ。
tはこんな式で計算される。
$$ t = \frac{\overline{x_1} – \overline{x_2}}{\sqrt{U_e \left( \frac{1}{n_1 – 1} + \frac{1}{n_2 – 1} \right)}} $$
ここで、$ \overline{x_1} $ と $ \overline{x_2} $ は、それぞれの群の平均値。
$ n_1 $ と $ n_2 $ はそれぞれの群のサンプルサイズ。
$ U_e $ は両群を合わせた分散の推定値。計算式は以下の通り。
$$ U_e = \frac{(n_1 – 1) U_1 + (n_2 – 1) U_2}{n_1 – 1 + n_2 – 1} $$
$ U_1 $ と $ U_2 $ はそれぞれの群の不偏分散。
分子は、平均値の差、分母は、平均値の差の標準誤差。
言葉で書けば、
$$ t = \frac{平均値の差}{標準誤差} = \frac{効果}{ノイズ} $$
と言える。
つまり、サンプルサイズの小ささやデータのばらつきなど、効果を検出するための「ノイズ」を超えて、効果が大きいと判断できれば、母集団でも違いがあると判断出来る。
結論は、統計学的有意な差がある(統計学的有意差がある)となる。
統計学的有意と判断する閾値(しきいち)は、絶対値で2くらいだ。
統計学的有意の閾値の2くらいとは?
検定では、慣例として、5%未満をまれなこととしている。
20回に1回はまれ。
まれに間違うことを許容している。
5%未満のことが起きたとすれば、まれなことが起きたとして、仮説が間違っていたと考える。
つまり、帰無仮説を捨てて、母平均に差があると結論付ける。
この5%をどうやって判断しているかというと、先ほどの検定統計量より絶対値が大きな値になる確率が5%未満かどうかで判断している。
絶対値が大きくなる条件は3つ。
- 平均値の差が大きくなること
- 各群の分散が小さくなること
- 各群のサンプルサイズが大きくなること
サンプルサイズが両群合わせて500を超えるなら、97.5パーセンタイルや2.5パーセンタイルの時のクォンタイルは±1.96だ。
サンプルサイズが小さくなると、2に近づき、2を超えてくる。
> qt(p=0.975, df=100)
[1] 1.983972
> qt(p=0.975, df=50)
[1] 2.008559
> qt(p=0.975, df=20)
[1] 2.085963
> qt(p=0.975, df=10)
[1] 2.228139
このクォンタイルのことを閾値と呼び、2くらいと表現した。
「閾値より大きい」を図に表すとどうなるか?
自由度8のt分布を使って、上側2.5%、下側2.5%のところを塗りつぶす。
これが閾値よりも絶対値で大きいときの確率を表している。
パーセンタイルでいうと、上側は97.5パーセンタイル、下側は2.5パーセンタイル。
n1 <- 5
n2 <- 5
df <- n1+n2-2
curve(dt(x, df), -4, 4, las=1, xlab="t")
arrows(qt(0.975,df),0,qt(0.975,df),dt(qt(0.975,df),df),0)
arrows(qt(0.025,df),0,qt(0.025,df),dt(qt(0.025,df),df),0)
xvalu <- seq(qt(0.975,df),4,length=20)
dvalu <- dt(xvalu, df)
polygon(c(xvalu, rev(xvalu)), c(rep(0,20), rev(dvalu)),col="skyblue")
xvall <- seq(-4, qt(0.025,df),length=20)
dvall <- dt(xvall, df)
polygon(c(xvall, rev(xvall)), c(rep(0,20), rev(dvall)),col="skyblue")
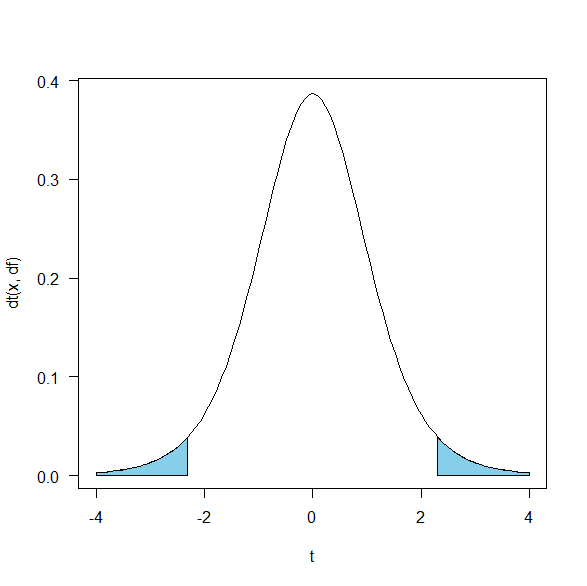
塗りつぶした図がこちら。
これがp値が0.05のときの状態。
つまり、p値は割合=確率=面積なのだ。
もしt値が1.5と計算されたとしよう。
するとt=1.5は上側の青い面積には入らない。
arrows(1.5, 0, 1.5, dt(1.5, df), 0)
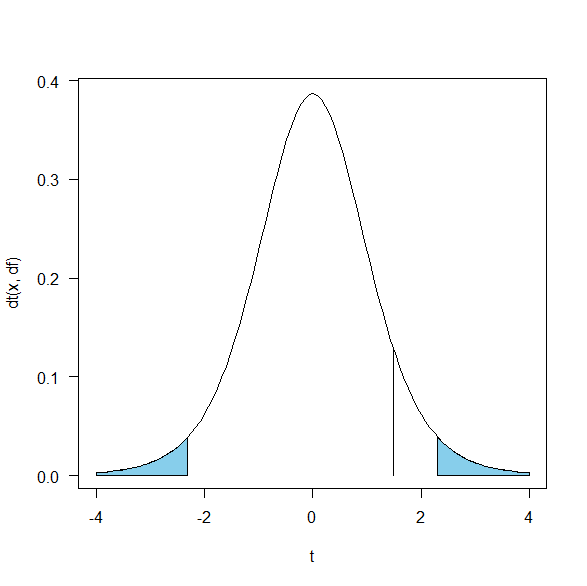
ゆえに統計学的有意でない。
ちなみに自由度8でt=1.5の場合、91.4パーセンタイル。
上側8.6パーセント。
これは100から91.4を引いて計算してる。
両側検定であれば、2倍の0.172
これがp値となる。
> pt(1.5, df=8)
[1] 0.9139984
> 1-pt(1.5, df=8)
[1] 0.08600165
> (1-pt(1.5, df=8))*2
[1] 0.1720033
R で t 分布をずらして一度に表示させる方法
帰無仮説のt分布と対立仮説のt分布の説明の時に、t分布をずらして2つ並べて表示したいことがある。
そんなときは、以下のように、描画範囲を広げて、例えば-4から4を-4から7などにして、平均をずらすために、クォンタイルから例えば3を引いてx-3などとして描画すると、2つのt分布を並べることができる。
curve(dt(x, 8), -4, 7, las=1, xlab="t")
curve(dt(x-3, 8), -4, 7, lty=2, add=T)
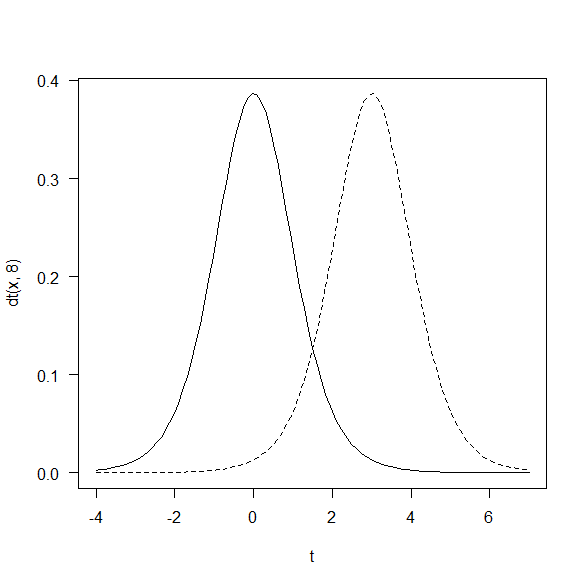
自由度8のt分布をクォンタイル3だけずらして2つ並べて描画した。
まとめ
t分布は、母分散がわからないとき、サンプルサイズが小さいときの、標準正規分布の代替分布。
独立2群の平均値の差の検定である、t検定で使用される。
標準正規分布で閾値だった1.96から少し大きめで2くらいだが、これはサンプルサイズから計算される自由度による。
t検定から計算されるp値は、いまよりももっと効果がある場合の確率の合計で、図で表すと面積になる。
参考書籍









コメント