-

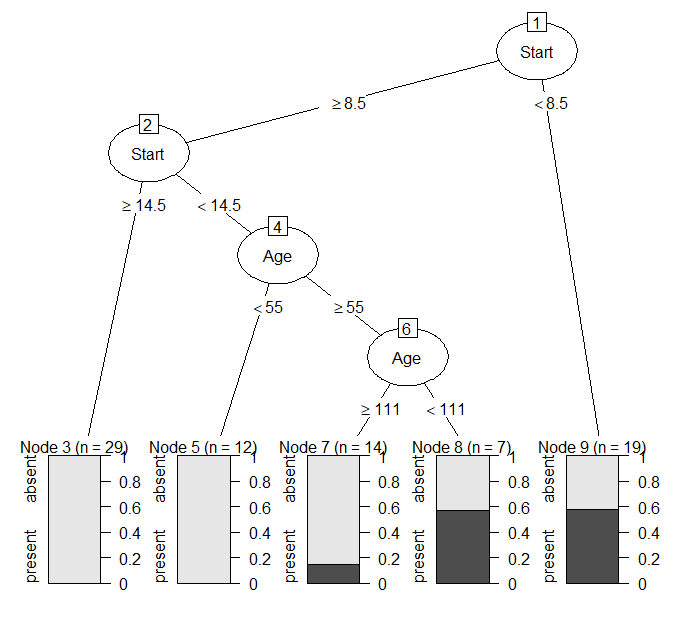
R partykit で決定木分析を実行する方法
決定木分析をRで行う方法を紹介。 難しいプログラムが組めなくてもすぐに使える。 決定木分析のRパッケージの準備 決定木分析のパッケージrpartときれいな決定木の描画パッケージpartykitをインストールする。 インストールは初めの一回だけでOK。 install... -

決定木の過学習を防ぐ剪定(枝刈り)とは?
決定木には剪定(せんてい)という過程がある。 剪定とは何か? 簡単に紹介。 決定木の弱点 過学習 あるデータセットから、決定木を作ったとする。 決定木は、大きく茂らせれば茂らせるほど、きれいに分岐して、分類してくれる。 しかしながら、機械学習... -

機械学習の決定木分析に計算される Gini 不純度とは? わかりやすく解説
決定木の分岐(ノード)を作るときどのような計算をしているのか? Gini不純度を計算しているのだが、Gini不純度とは何か? 機械学習の決定木における Gini 不純度とは? Gini不純度とは、ある特徴でデータを2分割するときに、特徴の要素Aである確率とAで... -

機械学習による決定木分析 ごく簡単な解説
機械学習をする方法はさまざまある。 代表的な方法は決定木分析である。 そもそも決定木とは何か? 基本的なことをごく簡単に解説。 決定木とは何か? 決定木とは意思決定に使う、いくつもの枝分かれをする図のこと。 膨大なデータを使って、決定木のモデ... -

統計に必要なサンプル数が計算できるエクセルファイルのリンク集
標本の大きさの求め方。エクセルを使う方法。 サンプルサイズ計算をエクセルで行う方法。 なかなか探しても見つからないサンプルサイズ計算がここでは見つかる!! アンケート調査 アンケートは何人に取れば最適なのか? エクセルファイルで簡単に計算でき... -

R で分類課題を機械学習モデルで実行する方法
機械学習で、よりよく推測できるモデルを選ぶ。 統計ソフトRのISLRパッケージのWeeklyデータで基礎的な機械学習を行ってみた。 Rで機械学習を行うためデータの準備 ISLRパッケージのWeeklyデータは、S&P500指数の週当たりのリターンのデータ。 9つの変... -

R で重回帰分析を行う具体例 ― ISLR パッケージ Auto データセットを使った重回帰分析
R の ISLR パッケージの Auto データセットを使った分析例。 データの準備 最初の一回だけ、ISLRパッケージをインストール。 install.packages("ISLR") ISLRパッケージを呼び出して、解析開始。 library(ISLR) ISLRパッケージのAutoデータセットを用いて解... -

R で NNH Number Needed to Harm を計算する方法
有害必要数(Number Needed to Harm, NNH)は、1人の有害事象が起こる人が出現するのに、何かの影響を受けた人が何人必要かという数。 NNHを計算するにはどうやるか? 使えるシチュエーションは、 曝露Aを受ける人受けない人 処置Bを受ける人受けない人 介... -

R で罹患率比を求める方法
罹患率比の計算は、どうやるのか? R での計算の方法。 罹患・罹患率・罹患率比とは? 罹患(りかん)とは? 罹患とは病気にかかること。 病気にかかったことは、診断によってわかる場合と、発症によってわかる場合がある。 診断とは、外来の診察で下され... -

相関と回帰の違いは何か?
相関と回帰はどう違うか? 両方とも2つのデータの関係性を見ているわけで、とても似ている。相関と回帰の違いについて、まとめてみる。 相関と回帰の根本的な違いは? 相関は、相関係数が中心で、 データXとデータYの お互いの関係性を見る。 相関分析には...