正規性の確認は、検定は不要で、グラフで確認すればよい。
ヒストグラムが一番簡単な方法だが、もう一つグラフで確認する方法がある。
それがQQプロットだ。
QQプロットとは何か?
QQプロットの前に 正規性とは?
統計解析の検定において正規性が条件であるものが多い。
正規性とは、母集団においてデータが正規分布していることを言う。
母集団はそもそもつかみどころがなく、いわゆる母集団は無限母集団のため、無限であるがゆえにデータ全体はとらえられない。
つまり、母集団そのものの正規性を直接を調べることはできないので、母集団からのランダムサンプルを用いて、母集団のデータの正規性を推測することになる。
推測するには大きく分けて2種類ある。
QQプロットの前に 正規性を確認する方法
ひとつは、検定である。
検定は、サンプルサイズが大きくなればなるほど、意味のないずれを検出してしまい、グラフで確認すれば正規分布と言っていい分布をしているのに、正規分布ではないという結論になってしまう。
なので、検定はお勧めしない。
ということで、ここでは、紹介もしない。
もう一つは、グラフによる確認である。
グラフによる確認で充分である。
グラフによる確認には2つある。
ひとつは、なじみ深いヒストグラムである。
以下のように、左右にバランスよく裾を引いて、階級を細かくすれば、釣り鐘型に見える例のグラフである。
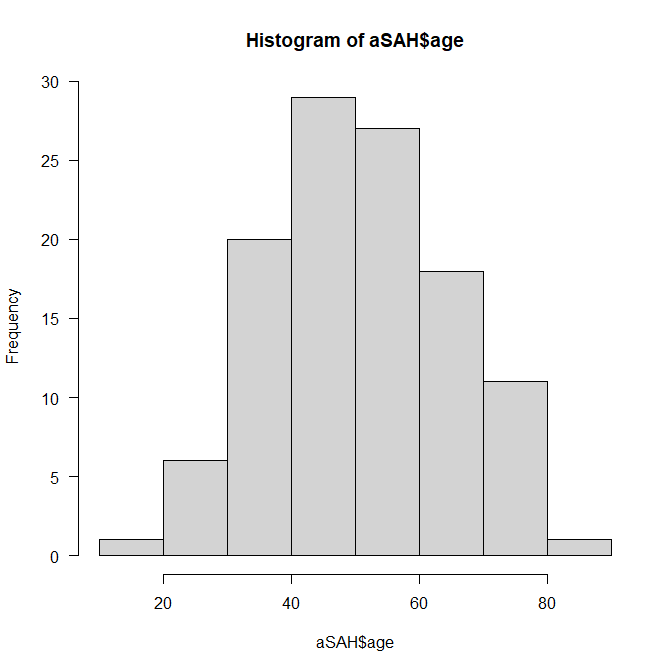
正規分布はこちらも参照のこと。
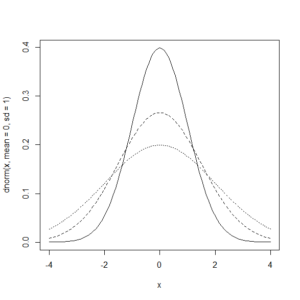
左右対称の釣り鐘型に見えれば、正規分布していると言ってよい。
もう一つは、この記事のタイトルにあるQQプロット(キューキュープロット)である。
QQプロットとは何か?
QQプロットとは?
QQプロットのQQとは、Quantile-Quantileの頭文字である。
Quantile(クォンタイル)は、日本語で言うと分位数と呼ばれる。
クォンタイルについては、こちらも参照のこと。

標準正規分布でいうところのZ値である。
平均をゼロとして、標準偏差で標準化したときに、平均ゼロからどのくらい離れているかをプラスとマイナスの数値で表現する。
±1.96の範囲が、標準正規分布の曲線下面積が95%であることは有名な話だ。
これが95%信頼区間の公式に1.96をよく見かけるゆえんである。
このクォンタイルをX軸にしたプロットである。
Y軸は、実際の値である。
では、X軸のクォンタイルはどこから計算されているのか?
それはY軸の実際の値からである。
- まず、Y軸の値を小さい順に並べる。
- Y軸の変数の中で最大値を100パーセンタイルとしたときに、小さいほうからパーセンタイル値を計算する。
- そのパーセンタイル値に対応するクォンタイル値を標準正規分布を用いて計算してX軸の変数とする。
そうして描かれるのがQQプロットである。
例えば、ある研究データセットで取得したベースライン時点のWBCの値をQQプロットで正規性を確認してみると以下のような図になる。
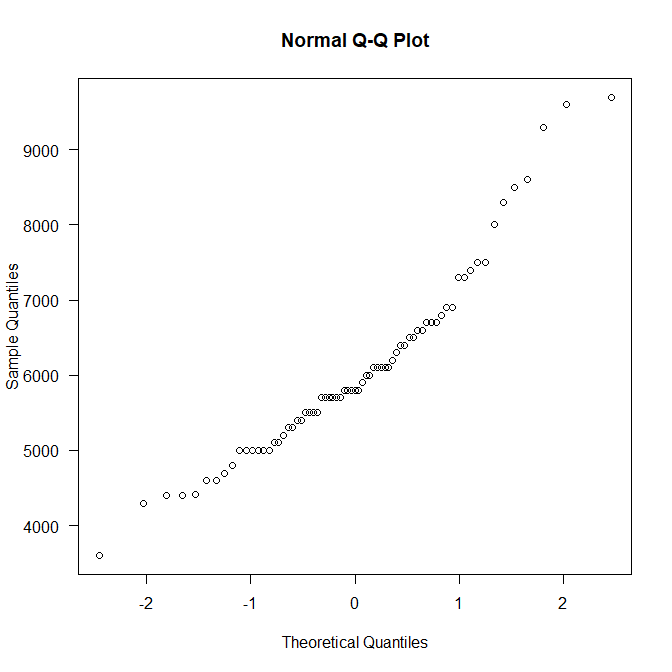
Y軸はWBCの値、X軸はWBCの値のパーセンタイルから計算したクォンタイルである。
Theoretical Quantilesとある。
この理論的なクォンタイルと実際の値の分布が一致すると、対角線上に点が並ぶ。
大体、対角線上に並んでいるようであれば、正規分布していると言ってよい。
このQQプロットは、対角線を引いてみると、その直線状にほぼすべての点が乗っているとはいいがたく、完璧な正規分布とは違うかなという印象があるが、端のほうが従っていないだけで、まるで異なる分布ということでもなさそうである。
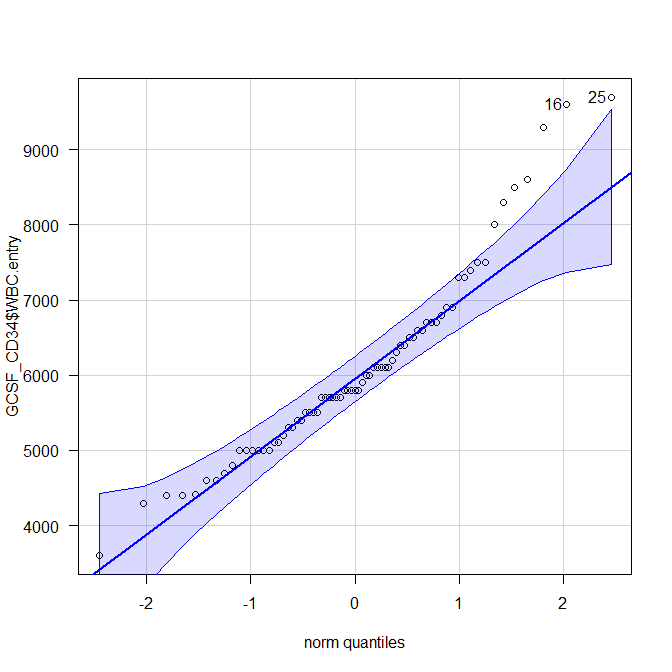
まとめ
連続データの正規性を確認する方法としてQQプロットを紹介した。
QQプロットのX軸とY軸はどういう値なのかを中心に詳しくお伝えした。
何らか参考になれば。
参考サイト
おすすめ書籍
EZR公式マニュアル







コメント