相関係数の比較はどうやるか?
相関係数の差の検定とは?
相関係数の比較 相関係数の差の検定
(この記事で言う相関係数は、すべてPearsonの積率相関係数を指している)
相関係数の差の検定は、以下の検定統計量 T を計算し、標準正規分布で有意確率を求める。
帰無仮説は「2つの母相関係数は等しい」 だ。
$$ T = \frac{\frac{1}{2}\log{\frac{1+r_A}{1-r_A}} – \frac{1}{2}\log{\frac{1+r_B}{1-r_B}}}{\sqrt{\frac{1}{n_A – 3} + \frac{1}{n_B – 3}}} $$
ここで $ r_A $, $ n_A $ は、相関係数Aとそのサンプルサイズ、$ r_B $, $ n_B $ は、相関係数Bとそのサンプルサイズである。
分子は、各群の相関係数をFisherのz変換をしたもの同士の引き算になっている。
Fisherのz変換は、相関係数を正規近似させるための変換である。
この検定統計量が、標準正規分布に従うとして、有意確率を求める。
Rでfunctionを作ってみると以下の通り。
cor.diff.test <- function(nA, rA, nB, rB,
alternative=c("two.sided","one.sided")){
data.name <- sprintf("\nnA=%s, rA=%s\nnB=%s, rB=%s",
nA, rA, nB, rB)
alternative <- match.arg(alternative)
tside <- switch(alternative, one.sided=1, two.sided=2)
zA <- 1/2*log((1+rA)/(1-rA))
zB <- 1/2*log((1+rB)/(1-rB))
ZTRANS <- c(zA, zB)
names(ZTRANS) <- c("Fisher z-transformation: zA",
"Fisher z-transformation: zB")
STATISTICS <- abs((zA-zB)/sqrt(1/(nA-3)+1/(nB-3)))
names(STATISTICS) <- "T"
PVAL <- pnorm(STATISTICS, lower.tail=F)*tside
METHOD <- "Correlation Coefficients Difference Test"
structure (list(statistics=STATISTICS, p.value=PVAL,
estimate=ZTRANS, alternative=alternative,
data.name=data.name, method=METHOD), class="htest")
}
nA=30, rA=-0.459, nB=24, rB=-0.097とした時の検定結果は以下の通りである。
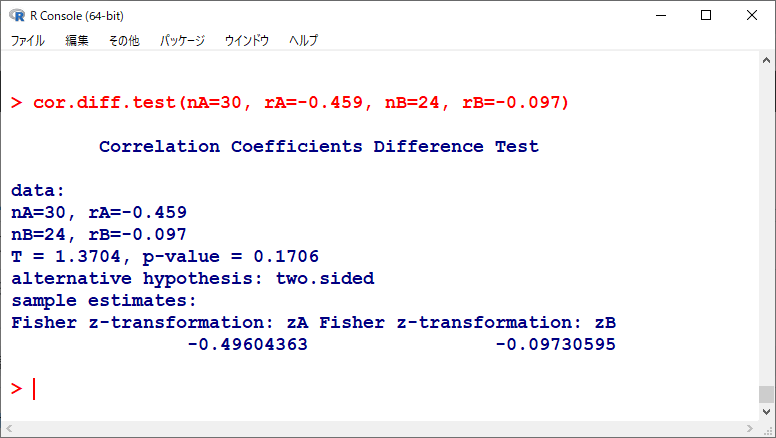
有意水準5%とすると、統計学的有意に差があるとは言えなかった。
相関係数の差の検定をエクセルでできないか?
相関係数の差の検定をエクセルで計算できるようにエクセルファイルを作成した。
よければどうぞ。
相関係数の差の検定【エクセル計算機】 | TKER SHOP
具体的には、こちらの書籍を参考にしている → 医学への統計学 (統計ライブラリー)
相関係数の差の検定をRでもっと簡単にできないか?
統計ソフトRの cocor パッケージを使うと、比較的簡単にできる。
まず、cocor パッケージをインストールする。
統計ソフトRのコンソールに以下を書いてエンター。
install.packages("cocor")
Japanを選んでOKをクリックするとインストールされる。
cocor パッケージを使うときは、library(cocor)で呼び出す。
library(cocor)
相関係数の差の検定をするときは、cocor.indep.groups()関数を使う。
上記の設定と同じ設定で計算してみると以下のようになる。
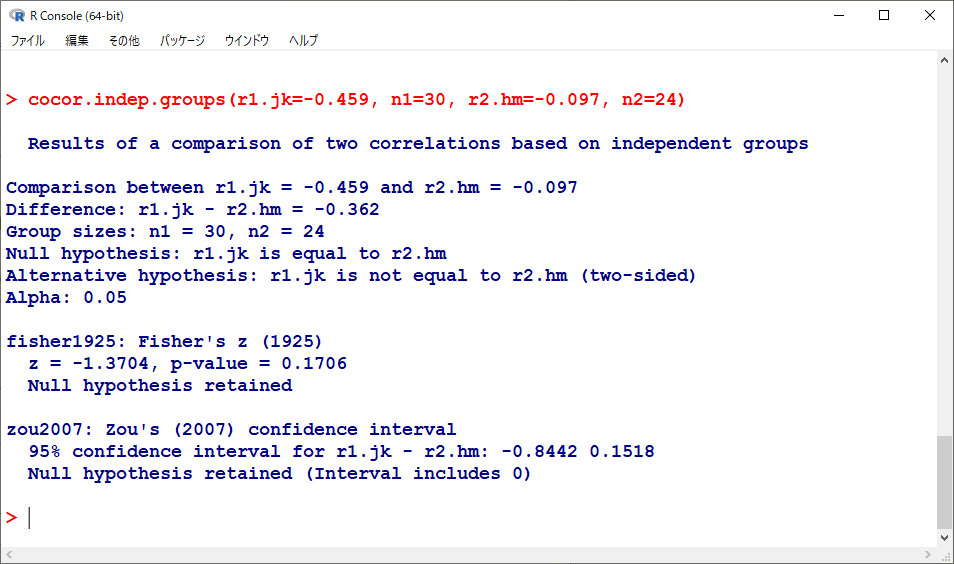
fisher1925とあるところが同じ結果(p-value = 0.1706)になっているのがわかる。
95%信頼区間も計算されている。
このパッケージのマニュアルを見ていたところ、この計算は、完全に独立な相関係数の検定の場合であることがわかった。
psych パッケージの r.test を使う方法
上記と同じことを psych パッケージの r.test を使うと以下のようになる
install.packages("psych") # インストールは最初の一回だけ
library(psych)
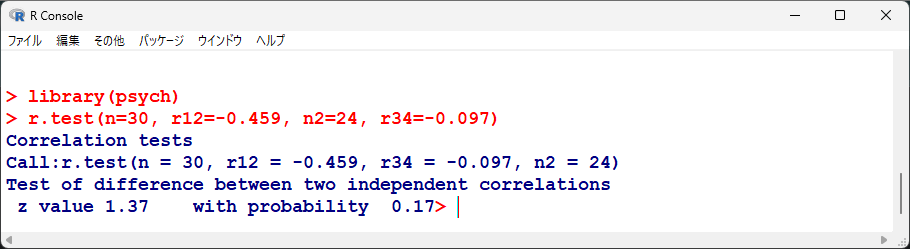
r.test(n=30, r12=-0.459, n2=24, r34=-0.097)結果は以下のとおり、検定統計量 z と P 値が同じであることがわかる
相関係数の差の検定のパッケージ cocor を使いこなす
cocor パッケージは、集計値を使う方法もできれば、生データからの解析もできる優れものだ。
場合分けをして、使い方をまとめてみようと思う。
サンプルデータは、cocor パッケージに含まれている aptitude というデータを用いる。
data("aptitude")
このデータセットは、内部的に二つに分かれており、特殊なデータセットである。
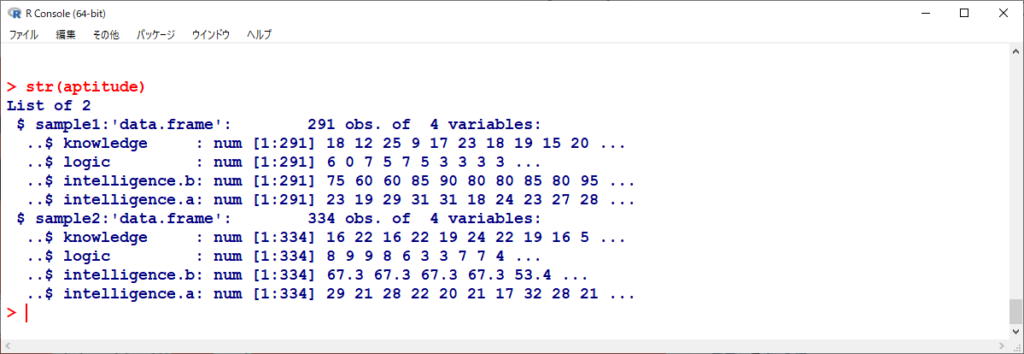
このデータセットの作り方は調べたがわからなかった。
しかし、集計した後に、集計値を使う関数 cocor.indep.groups() に入力すれば計算可能だ(次のセクションに記載あり)。
同じ項目の相関係数を群間比較したい場合
apitudeデータセット内のlogicとintelligence.aの相関係数を、sample1とsample2で比較する形である。
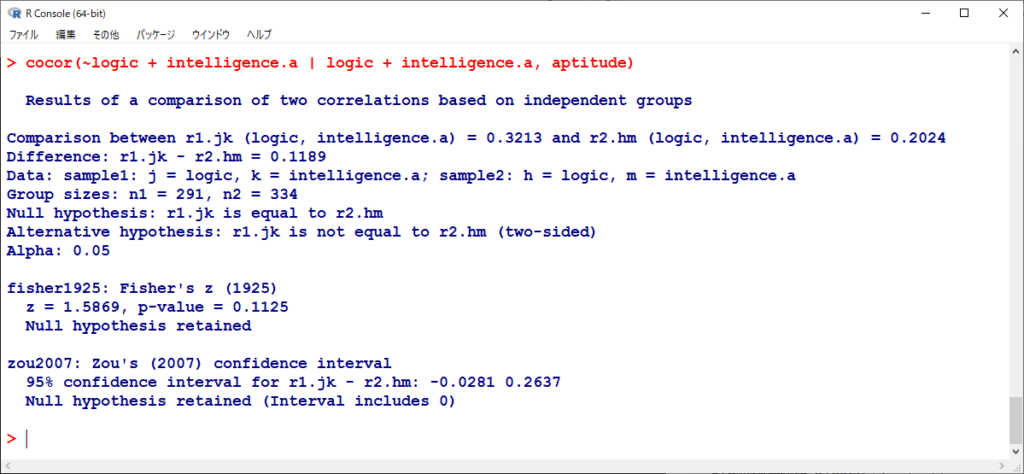
Sample1の相関係数が0.3213, Sample2の相関係数が0.2024である。
それぞれのサンプルサイズは、n1=291, n2=334である。
これは独立2群(Sample1とSample2)であるので、fisher1925の方法で計算されている。
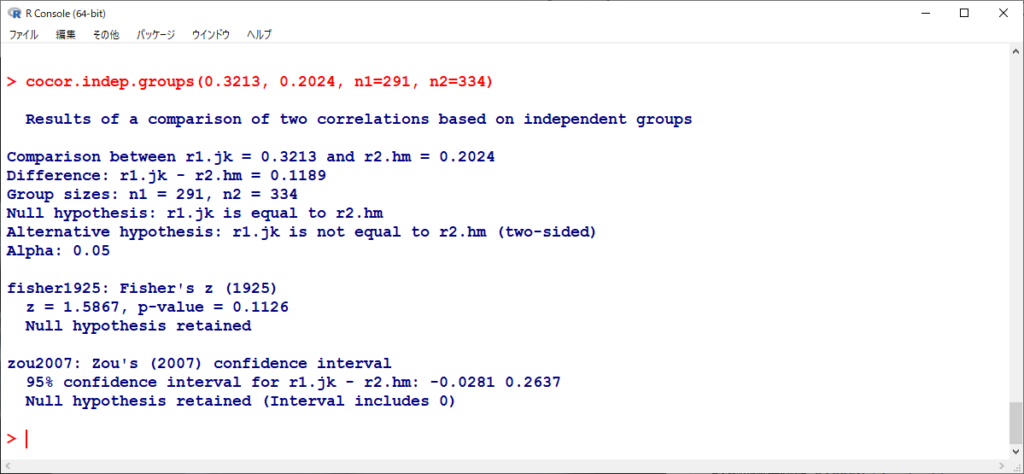
これを cocor.indep.groups()を使ってみると、ほぼ同じ結果になる。
小数点以下4桁より下を端折っているので少しだけ数値は異なる。
同じサンプルの異なる相関係数を比較したい場合(2つの変数のうち1つは同じ)
同じサンプルで、異なる相関係数を比較したいが、完全に独立ではなく、相関係数を計算している2つの変数のうち1つは同じ場合はどうすればよいか?
例として、intelligence.a と knowledge、intelligence.a と logic を比較する。
intelligence.a が重複している。
生データから計算する場合は、cocor()で計算できる。
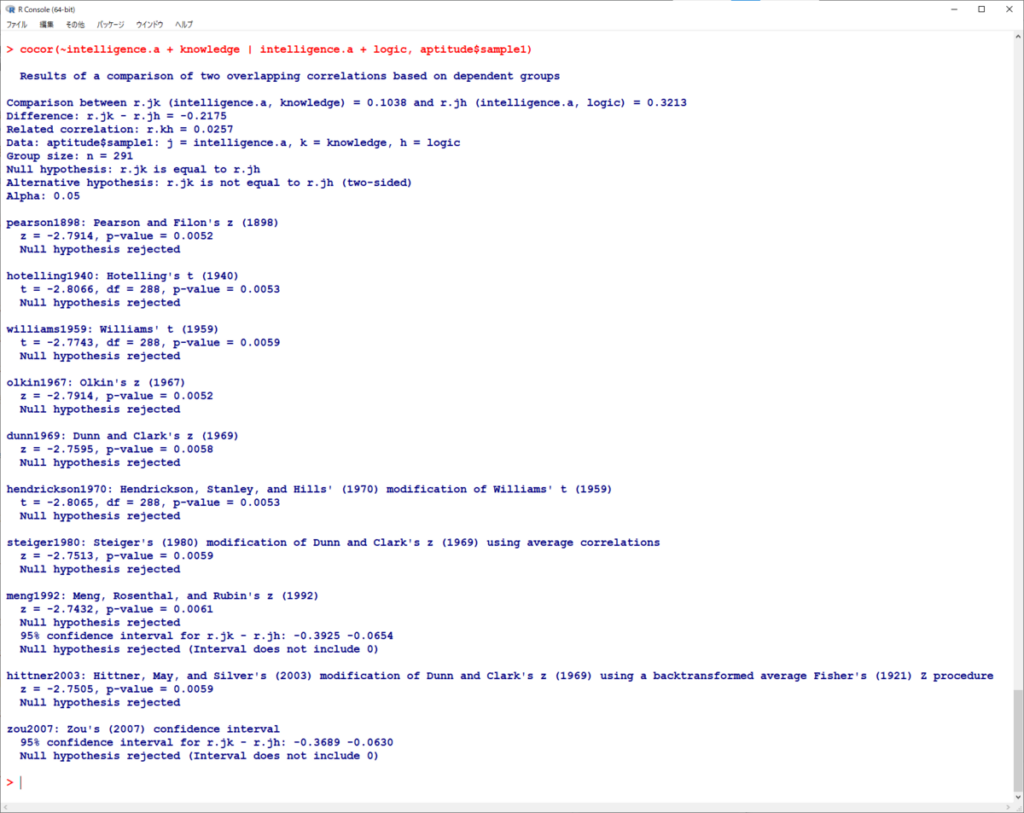
計算すると驚くことに、合計9つの検定結果が出てくる。
これほどまで繰り返し繰り返しよりよい方法が提案されているということに驚きを隠せない。
同時に、どれを採用すればよいかの示唆がないため、初学者には困ってしまう。
これまでの問題点に対処しているはずの最新の方法がもっとも適切なのではないかとは思う。
もっとも、どの方法もほとんど結果は同じである。
これを集計値で計算する場合は、cocor.dep.groups.overlap()関数を使う。
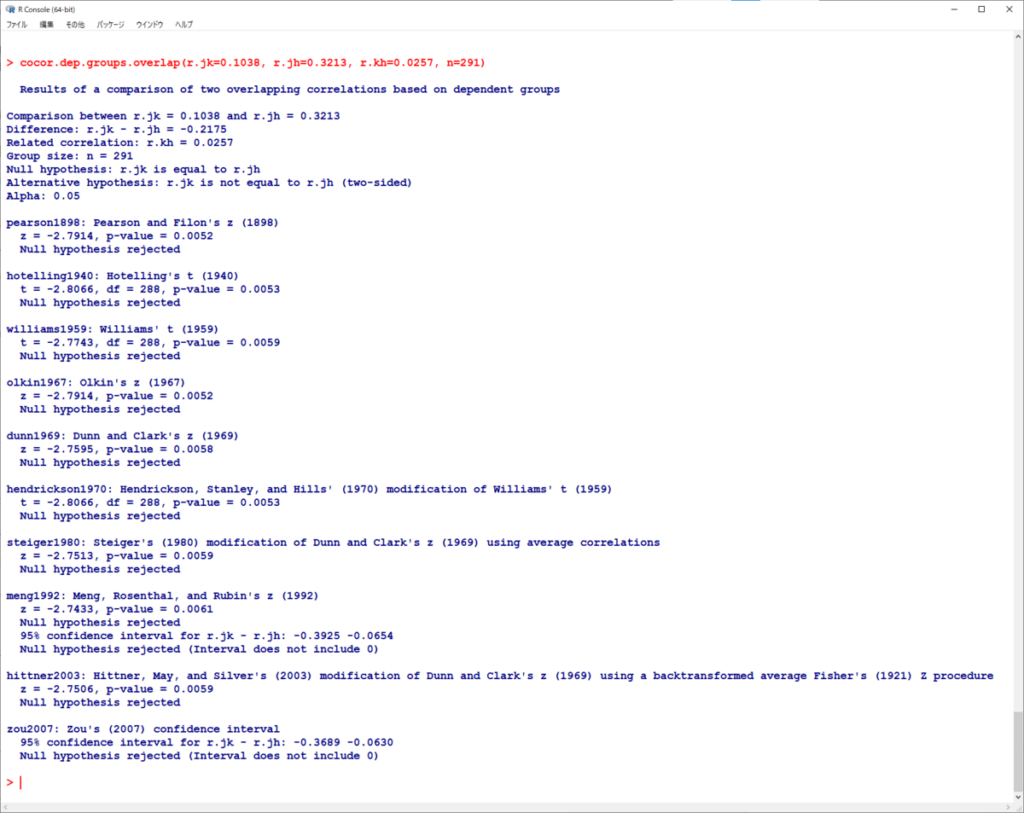
ここでポイントは、重複している変数以外の2つ(ここではknowlegeとlogic)の相関係数(r.kh=0.0257)をインプットする点だ。
これが、完全に独立な場合と異なる点だ。
これを独立の方法で計算するとどうなるか?
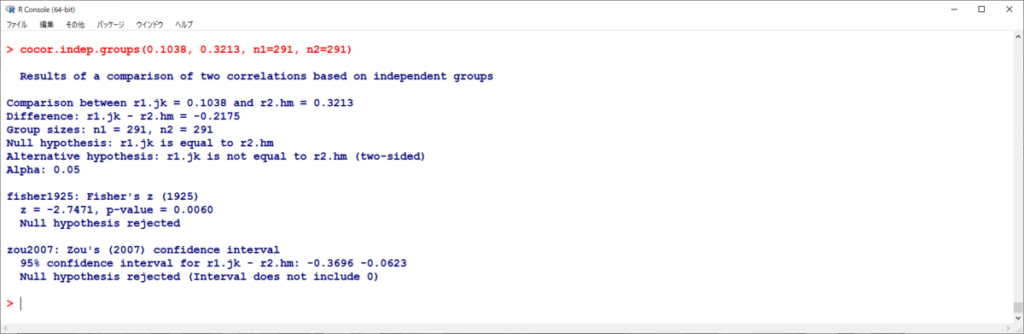
結果はほとんど変わらない。
が、より適切なのは、重複していない変数同士(今回はknowledgeとlogic)の相関を考慮に入れた解析のほうである。
今回はknowledgeとlogicの相関係数が0.0257と、とても小さいため独立の方法と変わりがなかったと考えられる。
重複していない変数同士の相関係数がもっと大きい場合は、違いが出てくるものと思われる。
同じサンプルで異なる相関係数を比較したい場合(それぞれ2つの変数は異なる)
同じサンプルで異なる相関係数を比較したい場合はどうするか?
例えば、logic と intelligence.b、knowledge と intelligence.a の2つの組み合わせとする。
生データからはcocor()を使って計算できる。
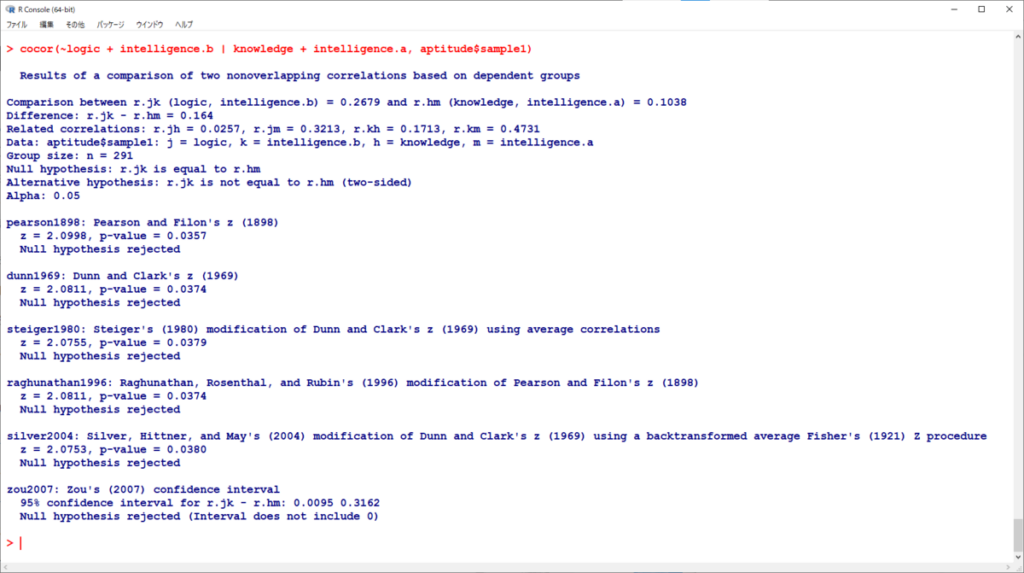
こちらも5つの検定手法の結果が出力される。
どれもほとんど同じ結果であるが、こちらももっとも新しく発表された手法がよいのだろうか。
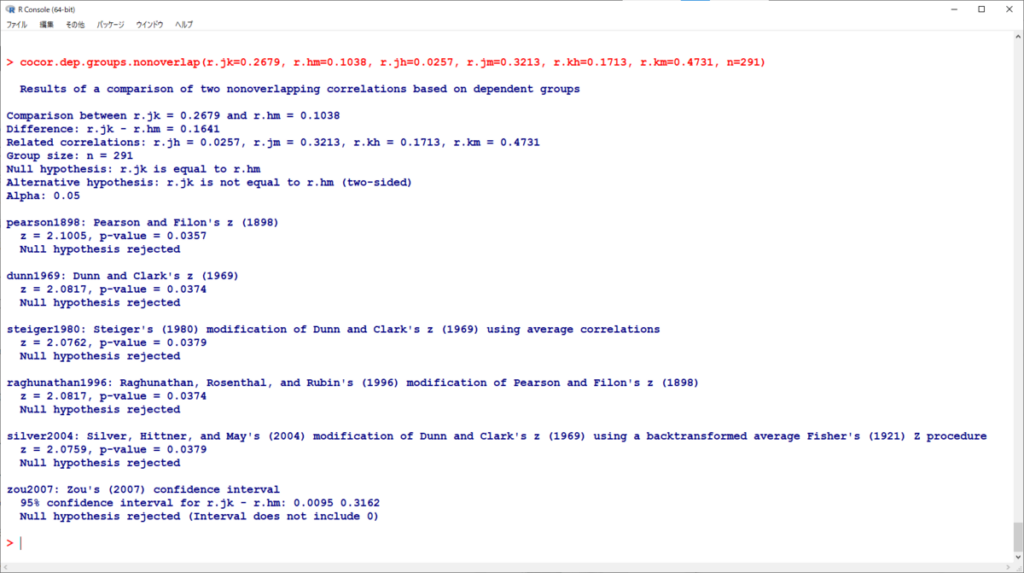
集計値からは、以下のようにして計算できるが、4つの変数のすべての組み合わせ、つまり6つの組み合わせの相関係数を入力する必要がある。
これを独立と考えて計算するとどうなるか?
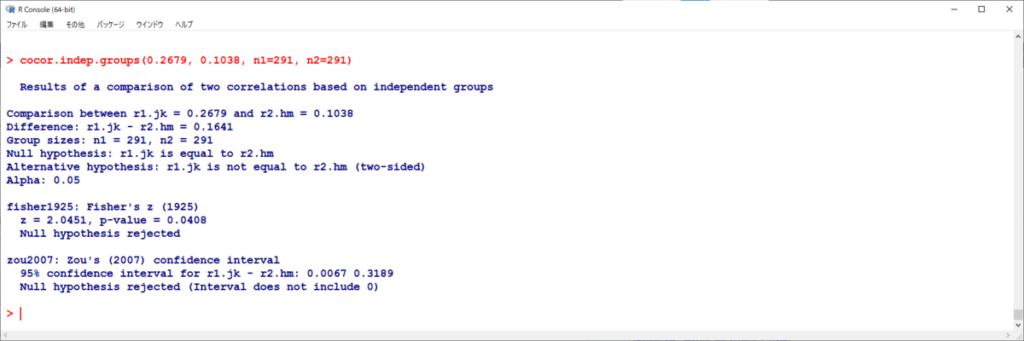
こちらもほぼ同様の結果である。
有意水準を5%とすれば、統計学的有意であることは変わらない。
しかしながら、少し結果が異なるため、できればより適切な方法を使いたい。
まとめ
相関係数の差の検定を紹介した。
Pearsonが発表した1898年から100年以上も経過している解析手法にもかかわらず、EZRやSPSSに実装されていない。
統計ソフトRのパッケージも決して使いやすいとは言えない。
しかも、独立な2つの相関係数の差の検定でない場合は、複数の手法があり、どれを採用すべきなのかわからない。
この状態であると、普及しなくても仕方ないのかもしれない。
Fisherが1925年に発表した独立な2つの相関係数の差の検定で、どのときも大差ない結果が得られるので、どれを使えばよいのか悩むときは、Fisherの方法を採用すればよいのかもしれない。
相関係数の差の検定をエクセルで(Fisher 1925 の方法)
相関係数の差の検定をエクセルで計算できるようにエクセルファイルを作成した。
よければどうぞ。
相関係数の差の検定【エクセル計算機】 | TKER SHOP
具体的には、こちらの書籍を参考にしている → 医学への統計学 (統計ライブラリー)
相関係数の差の検定をアプリで(Fisher 1925 の方法)
デスクトップアプリを作成したので、よければどうぞ
参考PDF(cocorパッケージのマニュアル)
https://cran.r-project.org/web/packages/cocor/cocor.pdf









コメント