差分の差分法(Difference-in-Differences, DiD)は、政策変更や介入の効果を評価する際に非常に強力な統計的手法だ。この記事では、DiDの基本的な考え方から、その使い所、関連する統計手法との違い、DiDの核心である並行トレンドの仮定について詳しく解説し、具体的なRでの計算例、そしてその結果の解釈までを分かりやすく解説する。
差分の差分法の概要
差分の差分法は、ある介入が特定のグループに与える影響を、その介入を受けなかった対照グループと比較することで、因果効果を推定する手法だ。この方法の核心は、「介入グループと対照グループが、介入がなかったとしたら同様のトレンドを辿っていたであろう」という並行トレンドの仮定にある。
DiDは、主に以下の2つの差分を取ることで効果を測定する。
- 時間軸での差分: 介入前と介入後の変化
- グループ間での差分: 介入グループと対照グループ間の変化
これら2つの差分を組み合わせることで、介入による純粋な効果を抽出する。
差分の差分法の使い所
差分の差分法は、以下のような状況で特に有効だ。
- 自然実験: 政策変更や制度導入など、研究者がコントロールできないが、一部のグループにのみ影響を与えるような「自然」に発生した介入の効果を評価する場合。
- 準実験: ランダム化比較試験(RCT)が困難な状況で、介入を受けるグループと受けないグループが存在し、かつ介入前後のデータが利用可能な場合。
- 介入効果の因果的推定: 介入の有無だけでなく、介入後の時間経過による変化を考慮し、他の要因による影響を排除して純粋な介入効果を知りたい場合。
たとえば、新しい法律の導入が犯罪率に与える影響、特定の教育プログラムが学業成績に与える影響、公共交通機関の運賃改定が利用者に与える影響などを分析する際に利用できる。
交互作用項ありの重回帰分析または二元配置分散分析との違い
DiDは、その構造上、交互作用項を含む重回帰分析や二元配置分散分析と非常によく似ている。しかし、その目的と仮定に重要な違いがある。
- 重回帰分析(交互作用項あり): 一般的な重回帰分析に交互作用項を含めることで、ある変数が他の変数の効果をどのように変えるかを評価できる。DiDは、この重回帰モデルの特殊なケースと見なすことができる。DiDにおける交互作用項は、「介入グループであること」と「介入後の期間であること」の組み合わせがアウトカムに与える追加的な影響を表す。
- 二元配置分散分析(Two-way ANOVA): 二元配置分散分析は、2つの要因(例えば、グループと時間)が従属変数に与える影響を評価し、それらの間に交互作用があるかどうかも調べることができる。DiDは、二元配置分散分析の枠組みの中で、「グループ」と「時間」の交互作用効果として介入効果を捉えることができる。
DiDとの本質的な違い:
DiDがこれらの統計手法と異なるのは、単に交互作用効果を検出するだけでなく、その交互作用効果が因果関係を示すと解釈するための強い仮定(並行トレンドの仮定)を必要とすることだ。単なる交互作用項の係数を見るだけでは、「もし介入がなければ、両グループは同じトレンドを辿っていたであろう」という因果的な解釈はできない。DiDは、この並行トレンドの仮定が満たされる場合にのみ、因果効果の推定値として信頼できるものとなる。
並行トレンドの仮定について
並行トレンドの仮定 (Parallel Trends Assumption) は、差分の差分法において最も重要な仮定だ。この仮定は、もし介入が実施されなかったとしたら、介入グループと対照グループのアウトカム(結果変数)は時間とともに同様の傾向をたどっていただろう、ということを意味する。
この仮定が満たされていれば、介入グループと対照グループのアウトカムのトレンドの違いは、介入によるものだと結論づけることができる。しかし、この仮定が破られている場合、DiDによって推定された効果は、介入以外の要因によるものである可能性があり、因果効果を正しく測定できない。
並行トレンドの仮定の検証方法:
- 介入前のトレンドの視覚的確認: 介入前の期間において、介入グループと対照グループのアウトカムの平均値の時系列プロットを作成し、両グループのトレンドが視覚的に並行であるかを確認する。これは、仮定の妥当性を評価するための最も一般的な方法だ。
- 介入前の時点でのダミー変数と介入グループダミーの交互作用項の有意性の確認: 統計的に、介入前の各時点を表すダミー変数と介入グループダミーとの交互作用項を回帰モデルに含め、それらの係数が統計的に有意でないことを確認する。有意な係数がある場合、介入前に既にトレンドに差があったことを示唆する。
- 他の交絡因子の考慮: 介入グループと対照グループで、介入以外の要因が時間とともに異なる影響を与えていないかを検討し、必要であればそれらをモデルに含めて調整する。
並行トレンドの仮定は直接的にテストできるものではなく、過去のデータや関連する理論的根拠に基づいてその妥当性を判断する必要がある。
差分の差分法の具体例
学校給食の無償化が、児童の学習成績に与える影響を評価したいとする。
- 介入グループ: 学校給食が無償化された地域の学校
- 対照グループ: 学校給食が無償化されていない、同様の特性を持つ地域の学校
- 介入前: 給食無償化が実施される前の学習成績
- 介入後: 給食無償化が実施された後の学習成績
この場合、給食無償化によって学習成績がどのように変化したかをDiDで分析する。ここで重要なのは、介入グループと対照グループが、給食無償化がなかったとしても、時間とともに同様のペースで学習成績が変化していたであろう、という並行トレンドの仮定が成り立つことだ。
R 計算例
ここでは、上記の学校給食無償化の例を、Rを使ってDiDを計算する方法を解説する。
R スクリプト例:
# 差分の差分法(Difference-in-Differences, DiD)の例
# 例:給食無償化の効果を評価する(学校単位のデータ)
# サンプルデータの生成(学校単位のデータ)
set.seed(123)
n_treatment_schools <- 30 # 給食無償化を実施した学校数
n_control_schools <- 30 # 給食無償化を実施しなかった学校数
# 各学校の生徒数をランダムに生成
treatment_students <- round(runif(n_treatment_schools, 200, 800))
control_students <- round(runif(n_control_schools, 200, 800))
# 介入グループ(給食無償化実施校)のデータ
# 各学校の介入前後の平均学習成績(100点満点)
treatment_before <- round(rnorm(n_treatment_schools, mean = 65, sd = 8), 1)
treatment_after <- round(treatment_before + rnorm(n_treatment_schools, mean = 8, sd = 4), 1) # 給食効果
# 対照グループ(給食無償化未実施校)のデータ
control_before <- round(rnorm(n_control_schools, mean = 63, sd = 8), 1)
control_after <- round(control_before + rnorm(n_control_schools, mean = 3, sd = 4), 1) # 自然な学習効果
# 学校レベルのデータフレームの作成
school_data <- data.frame(
school_id = 1:(n_treatment_schools + n_control_schools),
group = rep(
c("給食無償化実施校", "給食無償化未実施校"),
c(n_treatment_schools, n_control_schools)
),
students = c(treatment_students, control_students),
score_before = c(treatment_before, control_before),
score_after = c(treatment_after, control_after)
)
# 長い形式(long format)に変換
school_data_long <- data.frame(
school_id = rep(school_data$school_id, 2),
group = rep(school_data$group, 2),
students = rep(school_data$students, 2),
time = rep(c("給食無償化前", "給食無償化後"), each = nrow(school_data)),
score = c(school_data$score_before, school_data$score_after)
)
# timeに順序付けされたレベルを設定
school_data_long$time <- factor(school_data_long$time,
levels = c("給食無償化前", "給食無償化後"),
labels = c("給食無償化前", "給食無償化後"),
ordered = TRUE
)
# ダミー変数の作成
school_data_long$group_dummy <- ifelse(school_data_long$group == "給食無償化実施校", 1, 0)
school_data_long$time_dummy <- ifelse(school_data_long$time == "給食無償化後", 1, 0)
# データの確認
print("=== 学校単位データの概要 ===")
print(head(school_data_long, 10))
print("\n学校別・時点別の平均学習成績:")
school_means <- aggregate(score ~ group + time, data = school_data_long, FUN = mean)
print(school_means)
# 差分の差分法による回帰分析
model <- lm(score ~ group_dummy * time_dummy, data = school_data_long)
# 結果の表示
print("\n=== 差分の差分法による回帰分析結果 ===")
print(summary(model))
# 差分の差分の手動計算
print("\n=== 差分の差分の手動計算 ===")
print(school_means)
# 介入グループの変化
treatment_change <- school_means$score[school_means$group == "給食無償化実施校" & school_means$time == "給食無償化後"] -
school_means$score[school_means$group == "給食無償化実施校" & school_means$time == "給食無償化前"]
# 対照グループの変化
control_change <- school_means$score[school_means$group == "給食無償化未実施校" & school_means$time == "給食無償化後"] -
school_means$score[school_means$group == "給食無償化未実施校" & school_means$time == "給食無償化前"]
# 差分の差分
did_manual <- treatment_change - control_change
cat(sprintf("\n給食無償化実施校の変化: %.2f 点\n", treatment_change))
cat(sprintf("給食無償化未実施校の変化: %.2f 点\n", control_change))
cat(sprintf("差分の差分(手動計算): %.2f 点\n", did_manual))
cat(sprintf("差分の差分(回帰係数): %.2f 点\n", coef(model)["group_dummy:time_dummy"]))
# 可視化
library(ggplot2)
# 平均値のプロット
p1 <- ggplot(school_means, aes(x = time, y = score, group = group, color = group)) +
geom_line(linewidth = 1.5) +
geom_point(size = 3) +
labs(
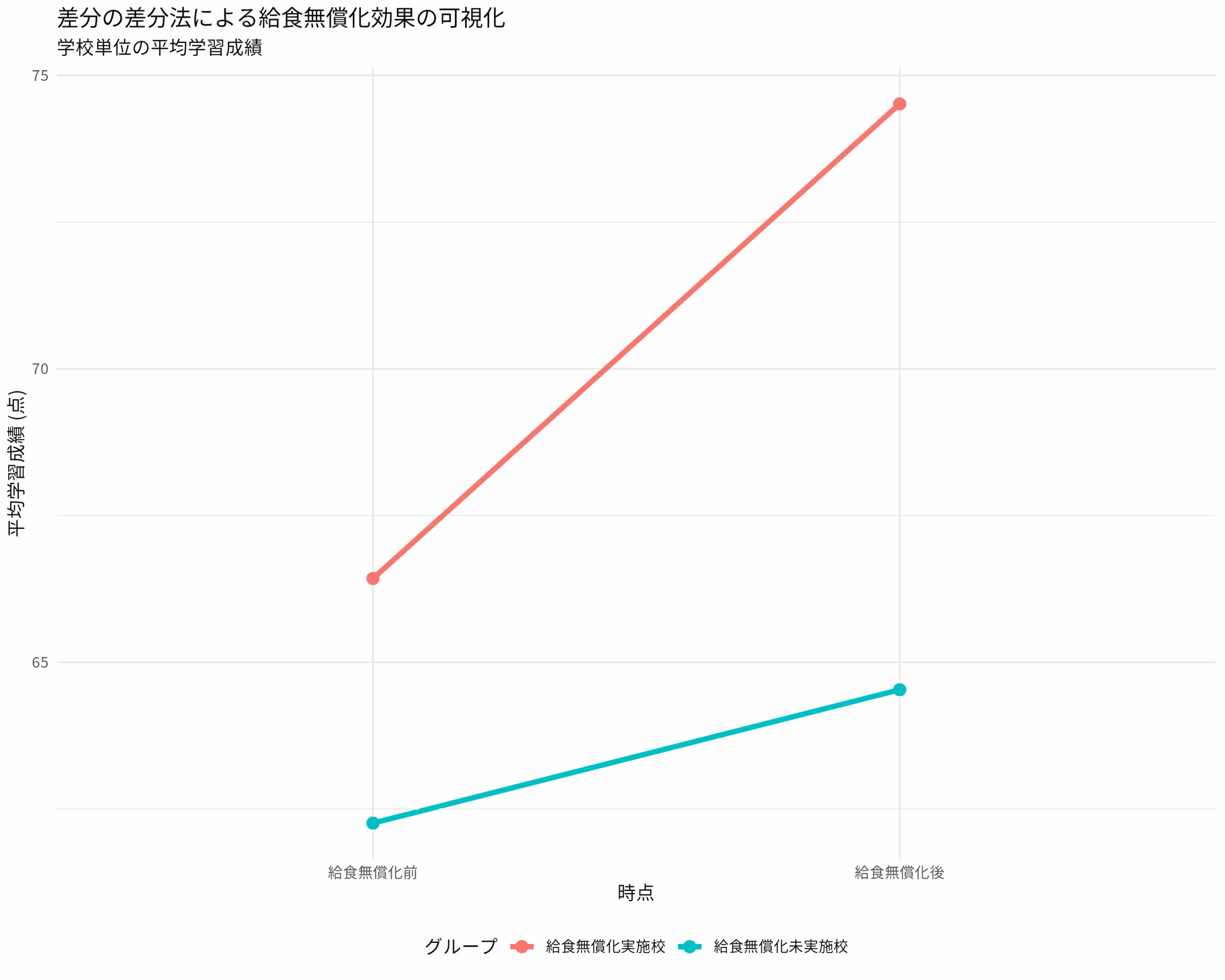
title = "差分の差分法による給食無償化効果の可視化",
subtitle = "学校単位の平均学習成績",
x = "時点", y = "平均学習成績 (点)", color = "グループ"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(p1)
ggsave("Difference-in-difference_method.png", width = 10, height = 8)
実行結果:
> print("\n=== 差分の差分法による回帰分析結果 ===")
[1] "\n=== 差分の差分法による回帰分析結果 ==="
> print(summary(model))
Call:
lm(formula = score ~ group_dummy * time_dummy, data = school_data_long)
Residuals:
Min 1Q Median 3Q Max
-17.730 -4.554 -0.330 4.808 19.870
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 62.257 1.354 45.986 <2e-16 ***
group_dummy 4.170 1.915 2.178 0.0314 *
time_dummy 2.273 1.915 1.187 0.2375
group_dummy:time_dummy 5.817 2.708 2.148 0.0338 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.415 on 116 degrees of freedom
Multiple R-squared: 0.2866, Adjusted R-squared: 0.2681
F-statistic: 15.53 on 3 and 116 DF, p-value: 1.472e-08
>
> print("\n=== 差分の差分の手動計算 ===")
[1] "\n=== 差分の差分の手動計算 ==="
> print(school_means)
group time score
1 給食無償化実施校 給食無償化前 66.42667
2 給食無償化未実施校 給食無償化前 62.25667
3 給食無償化実施校 給食無償化後 74.51667
4 給食無償化未実施校 給食無償化後 64.53000
> cat(sprintf("\n給食無償化実施校の変化: %.2f 点\n", treatment_change))
給食無償化実施校の変化: 8.09 点
> cat(sprintf("給食無償化未実施校の変化: %.2f 点\n", control_change))
給食無償化未実施校の変化: 2.27 点
> cat(sprintf("差分の差分(手動計算): %.2f 点\n", did_manual))
差分の差分(手動計算): 5.82 点
> cat(sprintf("差分の差分(回帰係数): %.2f 点\n", coef(model)["group_dummy:time_dummy"]))
差分の差分(回帰係数): 5.82 点結果解釈
差分の差分法の結果を詳しく解釈する。結論としては、この結果は、給食無償化が児童の学習成績向上に有効であることを示唆している。
係数の意味
切片(Intercept): 62.26点
- 対照グループ(給食無償化未実施校)の介入前の平均学習成績である
- これは基準となる値である
group_dummy: 4.17点
- 介入グループと対照グループの介入前の学習成績差である
- 給食無償化実施校は未実施校より介入前に4.17点高かった
- これは選択バイアスを示しており、実施校の方が元々成績が良かった可能性がある
time_dummy: 2.27点
- 対照グループの介入前後の学習成績変化である
- 給食無償化未実施校でも2.27点の向上があった
- これは時間効果(自然な学習効果、他の要因による向上)を示す
group_dummy:time_dummy: 5.82点 ⭐
- これが差分の差分推定量(給食無償化の純粋な効果)である
- 介入グループの変化(8.09点)から対照グループの変化(2.27点)を引いた値である
- 給食無償化により、学習成績が5.82点向上した
統計的有意性
- group_dummy:time_dummy(5.82点): p = 0.0338 < 0.05
- 5%水準で統計的有意である
- 給食無償化の効果は偶然では説明できない
- group_dummy(4.17点): p = 0.0314 < 0.05
- 介入前の選択バイアスも有意である
- 実施校の方が元々成績が良かった
- time_dummy(2.27点): p = 0.2375 > 0.05
- 時間効果は統計的有意ではない
- 自然な学習効果は明確ではない
差分の差分:手動計算との一致
- 手動計算: 5.82点
- 回帰係数: 5.82点
- 完全に一致しており、計算が正しいことを確認できる
実用的な解釈
- 給食無償化の効果: 学習成績が約6点向上する
- 効果の大きさ: 100点満点で6点の向上は実用的に意味のある効果である
- 政策効果: 給食無償化は学習成績向上に有効な政策介入である
注意点
- 選択バイアス(4.17点)が存在するため、実施校の方が元々成績が良かった可能性がある(最上段の図参照)
- 並行トレンドの仮定が満たされているか確認が必要である(介入前のデータで確認する必要がある)
- 他の要因(教師の質、家庭環境など)の影響を除外できているか検討が必要である
まとめ
差分の差分法は、適切な条件下であれば、政策介入やプログラムの効果を因果的に推定するための強力なツールだ。そのシンプルながらも洗練されたアプローチは、経済学、公衆衛生学、社会学など、様々な分野で活用されている。
しかし、DiDの有効性は並行トレンドの仮定に大きく依存するため、DiDを適用する際にはこの仮定の妥当性を十分に検討することが不可欠だ。この理解が深まれば、より適切な因果推論を行うことができるようになるだろう。




コメント