コレスポンデンス分析(対応分析とも言う) は、大きな分割表に集計されたデータを見やすくする分析方法。
二次元 つまり X軸とY軸に変換して、散布図にして傾向を見る。
コレスポンデンス分析とは?
コレスポンデンス分析とは、対応分析とも呼ばれ、分割表に集計したデータを、行と列それぞれ特徴を分析し、二次元散布図にして傾向を眺めてみる分析方法だ。
三次元も可能だが、二次元が一般的で見やすいと思う。
過去記事はこちら。
コレスポンデンス分析の実際例
サンプルデータ
MASS パッケージの caithデータを使用する。
MASS パッケージを使う準備をする。
MASS は統計ソフトRをインストールした時に、同時にインストールされているので、改めてのインストールは不要。
library(MASS)
caith データは、スコットランドのケイスネス (Caithness)に住む人々の目(光彩)の色と毛髪の色を集計した行列データである。
> caith
fair red medium dark black
blue 326 38 241 110 3
light 688 116 584 188 4
medium 343 84 909 412 26
dark 98 48 403 681 85
実際に分析してみる
分析するための関数はcorresp()である。
行列をcorresp()内に入れる。
nf=で次元の数を指定する。
nf=2と指定すると最終的に二次元プロットになる。
First canonical correlationは、特異値 Singular values とも言われ、固有値 Eigenvaluesの平方根である。
行(row)と列(column)のスコアが計算される。標準座標 Standard coordinatesとも言われる。
corresp1 <- corresp(caith,nf=2)
corresp1
corresp1$cor^2 # eigenvalues
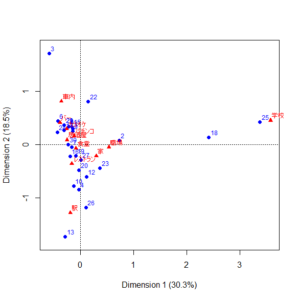
biplot(corresp1) # biplot
corresp1$rscore %*% diag(corresp1$cor)
corresp1$cscore %*% diag(corresp1$cor)
> corresp1 <- corresp(caith, nf=2)
> corresp1
First canonical correlation(s): 0.4463684 0.1734554
Row scores:
[,1] [,2]
blue 0.89679252 0.9536227
light 0.98731818 0.5100045
medium -0.07530627 -1.4124778
dark -1.57434710 0.7720361
Column scores:
[,1] [,2]
fair 1.21871379 1.0022432
red 0.52257500 0.2783364
medium 0.09414671 -1.2009094
dark -1.31888486 0.5992920
black -2.45176017 1.6513565
> corresp1$cor^2 # eigenvalues
[1] 0.19924475 0.03008677
プロットした結果はこちら。
黒字が目の色、赤字が髪の毛の色である。
目の色と髪の色は同じ傾向があり、暗い色と明るい色が一緒になっていると言える。
X軸はプラス値が暗い色、マイナス値が明るい色と言える。
Y軸は、解釈が思い浮かばない。
プロットの値は、以下の計算結果である。
行のスコアと列のスコアそれぞれにCanonical Correlationを掛けている。
スコアの右側から、Canonical Correlationを要素とする対角行列を掛けるとプロット値が計算される。
主成分座標(Principal coordinates)と呼ばれる。
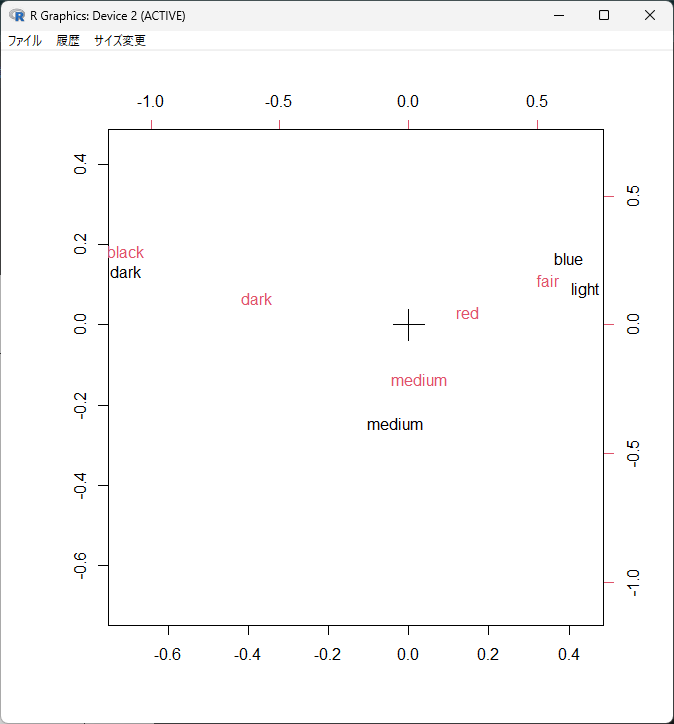
行のプロット(黒)は左と下の目盛り、列のプロット(赤)は右と上の目盛りを使っている。
「二つ」のセット(黒と赤)を一緒にプロットしているのが biplot のゆえんである。
> corresp1$rscore %*% diag(corresp1$cor)
[,1] [,2]
blue 0.40029985 0.16541100
light 0.44070764 0.08846303
medium -0.03361434 -0.24500190
dark -0.70273880 0.13391383
> corresp1$cscore %*% diag(corresp1$cor)
[,1] [,2]
fair 0.54399533 0.17384449
red 0.23326097 0.04827895
medium 0.04202412 -0.20830421
dark -0.58870853 0.10395044
black -1.09438828 0.28643670別のパッケージで分析・プロットしてみる
ca パッケージでも分析・プロットができる。
インストールをしてから利用する。
install.packages("ca")
ca()で分析する。
library(ca)
ca1 <- ca(caith)
plot(ca1)
plot(ca1,mass=TRUE)
ca1$rowcoord %*% diag(ca1$sv)
ca1$colcoord %*% diag(ca1$sv)
固有値と行・列それぞれのスコアが計算される。
スコアは標準座標 Standard coordinatesとも言われる。
$rowcoord, $colcoordで、行と列の標準座標を指定している。
$svは特異値 Singular values(固有値の平方根)だ。
> ca1
Principal inertias (eigenvalues):
1 2 3
Value 0.199245 0.030087 0.000859
Percentage 86.56% 13.07% 0.37%
Rows:
blue light medium dark
Mass 0.133284 0.293299 0.329311 0.244106
ChiDist 0.437855 0.450620 0.247359 0.715398
Inertia 0.025553 0.059557 0.020149 0.124932
Dim. 1 0.896793 0.987318 -0.075306 -1.574347
Dim. 2 0.953623 0.510004 -1.412478 0.772036
Columns:
fair red medium dark black
Mass 0.270095 0.053091 0.396696 0.258214 0.021905
ChiDist 0.571235 0.265854 0.212526 0.597901 1.132193
Inertia 0.088134 0.003752 0.017918 0.092308 0.028079
Dim. 1 1.218714 0.522575 0.094147 -1.318885 -2.451760
Dim. 2 1.002243 0.278336 -1.200909 0.599292 1.651357プロットの結果はこちら。
corresp()のbiplot()と違って、行も列も同じ目盛りを使っている。
青字が目の色で、赤字が髪の毛の色だ。
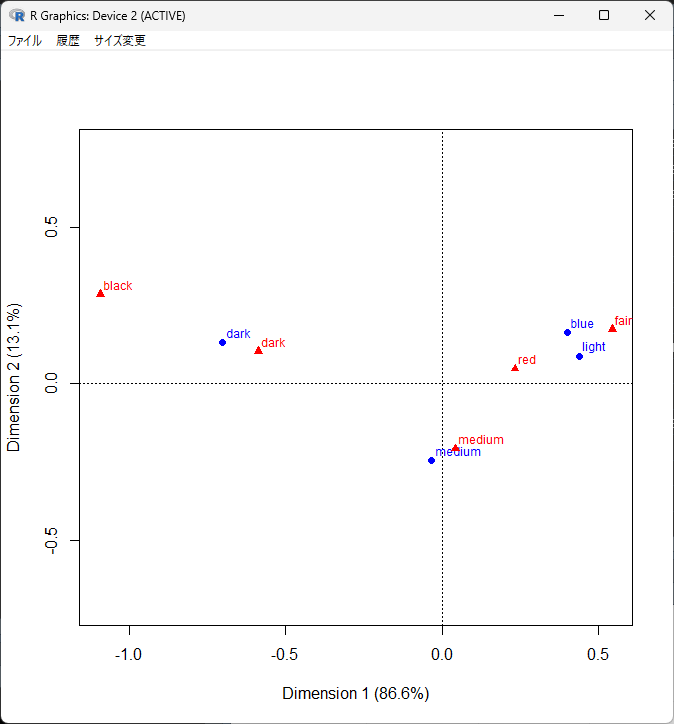
Dimension1(X軸)は、目の色と髪の色が、プラス値で暗い色、マイナス値で明るい色であることはわかる。
Dimension2(Y軸)の意味合いは明らかでない。
X軸とY軸のラベルに86.6%と13.1%と書いてある。
これは固有値全体における割合を示している。
Dimension1は86.6%で固有値の大半を占めていて、Dimension1だけで大半説明がつくという意味になる。
ゆえにDimension2にうまい解釈がつかないのも納得できる。
mass=TRUEを追加すると、nの大きさによってポイントの大きさが変わる。
nが多いとポイントが大きくなる。
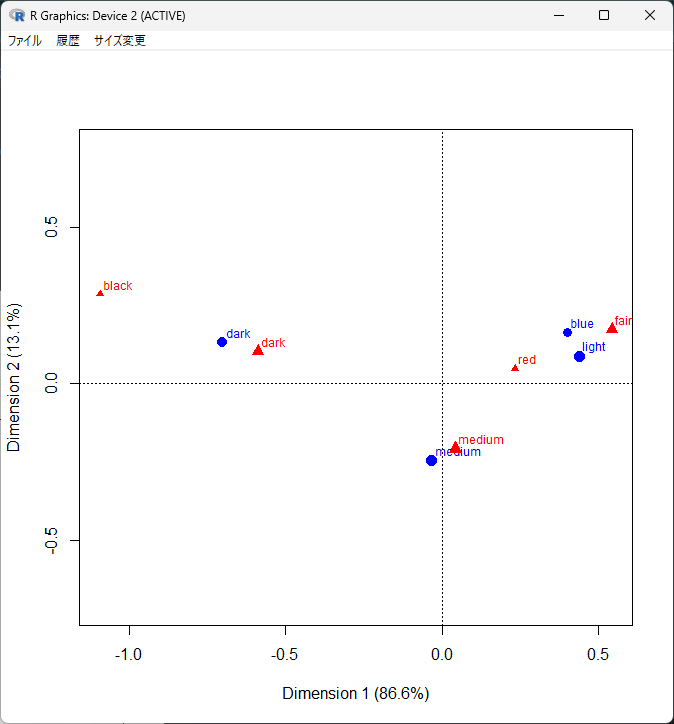
プロットの座標は、標準座標に特異値(Singular values)を掛けた主成分座標(Principal coordinates)を用いている。
プロットには一列目をDimension1(X軸)、二列目をDimension2(Y軸)に用いている。
> ca1$rowcoord %*% diag(ca1$sv)
[,1] [,2] [,3]
blue 0.40029985 0.16541100 -0.064157519
light 0.44070764 0.08846303 0.031773257
medium -0.03361434 -0.24500190 -0.005552885
dark -0.70273880 0.13391383 0.004345377
> ca1$colcoord %*% diag(ca1$sv)
[,1] [,2] [,3]
fair 0.54399533 0.17384449 -0.012522082
red 0.23326097 0.04827895 0.118054940
medium 0.04202412 -0.20830421 -0.003236468
dark -0.58870853 0.10395044 -0.010116315
black -1.09438828 0.28643670 0.046135954コレスポンデンス分析をstep by stepで実施してみる
標準残差 Standard Residuals を計算することがコレスポンデンス分析のキモとなる。
標準残差は、二乗して合計すると独立性の検定に使うカイ二乗 $ \chi^2 $ 値になる。
標準残差は、観察値と期待値の「隔たり」を表現したものになる。
n <- sum(caith)
f.row <- rowSums(caith)
f.col <- colSums(caith)
f.mat <- caith
z.ij <- matrix(rep(0,20),nr=4)
for (i in 1:4){
for (j in 1:5){
z.ij[i,j] <- (f.mat[i,j]/n-f.row[i]*f.col[j]/n^2)/(sqrt(f.row[i]*f.col[j])/n)
}
}
z.ij # Standard Residuals 標準残差
Q.t <- z.ij %*% t(z.ij)
Q <- t(z.ij) %*% z.ij
eigen.row <- eigen(Q.t) # 行の特徴を固有値・固有ベクトルに凝縮する
eigen.col <- eigen(Q) # 列の特徴を固有値・固有ベクトルに凝縮する
# 行と列の周辺割合の平方根の逆数で固有ベクトルを規準化したものがスコア(標準座標)になる
D.r <- diag(1/sqrt(f.row/n))
D.c <- diag(1/sqrt(f.col/n))
# 標準座標 Standard coordinates
D.r %*% eigen.row$vectors
D.c %*% eigen.col$vectors
# 主成分座標 Pricipal coordinates
D.r %*% eigen.row$vectors %*% diag(sqrt(eigen.row$values))
D.c %*% eigen.col$vectors %*% diag(sqrt(eigen.col$values))
標準残差は以下のように計算される。
> z.ij # Standard Residuals 標準残差
[,1] [,2] [,3] [,4] [,5]
[1,] 0.1292162 -0.0002629922 -0.03538203 -0.07544543 -0.04372599
[2,] 0.1723046 0.0477768696 -0.02328106 -0.14838434 -0.07088969
[3,] -0.0847428 -0.0142960921 0.10542144 -0.02932898 -0.02810479
[4,] -0.1859232 -0.0355710546 -0.07078163 0.25246345 0.14265843
標準残差の行方向の二乗にあたるQ.tと列方向の二乗に当たるQは以下の通り。
> Q.t <- z.ij %*% t(z.ij)
> Q <- t(z.ij) %*% z.ij
> Q.t
[,1] [,2] [,3] [,4]
[1,] 0.02555277 0.03737037 -0.011234763 -0.046795636
[2,] 0.03737037 0.05955678 -0.011394621 -0.079661660
[3,] -0.01123476 -0.01139462 0.020149468 -0.002611605
[4,] -0.04679564 -0.07966166 -0.002611605 0.124931987
> Q
[,1] [,2] [,3] [,4] [,5]
[1,] 0.088134492 1.602317e-02 -4.357128e-03 -0.07976947 -0.042006558
[2,] 0.016023167 3.752377e-03 -9.232812e-05 -0.01563060 -0.008048110
[3,] -0.004357128 -9.232812e-05 1.791761e-02 -0.01483772 -0.009862943
[4,] -0.079769470 -1.563060e-02 -1.483772e-02 0.09230791 0.050658169
[5,] -0.042006558 -8.048110e-03 -9.862943e-03 0.05065817 0.028078616
Q.tとQそれぞれから固有値・固有ベクトルを求めると以下の通り。固有値($values)が行、列ともに3つまでは同じ値であることがわかる。
> eigen.row <- eigen(Q.t) # 行の特徴を固有値・固有ベクトルに凝縮する
> eigen.col <- eigen(Q) # 列の特徴を固有値・固有ベクトルに凝縮する
> eigen.row
eigen() decomposition
$values
[1] 1.992448e-01 3.008677e-02 8.594814e-04 -9.238255e-18
$vectors
[,1] [,2] [,3] [,4]
[1,] -0.32740153 0.3481491 0.79894718 0.3650806
[2,] -0.53470247 0.2762034 -0.58694655 0.5415706
[3,] 0.04321499 -0.8105596 0.10869354 0.5738565
[4,] 0.77783929 0.3814407 -0.07323162 0.4940710
> eigen.col
eigen() decomposition
$values
[1] 1.992448e-01 3.008677e-02 8.594814e-04 7.761727e-18 -5.800482e-18
$vectors
[,1] [,2] [,3] [,4] [,5]
[1,] -0.63337328 0.5208721 0.22198126 -0.5274987 0.00000000
[2,] -0.12040878 0.0641327 -0.92784507 -0.1825513 -0.29524104
[3,] -0.05929716 -0.7563782 0.06953154 -0.6464176 0.04105527
[4,] 0.67018848 0.3045289 0.17534533 -0.4302105 -0.49222197
[5,] 0.36286535 0.2444040 -0.23291035 -0.2923755 0.81784150
行と列の周辺割合(f.row/n, f.col/n)の平方根の逆数で固有ベクトルを規準化したものがスコアになる。
「割合の平方根の逆数」ベクトルの対角行列(D.r, D.c)をそれぞれ左から掛ける。
D.r, D.cは以下の通り。
> # 行と列の周辺割合の平方根の逆数で固有ベクトルを規準化したものがスコア(標準座標)になる
> D.r <- diag(1/sqrt(f.row/n))
> D.c <- diag(1/sqrt(f.col/n))
> D.r
[,1] [,2] [,3] [,4]
[1,] 2.739121 0.000000 0.000000 0.000
[2,] 0.000000 1.846481 0.000000 0.000
[3,] 0.000000 0.000000 1.742596 0.000
[4,] 0.000000 0.000000 0.000000 2.024
> D.c
[,1] [,2] [,3] [,4] [,5]
[1,] 1.924164 0.000000 0.00000 0.000000 0.000000
[2,] 0.000000 4.340007 0.00000 0.000000 0.000000
[3,] 0.000000 0.000000 1.58771 0.000000 0.000000
[4,] 0.000000 0.000000 0.00000 1.967931 0.000000
[5,] 0.000000 0.000000 0.00000 0.000000 6.756667
固有ベクトルと掛け算するとスコアになる。
標準座標 Standard coordinates とも言われる。
> # 標準座標 Standard coordinates
> D.r %*% eigen.row$vectors
[,1] [,2] [,3] [,4]
[1,] -0.89679252 0.9536227 2.1884132 1
[2,] -0.98731818 0.5100045 -1.0837859 1
[3,] 0.07530627 -1.4124778 0.1894089 1
[4,] 1.57434710 0.7720361 -0.1482208 1
> D.c %*% eigen.col$vectors
[,1] [,2] [,3] [,4] [,5]
[1,] -1.21871379 1.0022432 0.4271282 -1.0149937 0.00000000
[2,] -0.52257500 0.2783364 -4.0268545 -0.7922741 -1.28134829
[3,] -0.09414671 -1.2009094 0.1103959 -1.0263237 0.06518388
[4,] 1.31888486 0.5992920 0.3450676 -0.8466247 -0.96865900
[5,] 2.45176017 1.6513565 -1.5736976 -1.9754840 5.52588230
上記の結果の二列目までが、corresp()やca()の結果と一致する。
第一成分は、符号が逆であるが、同じものと考えてよい。
> corresp1
First canonical correlation(s): 0.4463684 0.1734554
Row scores:
[,1] [,2]
blue 0.89679252 0.9536227
light 0.98731818 0.5100045
medium -0.07530627 -1.4124778
dark -1.57434710 0.7720361
Column scores:
[,1] [,2]
fair 1.21871379 1.0022432
red 0.52257500 0.2783364
medium 0.09414671 -1.2009094
dark -1.31888486 0.5992920
black -2.45176017 1.6513565Dim.1, Dim.2 の行を見ると、上記の最初の 2 列と同じ値であることがわかる。
> ca1
Principal inertias (eigenvalues):
1 2 3
Value 0.199245 0.030087 0.000859
Percentage 86.56% 13.07% 0.37%
Rows:
blue light medium dark
Mass 0.133284 0.293299 0.329311 0.244106
ChiDist 0.437855 0.450620 0.247359 0.715398
Inertia 0.025553 0.059557 0.020149 0.124932
Dim. 1 0.896793 0.987318 -0.075306 -1.574347
Dim. 2 0.953623 0.510004 -1.412478 0.772036
Columns:
fair red medium dark black
Mass 0.270095 0.053091 0.396696 0.258214 0.021905
ChiDist 0.571235 0.265854 0.212526 0.597901 1.132193
Inertia 0.088134 0.003752 0.017918 0.092308 0.028079
Dim. 1 1.218714 0.522575 0.094147 -1.318885 -2.451760
Dim. 2 1.002243 0.278336 -1.200909 0.599292 1.651357標準座標 Standard coordinatesに、右側から固有値の平方根(特異値 Singular values)を要素とする対角行列を掛けると、主成分座標 Principal coordinatesになる。
これがcorresp()やca()のプロット座標になっている。
左から一列目をDimension1(X軸)に、二列目をDimension2(Y軸)にしている。
> # 主成分座標 Pricipal coordinates
> D.r %*% eigen.row$vectors %*% diag(sqrt(eigen.row$values))
[,1] [,2] [,3] [,4]
[1,] -0.40029985 0.16541100 0.064157519 NaN
[2,] -0.44070764 0.08846303 -0.031773257 NaN
[3,] 0.03361434 -0.24500190 0.005552885 NaN
[4,] 0.70273880 0.13391383 -0.004345377 NaN
警告メッセージ:
sqrt(eigen.row$values) で: 計算結果が NaN になりました
> D.c %*% eigen.col$vectors %*% diag(sqrt(eigen.col$values))
[,1] [,2] [,3] [,4] [,5]
[1,] -0.54399533 0.17384449 0.012522082 -2.827760e-09 NaN
[2,] -0.23326097 0.04827895 -0.118054940 -2.207266e-09 NaN
[3,] -0.04202412 -0.20830421 0.003236468 -2.859325e-09 NaN
[4,] 0.58870853 0.10395044 0.010116315 -2.358686e-09 NaN
[5,] 1.09438828 0.28643670 -0.046135954 -5.503674e-09 NaN
警告メッセージ:
sqrt(eigen.col$values) で: 計算結果が NaN になりました
固有値・固有ベクトルとは?
固有値・固有ベクトルとは、データから作ったデータの特徴を表す行列を、変換して計算した値・ベクトルと言える。
たとえば、データから作った特徴の行列を A とする。
下記を満たす λ が固有値、x が固有ベクトルと言われる。
$$ \boldsymbol{Ax} = \lambda \boldsymbol{x} $$
固有値、固有ベクトルはいくつも存在する。
上記Q.tに関しては、eigen()で求めると4つ計算される。
特徴の行列(今回はQ.t)の行(または列)と同じ数だけ計算される。
データから作った行列を、ギュッと凝縮したものが、固有値・固有ベクトルだと言える。
> Q.t
[,1] [,2] [,3] [,4]
[1,] 0.02555277 0.03737037 -0.011234763 -0.046795636
[2,] 0.03737037 0.05955678 -0.011394621 -0.079661660
[3,] -0.01123476 -0.01139462 0.020149468 -0.002611605
[4,] -0.04679564 -0.07966166 -0.002611605 0.124931987
> eigen.row <- eigen(Q.t) # 行の特徴を固有値・固有ベクトルに凝縮する
> eigen.row
eigen() decomposition
$values
[1] 1.992448e-01 3.008677e-02 8.594814e-04 -9.238255e-18
$vectors
[,1] [,2] [,3] [,4]
[1,] -0.32740153 0.3481491 0.79894718 0.3650806
[2,] -0.53470247 0.2762034 -0.58694655 0.5415706
[3,] 0.04321499 -0.8105596 0.10869354 0.5738565
[4,] 0.77783929 0.3814407 -0.07323162 0.4940710
検算してみると $ \boldsymbol{Ax} = \lambda \boldsymbol{x} $ であることが確認できる。
## 左辺
> Q.t %*% eigen.row$vector[,1]
[,1]
[1,] -0.06523304
[2,] -0.10653666
[3,] 0.00861036
[4,] 0.15498040
## 右辺
> matrix(eigen.row$value[1]*eigen.row$vector[,1])
[,1]
[1,] -0.06523304
[2,] -0.10653666
[3,] 0.00861036
[4,] 0.15498040
Singular Value DecompositionでStep by step
さきほどはeigen()を使って、固有値・固有ベクトルを求めたが、svd()を使う方法もある。
SVD は、Singular Value Decomposition の頭文字語で、特異値(Singular values)と固有ベクトルに分解する方法だ。
特異値は、固有値の平方根だ。
canonical correlationとも呼ばれる。
標準残差行列を以下のように分解できる。
$$ \boldsymbol{z_{ij}} = \boldsymbol{U D_{\alpha} V^T } $$
ここで $ D_{\alpha} $ は、特異値を要素とする対角行列、U、V はそれぞれ、行と列の固有ベクトルである。
S.svd <- svd(z.ij) # Singular Value Decompsition
S.svd$d # Singular values
S.svd$d^2 # Eigenvalues or principal inertia
S.svd$u # Eigenvector of row
S.svd$v # Eigenvector of column
S.svd$u %*% diag(S.svd$d) %*% t(S.svd$v) # 標準残差行列
z.ij # for confirmation
D.r %*% S.svd$u # 標準座標 Standard coordinates
D.c %*% S.svd$v # 標準座標 Standard coordinates
D.r %*% S.svd$u %*% diag(S.svd$d) # 主成分座標 Principal coordinates
D.c %*% S.svd$v %*% diag(S.svd$d) # 主成分座標 Principal coordinates特異値 Singular values の二乗が固有値になる。
> S.svd$d # Singular values
[1] 4.463684e-01 1.734554e-01 2.931691e-02 1.829859e-17
> S.svd$d^2 # Eigenvalues
[1] 1.992448e-01 3.008677e-02 8.594814e-04 3.348386e-34
行の固有ベクトルと列の固有ベクトルは以下の通り。
> S.svd$u # Eigenvector of row
[,1] [,2] [,3] [,4]
[1,] 0.32740153 0.3481491 -0.79894718 0.3650806
[2,] 0.53470247 0.2762034 0.58694655 0.5415706
[3,] -0.04321499 -0.8105596 -0.10869354 0.5738565
[4,] -0.77783929 0.3814407 0.07323162 0.4940710
> S.svd$v # Eigenvector of column
[,1] [,2] [,3] [,4]
[1,] 0.63337328 0.5208721 -0.22198126 -0.06089658
[2,] 0.12040878 0.0641327 0.92784507 -0.31434151
[3,] 0.05929716 -0.7563782 -0.06953154 -0.03384428
[4,] -0.67018848 0.3045289 -0.17534533 -0.53859621
[5,] -0.36286535 0.2444040 0.23291035 0.77862039
特異値を成分とした対角行列の左右から、行の固有ベクトル U と列の固有ベクトル V (の転置行列)を掛けると、もとの標準残差行列になる。
以下の式の通りだ。
$$ \boldsymbol{z_{ij}} = \boldsymbol{U D_{\alpha} V^T} $$
> S.svd$u %*% diag(S.svd$d) %*% t(S.svd$v) # 標準残差行列
[,1] [,2] [,3] [,4] [,5]
[1,] 0.1292162 -0.0002629922 -0.03538203 -0.07544543 -0.04372599
[2,] 0.1723046 0.0477768696 -0.02328106 -0.14838434 -0.07088969
[3,] -0.0847428 -0.0142960921 0.10542144 -0.02932898 -0.02810479
[4,] -0.1859232 -0.0355710546 -0.07078163 0.25246345 0.14265843
> z.ij # for confirmation
[,1] [,2] [,3] [,4] [,5]
[1,] 0.1292162 -0.0002629922 -0.03538203 -0.07544543 -0.04372599
[2,] 0.1723046 0.0477768696 -0.02328106 -0.14838434 -0.07088969
[3,] -0.0847428 -0.0142960921 0.10542144 -0.02932898 -0.02810479
[4,] -0.1859232 -0.0355710546 -0.07078163 0.25246345 0.14265843
固有ベクトルに左側から「割合の平方根の逆数」ベクトルの対角行列(D.r, D.c)をそれぞれ左から掛けると、スコアになるのは上述と同様。
corresp()やca()が返すスコアだ。
標準座標 Standard coordinatesとも言う。
> D.r %*% S.svd$u # 標準座標 Standard coordinates
[,1] [,2] [,3] [,4]
[1,] 0.89679252 0.9536227 -2.1884132 1
[2,] 0.98731818 0.5100045 1.0837859 1
[3,] -0.07530627 -1.4124778 -0.1894089 1
[4,] -1.57434710 0.7720361 0.1482208 1
> D.c %*% S.svd$v # 標準座標 Standard coordinates
[,1] [,2] [,3] [,4]
[1,] 1.21871379 1.0022432 -0.4271282 -0.11717498
[2,] 0.52257500 0.2783364 4.0268545 -1.36424450
[3,] 0.09414671 -1.2009094 -0.1103959 -0.05373491
[4,] -1.31888486 0.5992920 -0.3450676 -1.05992031
[5,] -2.45176017 1.6513565 1.5736976 5.26087829
さらに右側から特異値を要素とする対角行列を掛けると、主成分座標 Principal coordinates になる。
これがcorresp()やca()のプロット座標になっている。
左から一列目をDimension1(X軸)に、二列目をDimension2(Y軸)にしている。
> D.r %*% S.svd$u %*% diag(S.svd$d) # 主成分座標 Principal coordinates
[,1] [,2] [,3] [,4]
[1,] 0.40029985 0.16541100 -0.064157519 1.829859e-17
[2,] 0.44070764 0.08846303 0.031773257 1.829859e-17
[3,] -0.03361434 -0.24500190 -0.005552885 1.829859e-17
[4,] -0.70273880 0.13391383 0.004345377 1.829859e-17
> D.c %*% S.svd$v %*% diag(S.svd$d) # 主成分座標 Principal coordinates
[,1] [,2] [,3] [,4]
[1,] 0.54399533 0.17384449 -0.012522082 -2.144138e-18
[2,] 0.23326097 0.04827895 0.118054940 -2.496376e-17
[3,] 0.04202412 -0.20830421 -0.003236468 -9.832734e-19
[4,] -0.58870853 0.10395044 -0.010116315 -1.939505e-17
[5,] -1.09438828 0.28643670 0.046135954 9.626668e-17まとめ
コレスポンデンス分析をcorresp()とca()を使って実施してみた。
さらにeigen()やsvd()を使って、step by stepで実施してみた。
分割表にまとめられた結果が、行の要素と列の要素それぞれ、どのような関係にあるかを図によって眺めることができる興味深い方法だ。
大きな分割表で、行と列の対応が把握しきれない場合、有効な分析方法と言える。
参考になれば。
参考文献
対応分析によるデータ解析
https://www.kwansei.ac.jp/s_sociology/attached/6779_56340_ref.pdf









コメント