R で生存時間データを分析する方法

Coxの比例ハザードモデル（コックスの比例ハザードモデル、Cox回帰、コックス回帰など表示・呼び名はたくさんあるが皆同じものを指している）は、生存時間とイベントデータを多変量解析できる統計モデルだ。

注目したい要因が、他の要因と相関があり、また他の要因がイベントにも影響を与えている（交絡要因と呼ばれる）ときに用いられる方法だ。

R で Cox 回帰の方法の解説。

RでCox比例ハザードモデルを実施するためのサンプルデータ

survival パッケージの lung データセットを使う。

これは、北部中央がん治療グループ（North Central Cancer Treatment Group, NCCTG）提供の進行肺がん患者さんの生存データ。

詳しくはこちらも参照。

まず、survivalを呼び出す。

library(survival)

全身状態を表すECOG performance scoreで見ると、データセット中でもっとも状態が悪い３の症例が一例しかいない。

今回は計算や作図のわかりやすさの関係上、その一例を除外して進める。

現実のデータ解析では、こういう一例を除外するかどうか、除外するなら適切な理由がつくかどうか、大変慎重に進める必要があるのは言うまでもない。

lung1 <- lung[lung$ph.ecog<3,]

RでCox比例ハザードモデルを実施する準備

カプランマイヤー曲線とログランク検定でエンドポイントとの関連を確認しておく

今回、ECOG performance scoreで生存時間に違いがあるかの解析を行う。

性別や年齢は生存・死亡に関連あるのは言うまでもないが、ECOG performance scoreにも関連あると仮定する。

まず、ECOG performance score別に生存期間が異なるか検討する。

survfit1 <- survfit(Surv(time,status)~factor(ph.ecog),data=lung1)
plot(survfit1, col=2:4, las=1, xlab="Survival Time (days)", ylab="Overall Survival")
legend("topright", paste("ECOG PS=",0:2, sep=""), lty=1, col=2:4)
survfit1
survdiff(Surv(time,status)~factor(ph.ecog),data=lung1)

ECOG performance score順にだんだん予後が悪くなるのがわかる。

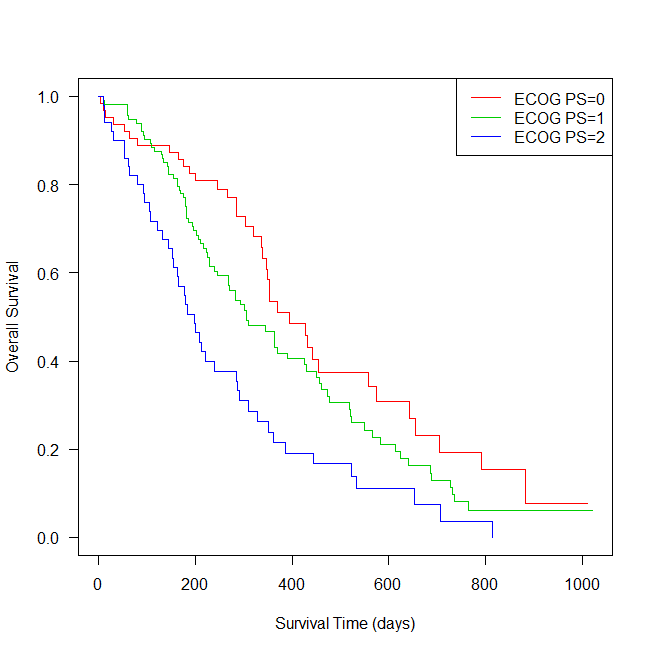
survfit()の結果は、ECOG performance score別に、n、イベント数、生存日数中央値、95%信頼区間下限、上限が表示される。

survdiff()の結果は、ログランク検定の結果で、ECOG performance score間で統計学的に有意な差があることがわかる（ p=1e-04 = $ 10^4 $ = 0.001 ）。

> survfit1
Call: survfit(formula = Surv(time, status) ~ factor(ph.ecog), data = lung1)
1 observation deleted due to missingness
n events median 0.95LCL 0.95UCL
factor(ph.ecog)=0  63     37    394     348     574
factor(ph.ecog)=1 113     82    306     268     429
factor(ph.ecog)=2  50     44    199     156     288
> survdiff(Surv(time,status)~factor(ph.ecog),data=lung1)
Call:
survdiff(formula = Surv(time, status) ~ factor(ph.ecog), data = lung1)
n=226, 1 observation deleted due to missingness.
N Observed Expected (O-E)^2/E (O-E)^2/V
factor(ph.ecog)=0  63       37     53.9    5.3014    8.0181
factor(ph.ecog)=1 113       82     83.1    0.0144    0.0295
factor(ph.ecog)=2  50       44     26.0   12.4571   14.9754
Chisq= 18  on 2 degrees of freedom, p= 1e-04

次に、性別で生存期間が異なるか確認する。

survfit2 <- survfit(Surv(time,status)~factor(sex),data=lung1)
plot(survfit2,col=1:2, las=1, xlab="Survival Time (days)", ylab="Overall Survival")
legend("topright", c("Male","Female"), lty=1, col=1:2)
survfit2
survdiff(Surv(time,status)~factor(sex),data=lung1)

グラフを見ると女性のほうが生存期間が長く見える。

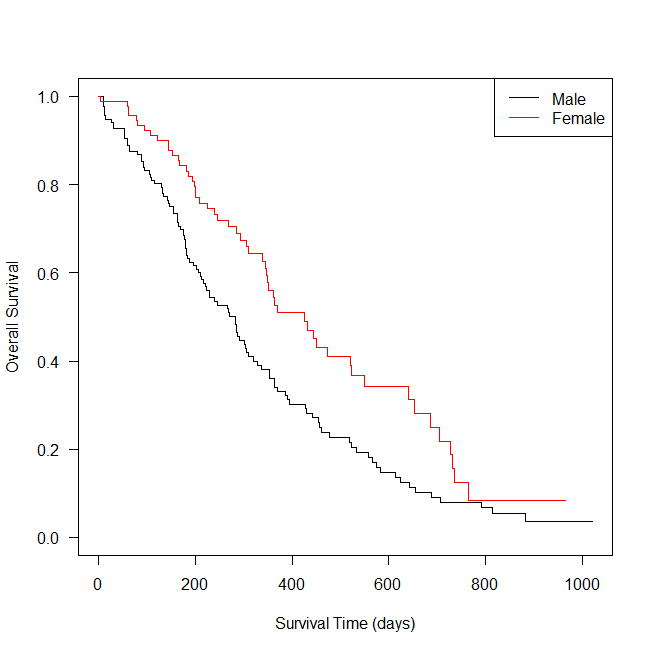
結果は、女性（sex=2）のほうが男性（sex=1）に比べ、生存期間中央値が長く、ログランク検定でも統計学的に有意な差があった（ p = 0.002 ）。

> survfit2
Call: survfit(formula = Surv(time, status) ~ factor(sex), data = lung1)
1 observation deleted due to missingness
n events median 0.95LCL 0.95UCL
factor(sex)=1 136    110    283     218     320
factor(sex)=2  90     53    426     348     550
> survdiff(Surv(time,status)~factor(sex),data=lung1)
Call:
survdiff(formula = Surv(time, status) ~ factor(sex), data = lung1)
n=226, 1 observation deleted due to missingness.
N Observed Expected (O-E)^2/E (O-E)^2/V
factor(sex)=1 136      110     90.3      4.29      9.72
factor(sex)=2  90       53     72.7      5.33      9.72
Chisq= 9.7  on 1 degrees of freedom, p= 0.002

それでは年齢はどうか？

10歳の区切りを中心に、約10年間隔でグループを作って、予備的に検討してみる。

lung1$agec <- round(lung1$age/10)
table(lung1$age, lung1$agec) # 加工した変数の確認

グラフを描いて、ログランク検定をしてみる。

survfit3 <- survfit(Surv(time,status)~agec, data=lung1)
plot(survfit3,col=1:5, las=1, xlab="Survival Time (days)", ylab="Overall Survival")
legend("topright", paste("Around", (4:8)*10), lty=1, col=1:5)
survfit3
survdiff(Surv(time,status)~agec,data=lung1)

グラフからは、年齢グループで大きな差は見られない。

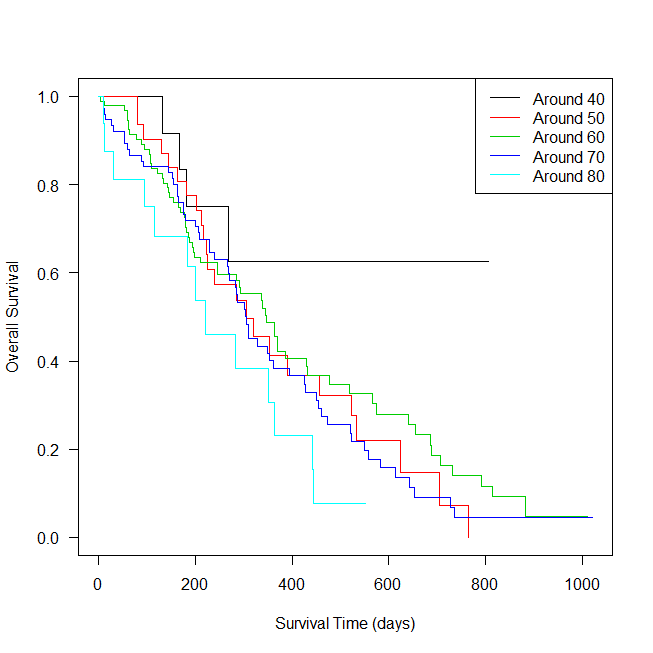
生存日数中央値を見ても、ログランク検定の結果を見ても、顕著な差は見られず、死亡と強い関連はないと言える。

> survfit3
Call: survfit(formula = Surv(time, status) ~ agec, data = lung1)
1 observation deleted due to missingness
n events median 0.95LCL 0.95UCL
agec=4 12      4     NA     268      NA
agec=5 31     24    305     223     533
agec=6 92     63    348     285     477
agec=7 75     59    306     269     426
agec=8 16     13    222     116      NA
> survdiff(Surv(time,status)~agec,data=lung1)
Call:
survdiff(formula = Surv(time, status) ~ agec, data = lung1)
n=226, 1 observation deleted due to missingness.
N Observed Expected (O-E)^2/E (O-E)^2/V
agec=4 12        4     9.33    3.0490    3.2724
agec=5 31       24    23.13    0.0328    0.0386
agec=6 92       63    68.84    0.4956    0.8695
agec=7 75       59    53.91    0.4816    0.7249
agec=8 16       13     7.79    3.4844    3.7060
Chisq= 7.7  on 4 degrees of freedom, p= 0.1

とはいうものの、生死にかかわる一番の要因は年齢なので、年齢は共変量から外さずに進むことにする。

多変量モデルの変数は、最終的には研究者が決めるもの。

途中の計算は参考として考え、最終モデルは研究者が決める。

興味のある変数と共変量の関連をみておく

今回興味がある変数はECOG performance scoreである。

このスコアが性別や年齢で異なるかどうか見ておく必要がある。

ほぼ相関がなければ、いくらエンドポイントに関係している予後因子でも、調整しなくてよい。

交絡因子の条件を満たさないためだ。

交絡因子の条件は以下の 3 つ

1. 予後因子である
2. 相関がある
3. 中間因子ではない

逆に少しでも関連性を感じれば、調整しておくほうが無難だ。

まず、ECOG performance scoreと性別の関連を見る。

ECOG performance scoreは3段階、性別は男女で2つなので、3×2の分割表で考える。

ECOGには順番があるが、そのトレンドがどうというよりも、3グループで性別の割合が違うかだけを見ることにする。

この場合Fisher Exact Testを使う。

with(lung1, fisher.test(ph.ecog, sex))

結果は、p = 0.7059 で統計学的有意ではない。

関連あるとは言えない。

> with(lung1, fisher.test(ph.ecog, sex))
Fisher's Exact Test for Count Data
data:  ph.ecog and sex
p-value = 0.7059
alternative hypothesis: two.sided

次に、年齢との関連も見ておく。

年齢は連続量と考えて、一元配置分散分析で検討することにする。

lm()とanova()を使う。

分散分析について詳しくはこちらを参照。

lm1 <- lm(age ~ factor(ph.ecog), data=lung1)
anova(lm1)

結果は、ECOG performance score間で年齢の分布は統計学的有意に異なることがわかった。

これは、多変量モデルで調整するのが望ましい。

ただし、今回のデータは年齢がエンドポイントにあまり関連していないので、それほど大きな意味合いはないかもしれない。

> anova(lm1)
Analysis of Variance Table
Response: age
Df  Sum Sq Mean Sq F value   Pr(>F)
factor(ph.ecog)   2   928.2  464.12  5.8484 0.003345 **
Residuals       223 17697.0   79.36
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’

ECOG performance score別の生存時間を検討するのに、性別と年齢は必ずしも大きな影響を持っていないかもしれないという結果であるが、今回はこのまま多変量調整をする方向で進んでみる。

R で coxph を使って Cox比例ハザードモデルを実際に適用してみる

R でCoxの比例ハザードモデルを実施するには survival パッケージの coxph() という関数を使う。

coxph() のカッコ内はsurvfit()やsurvdiff()によく似ている。

また、~（チルダ）よりも右側は、lm()やglm()と書き方がそっくりだ。

ECOG performance scoreだけで適用してみる

coxph1 <- coxph(Surv(time,status)~factor(ph.ecog),data=lung1)
summary(coxph1)

summary() で結果を見てみると、ECOG performance scoreが２の場合が、０に比べて、統計学的有意にハザード比（Hazard ratio）が高いことがわかる。

exp(coef)の欄を見る。

推定値と95%信頼区間は、2.498 (1.6083-3.878)である。

０に比べて、２の症例は2.5倍イベントが起きやすかったと言える。

> summary(coxph1)
Call:
coxph(formula = Surv(time, status) ~ factor(ph.ecog), data = lung1)
n= 226, number of events= 163
(1 observation deleted due to missingness)
coef exp(coef) se(coef)     z Pr(>|z|)
factor(ph.ecog)1 0.3686    1.4458   0.1987 1.856   0.0635 .
factor(ph.ecog)2 0.9153    2.4975   0.2246 4.076 4.58e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
factor(ph.ecog)1     1.446     0.6917    0.9795     2.134
factor(ph.ecog)2     2.498     0.4004    1.6083     3.878
Concordance= 0.602  (se = 0.024 )
Likelihood ratio test= 16.53  on 2 df,   p=3e-04
Wald test            = 17.28  on 2 df,   p=2e-04
Score (logrank) test = 18.04  on 2 df,   p=1e-04

ECOG performance scoreに加えて性別と年齢を投入してみる

coxph2 <- coxph(Surv(time,status)~factor(ph.ecog)+factor(sex)+age,data=lung1)
summary(coxph2)

結果として、ECOG performance scoreは先ほどと同じく０に比べて、２の症例は約2.5倍のハザードであると計算された。

ECOG performance scoreが１であっても、０に比べて、有意にリスクが高かった（約1.5倍）。

また、男性に比べ、女性のほうが約0.58倍のハザードであり、約42%ほどリスクが低いことがわかる。

> summary(coxph2)
Call:
coxph(formula = Surv(time, status) ~ factor(ph.ecog) + factor(sex) +
age, data = lung1)
n= 226, number of events= 163
(1 observation deleted due to missingness)
coef exp(coef)  se(coef)      z Pr(>|z|)
factor(ph.ecog)1  0.409836  1.506571  0.199606  2.053  0.04005 *
factor(ph.ecog)2  0.902321  2.465318  0.228092  3.956 7.62e-05 ***
factor(sex)2     -0.545631  0.579476  0.168229 -3.243  0.00118 **
age               0.010777  1.010836  0.009312  1.157  0.24713
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
factor(ph.ecog)1    1.5066     0.6638    1.0188    2.2279
factor(ph.ecog)2    2.4653     0.4056    1.5766    3.8550
factor(sex)2        0.5795     1.7257    0.4167    0.8058
age                 1.0108     0.9893    0.9926    1.0295
Concordance= 0.635  (se = 0.025 )
Likelihood ratio test= 28.94  on 4 df,   p=8e-06
Wald test            = 28.6  on 4 df,   p=9e-06
Score (logrank) test = 29.68  on 4 df,   p=6e-06

統計学的な規準による変数選択を参考までに見てみる

MASS パッケージの stepAIC() という関数は、AIC (Akaike’s Information Criterion) の観点から、最適なモデルを選んでくれる関数。

AICとは？

赤池情報量規準 – Wikipedia

library(MASS)
stepAIC(coxph2)

年齢は統計学的有意でないことがこちらでも反映され、年齢を除いたECOG performance scoreと性別だけのモデルが最適モデルとして選ばれた。

最下段を参照。

> stepAIC(coxph2)
Start:  AIC=1457.19
Surv(time, status) ~ factor(ph.ecog) + factor(sex) + age
Df    AIC
- age              1 1456.5
<none>               1457.2
- factor(sex)      1 1466.3
- factor(ph.ecog)  2 1468.8
Step:  AIC=1456.55
Surv(time, status) ~ factor(ph.ecog) + factor(sex)
Df    AIC
<none>               1456.5
- factor(sex)      1 1465.6
- factor(ph.ecog)  2 1470.1
Call:
coxph(formula = Surv(time, status) ~ factor(ph.ecog) + factor(sex),
data = lung1)
coef exp(coef) se(coef)      z        p
factor(ph.ecog)1  0.4180    1.5189   0.1995  2.096   0.0361
factor(ph.ecog)2  0.9464    2.5765   0.2248  4.211 2.54e-05
factor(sex)2     -0.5447    0.5800   0.1681 -3.240   0.0012
Likelihood ratio test=27.58  on 3 df, p=4.451e-06
n= 226, number of events= 163
(1 observation deleted due to missingness)

この統計学的な規準による変数選択の結果も踏まえて、最終モデルは研究者が決める。

まとめ

Coxの比例ハザードモデルを R で実行してみた。

解析の準備段階として、survfit() でカプランマイヤー曲線を描いたり、survdiff() でログランク検定を行う必要がある。

また、交絡要因の検討として、カテゴリならFisher Exact Test、連続量で三群以上なら一元配置分散分析（二群なら平均値の差の検定）で検討する。

最終的には coxph() 関数を使って多変量解析をする。

stepAIC() で最終的な変数選択の参考とする結果を得ることができる。