R で時系列データを分析するための基礎的な方法の解説。
時系列データとは何か?
時系列データとは、日時のデータと値のデータのペアのこと。
例としては、
- 四半期ごとの売上高。
- 毎月の経費。
- 週当たりの納入量。
- 毎日の株価・ドル円レート。
など。
こういう定期的に得られたデータを時系列データと呼ぶ。
時系列データ分析を実施する理由は?
時系列データ分析の目的の一つは未来予測にある。
時間によって値がどのように変化しているか、その規則をとらえて、今後どのように推移するかを予測したい。
未来予測が大きな目的の一つだ。
時系列データの例
時系列データの例として、ドル円レートを挙げる。
みずほ銀行のヒストリカルデータをダウンロードして一行目と二行目を削除する。
csvファイルを読み込む。
Windowsのドキュメントフォルダ内の data というフォルダに入れたとすると以下のスクリプトで読み込める。
dat<-read.csv("data/tm_quote.csv",header=TRUE)
日付とドル円レートのデータだけを取り出して、時系列データにする。
d1 <- (dat[,2])
時系列分析の例
時系列解析を R で実施するために、まずは時系列データであることを知らせる必要がある。
時系列データであることを知らせる関数は ts() である。
ts.d1 <- ts(d1)
時系列データの図示
どんなデータもまずは図示してみると全体がつかめる。
plot(ts.d1,xlab="Working Day from 06-Jan-2020",ylab="USD-JPY rate",las=1)
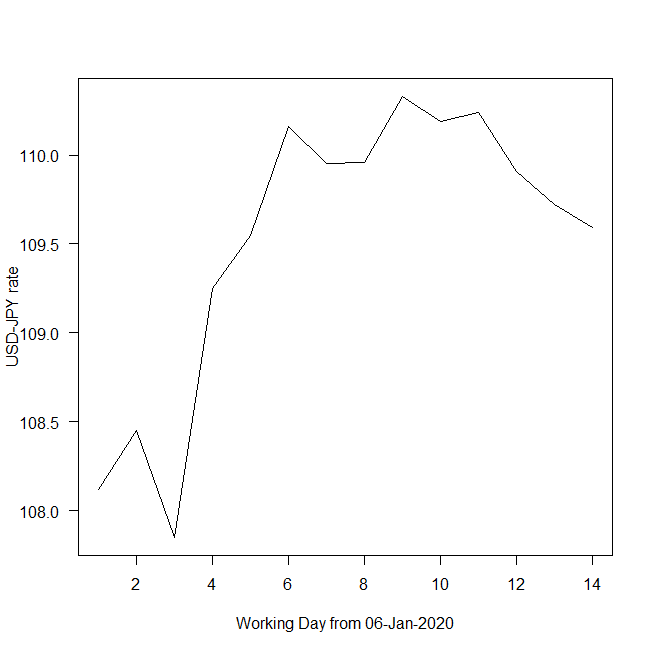
時系列データの差分を求める
時系列データ分析の目的の一つはパターンを見出すことだ。
一つ前との差分、二つ前との差分、三つ前との差分・・・など、いくつか前との差分を取ることで、パターンが見えてきたりする。
差分を取るときの関数が diff() で、どのくらい前の差分を取るかが lag= という変数だ。
例えば一営業日前とすると、
plot(diff(ts.d1,lag=1))
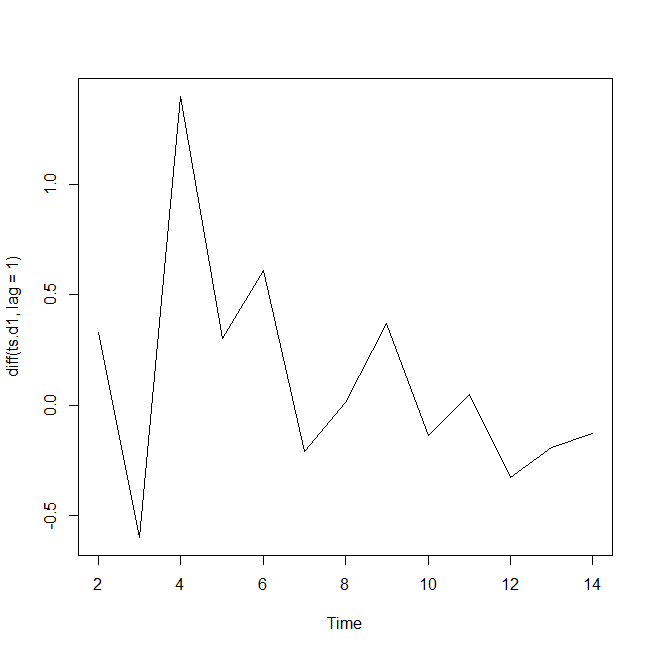
二営業日とすると、
plot(diff(ts.d1,lag=2))
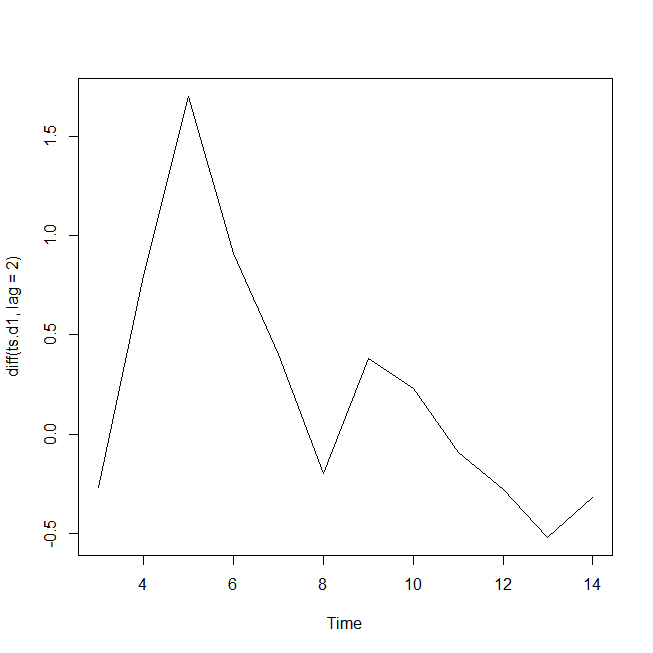
三営業日とすると、
plot(diff(ts.d1,lag=3))
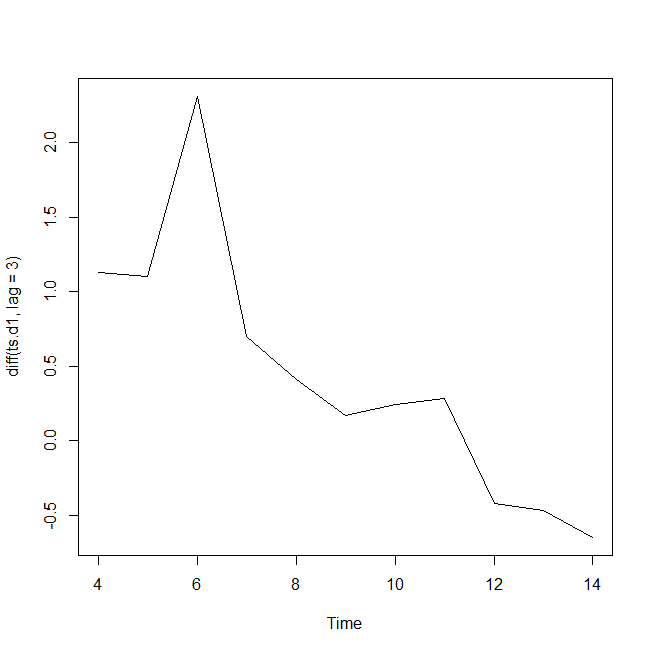
四営業日とすると、
plot(diff(ts.d1,lag=4))
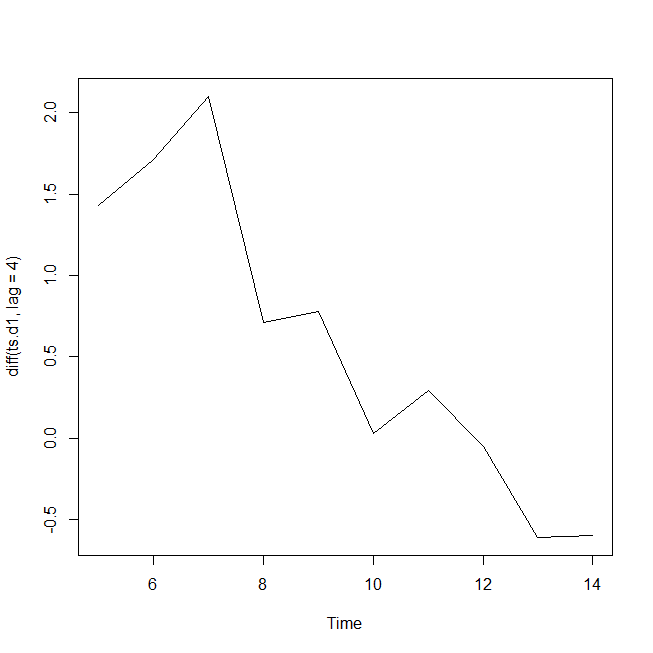
一週間前の五営業日とすると、
plot(diff(ts.d1,lag=5))
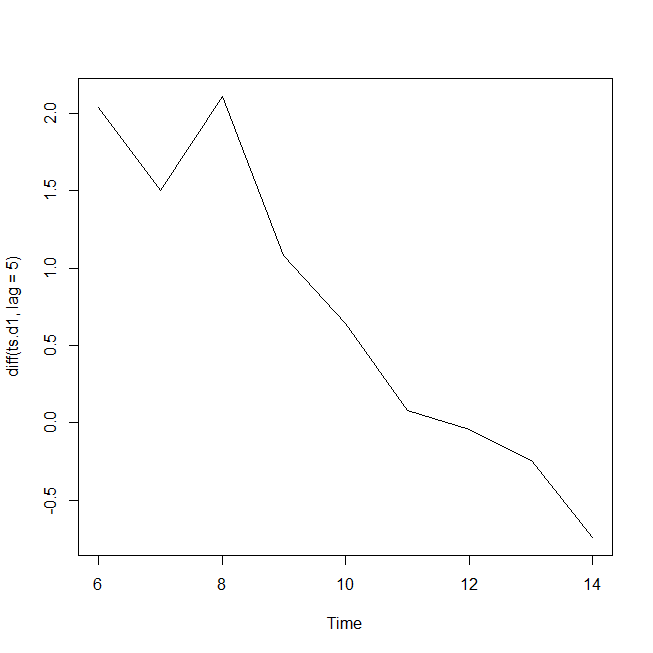
という感じで、差分を図示することができる。
時系列データの自己相関
時系列データのいくつか前のデータとの相関を自己相関と呼ぶ。
自己相関関数 autocorrelation function として、acf() がある。
acf() は図で結果を示してくれる。
acf(ts.d1)
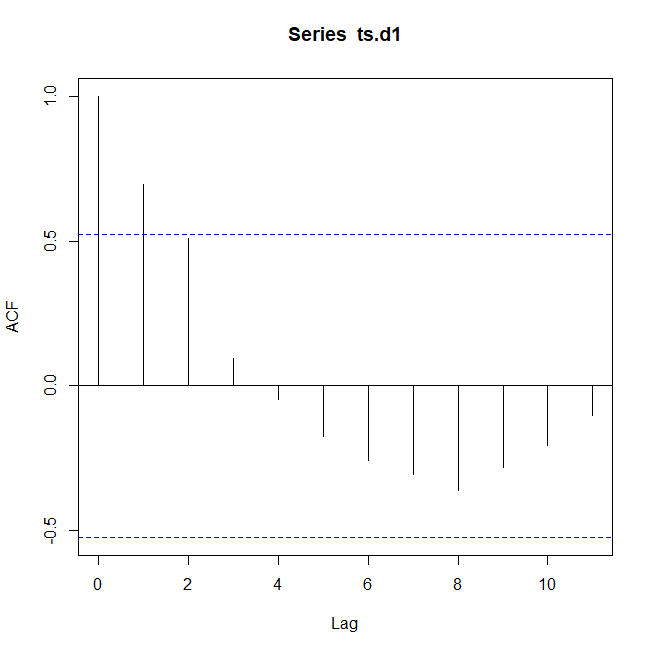
図によると、一つ前との自己相関が一番高いことがわかる。
また八つ前との自己相関が最も強く真逆であることもわかる。
時系列データがランダムウォークか何か傾向があるかの検定
時系列データがランダムにふらふらしているだけなのか、ある一定の傾向があるのかを検定する方法がPhillips-Perron検定だ。
R では、PP.test() が用意されている。
PP.test(ts.d1)
結果は以下の通り、ランダムであることは否定できない(帰無仮説はランダムウォークである)。
よって、何らかの傾向があるとはいいがたい。という結果になる。
> PP.test(ts.d1)
Phillips-Perron Unit Root Test
data: ts.d1
Dickey-Fuller = -0.93029, Truncation lag parameter = 2,
p-value = 0.9308
時系列データを用いて自己相関モデルに当てはめてみる
PP.test() で傾向はないとの結果であったが、そのまま時系列分析を進めてみる。
自己相関 AutoRegressive AR モデルを当てはめてみる。
統計ソフトRでは ar() という関数が使える。
ar1 <- ar(ts.d1)
結果は以下の通り。
三つ前までを使って、coefficients 3つで、次の値を予測できるという結果だ。
> ar1
Call:
ar(x = ts.d1)
Coefficients:
1 2 3
0.6883 0.4029 -0.5368
Order selected 3 sigma^2 estimated as 0.3143
時系列データの自己相関モデルでその後のデータを予測してみる
時系列データの自己相関モデル解析で得たモデルで、未来予測をしてみる。
10営業日あとまでを予測してみる。
pred1 <- predict(ar1,n.ahead=10)
結果は以下の通り。
予測値と標準誤差が算出される。
> pred1
$pred
Time Series:
Start = 15
End = 24
Frequency = 1
[1] 109.4391 109.3848 109.3565 109.3961 109.4411 109.5032 109.5429
[8] 109.5710 109.5730 109.5644
$se
Time Series:
Start = 15
End = 24
Frequency = 1
[1] 0.5606187 0.6805665 0.8394544 0.8612986 0.8701131 0.8759700
[7] 0.8846047 0.9051845 0.9141172 0.9194495
図示してみると以下のようになる。
UL <- pred1$pred+1.96*pred1$se
LL <- pred1$pred-1.96*pred1$se
ts.plot(ts.d1,pred1$pred)
空白の右側が予測値だ。
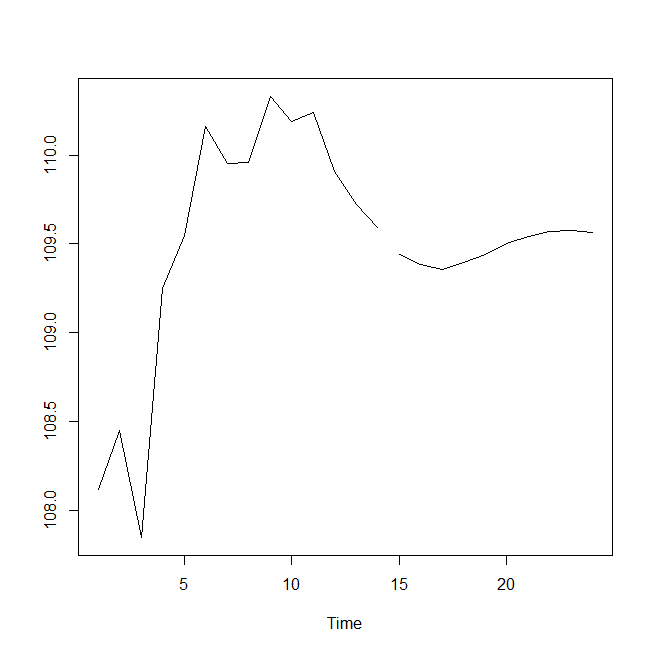
95%信頼区間も描き入れてみる。
ts.plot(ts.d1,pred1$pred,UL,LL,gpars=list(lty=c(1,2,3,3),col=c(1,2,4,4)))
青い点線が95%信頼区間の上限と下限。赤い破線が予測値だ。
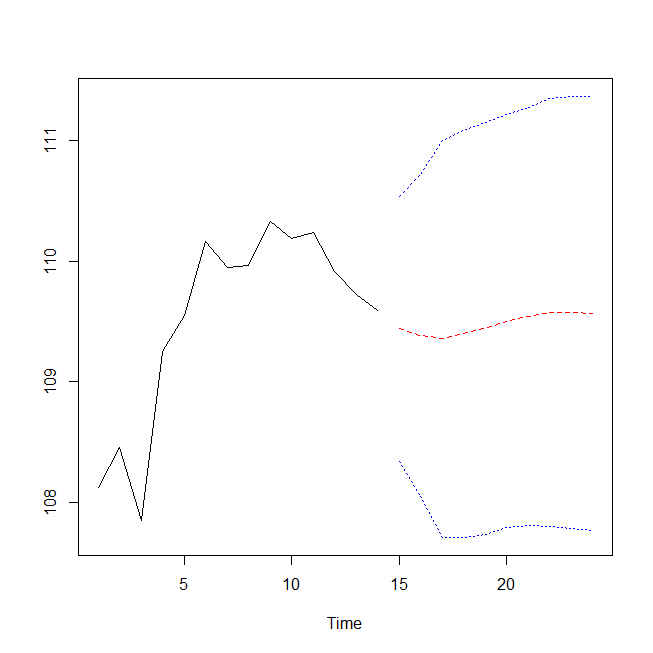
凡例を左の上に書き入れてみる。
legend("topleft",c("実測値","予測値","1.96xSE"),lty=c(1,2,3),col=c(1,2,4))
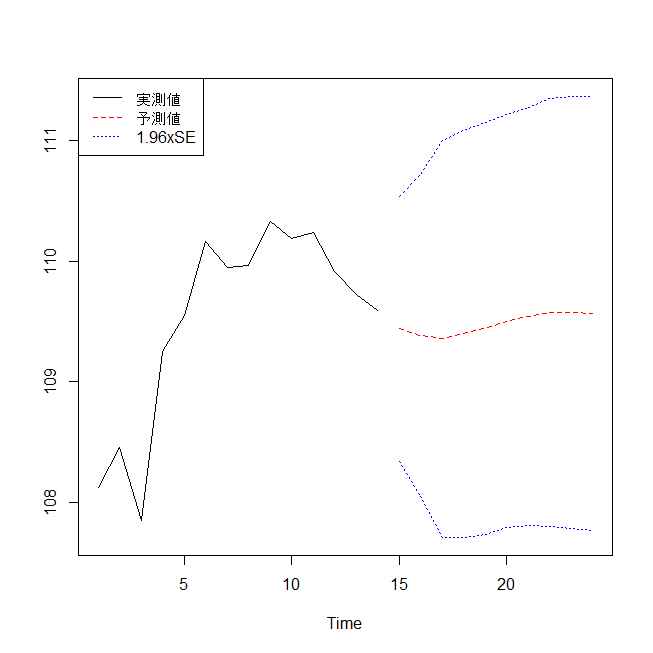
ドル円レートは、今後10営業日は、110円前後で推移しそうという予測が出た。
時系列データを自己相関と和分と移動平均で分析してみる
時系列データは、自己相関だけでなく、和分過程と移動平均を同時に考慮した autoregressive integrated moving average (ARIMA) によって分析される。
ARIMAの最適モデルを R では auto.arima() で見つけてくれる。
auto.arima() を使うには、forecast パッケージのインストールが必要だ。
インストールは最初の一回だけ必要になる。
install.packages("forecast")
auto.arima() を使用するときは、毎回 library() で呼び出す。
library(forecast)
auto.arima() を実行する。
trace=TRUE は計算過程を表示せよという指示。
stepwise=FALSE はステップで絞っていくのではなく総当たりでお願いという指示。
max.p, max.q はそれぞれ自己相関と移動平均のラグを10回まで検討してという指示。
aa1 <- auto.arima(ts.d1, trace=TRUE, stepwise=FALSE, max.p=10, max.q=10)
結果は以下の通り。
和分過程が1と出た。
データ同士の差分を取った値で分析するとよいという結果だ。
自己相関や移動平均は考慮不要という結果。
> aa1 <- auto.arima(ts.d1, trace=TRUE, stepwise=FALSE, max.p=10, max.q=10)
ARIMA(0,1,0) : 21.25859
ARIMA(0,1,0) with drift : 23.41377
ARIMA(0,1,1) : 23.8725
ARIMA(0,1,1) with drift : 26.41808
ARIMA(0,1,2) : 26.16093
ARIMA(0,1,2) with drift : 30.14083
ARIMA(0,1,3) : Inf
ARIMA(0,1,3) with drift : Inf
ARIMA(0,1,4) : Inf
ARIMA(0,1,4) with drift : Inf
ARIMA(1,1,0) : 23.73315
ARIMA(1,1,0) with drift : 26.21159
ARIMA(1,1,1) : 26.41278
ARIMA(1,1,1) with drift : 29.89844
ARIMA(1,1,2) : Inf
ARIMA(1,1,2) with drift : Inf
ARIMA(1,1,3) : Inf
ARIMA(1,1,3) with drift : Inf
ARIMA(1,1,4) : Inf
ARIMA(1,1,4) with drift : Inf
ARIMA(2,1,0) : 25.73261
ARIMA(2,1,0) with drift : 29.7048
ARIMA(2,1,1) : 29.81339
ARIMA(2,1,1) with drift : Inf
ARIMA(2,1,2) : Inf
ARIMA(2,1,2) with drift : Inf
ARIMA(2,1,3) : Inf
ARIMA(2,1,3) with drift : Inf
ARIMA(3,1,0) : 29.36422
ARIMA(3,1,0) with drift : 34.28436
ARIMA(3,1,1) : 34.9161
ARIMA(3,1,1) with drift : 41.6409
ARIMA(3,1,2) : Inf
ARIMA(3,1,2) with drift : Inf
ARIMA(4,1,0) : 34.85462
ARIMA(4,1,0) with drift : 41.49691
ARIMA(4,1,1) : 41.36168
ARIMA(4,1,1) with drift : 50.91271
Best model: ARIMA(0,1,0)
ベストモデルで10営業日先までを予測すると以下の通り。
fc1 <- forecast(aa1,h=10)
要するに同じ値としか推定できない。
PP.test() の結果、傾向があるとは言い難いという結論だったのと符合する。
> fc1
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
15 109.59 108.9475 110.2325 108.6073 110.5727
16 109.59 108.6813 110.4987 108.2003 110.9797
17 109.59 108.4771 110.7029 107.8880 111.2920
18 109.59 108.3049 110.8751 107.6247 111.5553
19 109.59 108.1533 111.0267 107.3927 111.7873
20 109.59 108.0161 111.1639 107.1830 111.9970
21 109.59 107.8900 111.2900 106.9901 112.1899
22 109.59 107.7727 111.4073 106.8106 112.3694
23 109.59 107.6624 111.5176 106.6420 112.5380
24 109.59 107.5582 111.6218 106.4826 112.6974
グラフにしてみるとだんだん95%信頼区間が広がっていくだけで何も面白みがない。
plot(fc1)
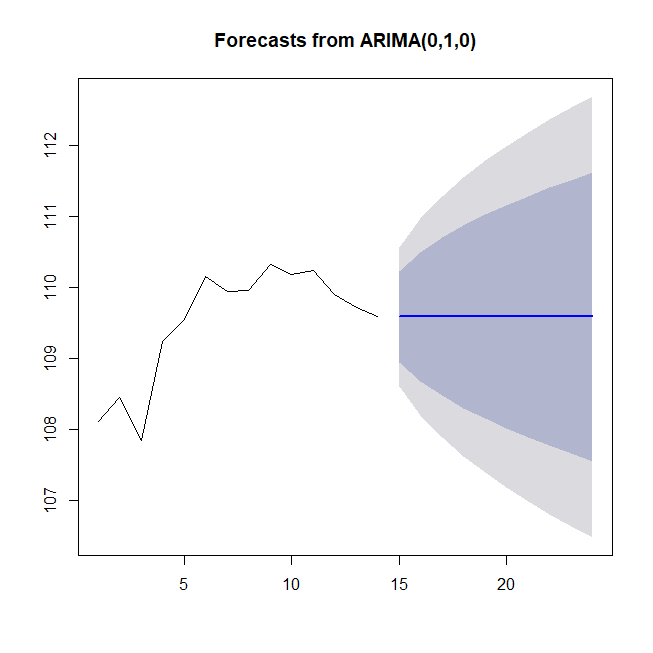
まとめ
時系列データがどういうものか、時系列データを図示したり、解析する方法を、Rを用いて解説した。
規則性があるデータは予測しやすいと想像する。
一方で、為替レートなど社会情勢によって左右される時系列データは、そう簡単には規則性を見出すのは難しいと感じる。
それでも時系列データ分析は、未来を予測するというとてもワクワクする要素を持つ。
参考になれば。









コメント