変化量の標準偏差を推定する場合に分散の加法性が成り立たないことについて

連続量の前後比較の際に、先行研究のデータ等から、変化量の標準偏差を知りたいと思うことがある。

しかし、たいていは変化量の標準偏差は掲載されていない。

前と後、別々の標準偏差から、変化量の標準偏差が分散の加法性を使って推定できないか？

変化量の標準偏差は掲載されていないことが多い

変化量、例えば、介入前後差の標準偏差が必要になることがある。

例えば、対応のあるｔ検定のサンプルサイズ計算の時には、前後差の標準偏差が必要だ。

しかし、論文にはたいてい介入前と介入後、別々の標準偏差が平均値と一緒に掲載されている。

それではその標準偏差から差の標準偏差を推定できないだろうか？

変化量の標準偏差推定に分散の加法性が使えないか？

分散の加法性とは？

分散の加法性とは、二つの変数を加えたり、変数間の差を取ったりした値の分散は、元の値の分散同士を足し合わせたものになるという性質だ。

変数 x+y の分散は、変数 x と変数 y の分散を足したものになる。

$$ V(x + y) = V(x) + V(y) $$

変数 x-y の分散も同じく、変数 x と変数 y の分散の和になる。

$$ V(x – y) = V(x) + V(y) $$

この法則を使えば、前後差 x-y の分散が、xの分散とyの分散から計算できるのではないか？

分散の加法性には条件がある

分散の加法性が成り立つには条件がある。

1. 不偏分散では成り立たず、標本分散でのみ成り立つ。
2. 変数 x と変数 y が独立である。

ということである。

つまり、介入前後のように同じ症例の場合、前後の測定値に相関があり、独立ではないため、分散の加法性は成り立たないのである。

分散の加法性が成り立つデータと成り立たないデータ

独立 2 群のデータの場合

独立 2 群で、2 群間に相関がない場合、測定値の散布図は以下のように完全にバラバラになる。

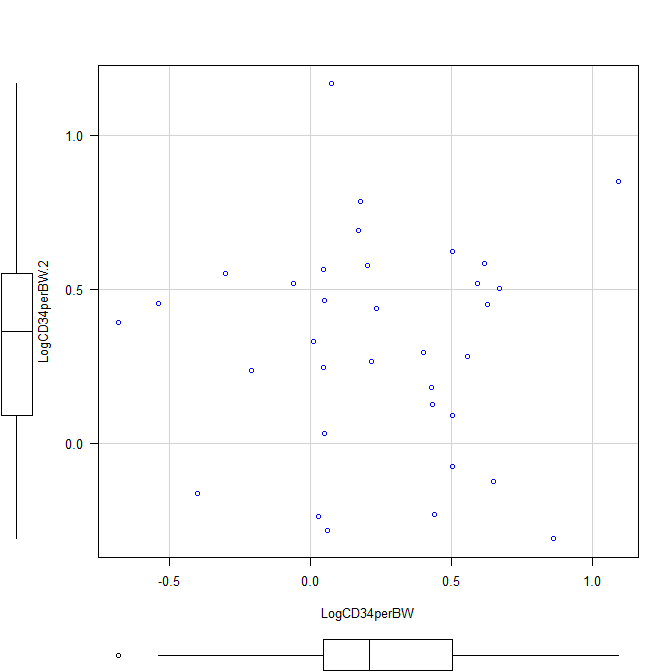
相関係数もゼロに限りなく近い。

このときに2変数の差と和の標本分散を計算すると以下のとおりである。

additionは x+y を意味している、difference は x-y である。

2つの標本分散の和と 和の標本分散 との差は、ほぼゼロになっている。

2つの標本分散の和と 差の標本分散 との差も、ほぼゼロである。

ちなみに、不偏分散では成り立たないとのことだが、不偏分散で計算しても、同様の結果であった。

「和の不偏分散」と「不偏分散の和」の差

「差の不偏分散」と「不偏分散の差」の差

対応のあるデータの場合

今回興味がある変化量などを計算する対応のあるデータの場合は、実際どのようになるか？

前後の変化量（対応のあるデータ）の間には相関がある。

同一人なので相関があることが普通である。

散布図で見ると、相関があることが示唆される。

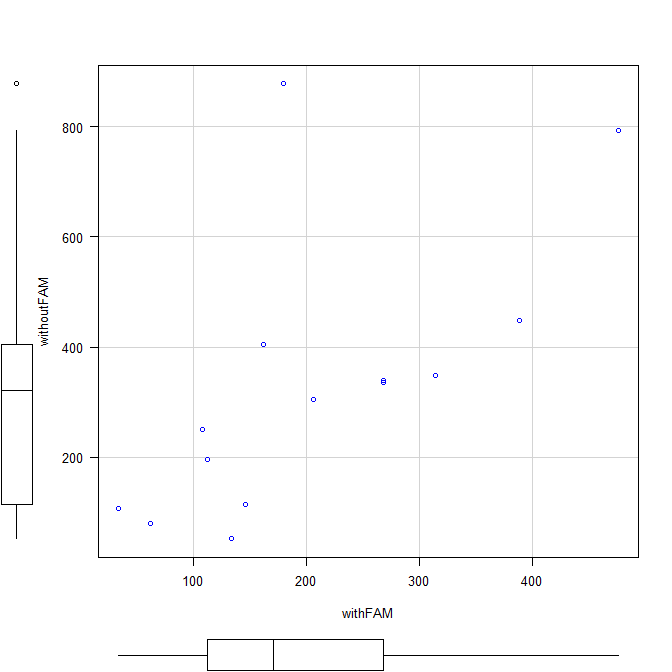
相関係数は0.642であり、ある程度相関があることがわかる。

このようなデータを用いて和と差の分散を求めてみると、以下のように計算される。

addFAMが和の分散、diffFAMが差の分散である。

和の分散、差の分散が大きく異なっていることがわかるし、ぱっと見でそれぞれの分散を足しても、和の分散、差の分散、どちらの分散にも近くないのがわかる。

つまり、対応のあるデータの場合、分散の加法性が成り立たず、前後の標準偏差から、差の標準偏差を推定することはできない。

まとめ

介入前後などの変化量や差の標準偏差を、前と後それぞれの標準偏差から推定したいことはよくあるが、分散の加法性を用いて推定することができないかと検討していくも、推定できないという結論になった。

EZR公式マニュアル

参考サイト

分散の加法性

参考動画