連続アウトカムの臨床予測モデル：予測精度を保証する内的・外的検証

臨床予測モデルは、医療現場で患者の将来を予測する強力なツールだ。特に血圧や血糖値のような連続データをアウトカムとするモデルは、病状の進行予測や治療効果の判定に役立つ。しかし、これらのモデルが実際に役立つためには、その予測能力が信頼できるものであることを確認する検証が不可欠だ。本記事では、連続アウトカムを扱う臨床予測モデルに焦点を当て、その内的検証と外的検証の重要性から具体的な方法、そしてその解釈までを詳しく解説する。

臨床予測モデルにおける内的検証と外的検証の概要

臨床予測モデルの検証は、開発されたモデルがどれほど正確に、そして汎用的に予測できるかを評価するプロセスだ。

内的検証は、モデルが開発された同じデータセット、あるいはそのサブセットを使ってモデルの性能を評価する。これは、モデルが学習データに過剰に適合していないか（過学習）、そして偶然の結果ではないかを確認するために行われる。内的検証によって、モデルの内部的な信頼性と安定性が保証される。

一方、外的検証は、モデル開発には一切使われていない独立した新しいデータセットを用いてモデルの性能を評価する。これは、モデルが開発された環境や特定の患者群だけでなく、異なる集団や状況においても同様の予測能力を発揮できるか、つまり汎用性があるかを確かめるために最も重要だ。外的検証をクリアして初めて、そのモデルの臨床応用への道が開かれる。

具体例で学ぶ内的検証と外的検証（Rを用いた計算例）

ここでは、患者の入院時の情報から退院時の HbA1c値（連続データ）を予測するモデルを例に、内的検証と外的検証の具体的な流れと評価指標を見ていこう。Rを用いたシミュレーションで解説する。

1. 必要なパッケージのインストールと読み込み

rmsパッケージを使用するため、まだインストールしていない場合は以下のコマンドでインストールしてほしい。

R スクリプト例：

# install.packages("rms")
# install.packages("dplyr") # データ操作のため
# install.packages("ggplot2") # 可視化のため
library(rms)
library(dplyr)
library(ggplot2)
set.seed(123) # 再現性のためのシード設定

2. ダミーデータの生成

ここでは、架空の「病院A」と「病院B」のデータを生成する。

• age: 年齢 (共変量1)
• bmi: BMI (共変量2)
• admission_glucose: 入院時血糖値 (共変量3)
• discharge_hba1c: 退院時HbA1c (アウトカム)

R スクリプト例：

# 病院Aのデータ（モデル開発用および内的検証用）
n_hospital_A <- 1000
hospital_A_data <- data.frame(
    age = round(rnorm(n_hospital_A, mean = 60, sd = 10)),
    bmi = round(rnorm(n_hospital_A, mean = 25, sd = 3), 1),
    admission_glucose = round(rnorm(n_hospital_A, mean = 150, sd = 30))
)
# 退院時HbA1cはage, bmi, admission_glucoseと乱数で生成
hospital_A_data$discharge_hba1c <- round(3.0 + 0.03 * hospital_A_data$age +
    0.05 * hospital_A_data$bmi +
    0.01 * hospital_A_data$admission_glucose +
    rnorm(n_hospital_A, mean = 0, sd = 0.8), 1)

# HbA1cは臨床上ありえそうな値範囲に調整
hospital_A_data$discharge_hba1c[hospital_A_data$discharge_hba1c < 4.0] <- 4.0
hospital_A_data$discharge_hba1c[hospital_A_data$discharge_hba1c > 12.0] <- 12.0


# 病院Bのデータ（外的検証用）
# 病院Aとは少し異なる特性を持つように平均値をわずかにずらす
set.seed(456) # 再現性のためのシード設定
n_hospital_B <- 300
hospital_B_data <- data.frame(
    age = round(rnorm(n_hospital_B, mean = 62, sd = 10)),
    bmi = round(rnorm(n_hospital_B, mean = 26, sd = 3), 1),
    admission_glucose = round(rnorm(n_hospital_B, mean = 160, sd = 30))
)

hospital_B_data$discharge_hba1c <- round(3.0 + 0.03 * hospital_B_data$age +
    0.05 * hospital_B_data$bmi +
    0.01 * hospital_B_data$admission_glucose +
    rnorm(n_hospital_B, mean = 0, sd = 0.8), 1)

hospital_B_data$discharge_hba1c[hospital_B_data$discharge_hba1c < 4.0] <- 4.0
hospital_B_data$discharge_hba1c[hospital_B_data$discharge_hba1c > 12.0] <- 12.0

# データの構造確認
str(hospital_A_data)
str(hospital_B_data)

3. モデル開発

rmsパッケージのdatadistとols関数を用いて線形回帰モデルを作成する。datadistは、データセットの変数分布に関する情報を設定し、後続のrms関数のヘルパーとして機能する。

R スクリプト例：

# モデル開発用のデータ（病院Aの全データを使用）
dd <- datadist(hospital_A_data)
options(datadist='dd')

# ols (Ordinary Least Squares) を用いて線形回帰モデルを開発
# 退院時HbA1cをage, bmi, admission_glucoseで予測
model_hba1c <- ols(discharge_hba1c ~ age + bmi + admission_glucose, data=hospital_A_data)
print(model_hba1c)

4. 内的検証（rms::validate関数を用いたブートストラップ検証）

rms::validate関数は、ブートストラップリサンプリングを用いてモデルの性能を評価し、特に楽観的バイアスを補正した評価指標を提供する。これにより、モデルが学習データにどれだけ過学習しているかを定量的に把握できる。

R スクリプト例：

# validate関数を用いた内的検証
# B=200 はブートストラップの繰り返し回数。通常はもっと大きい値（例: B=1000）を使用
# 実行には少し時間がかかる場合がある。
set.seed(456) # validate関数の再現性のためのシード設定
validation_results_internal <- validate(model_hba1c, method="boot", B=200) # Bはデモンストレーションのため小さく設定
print(validation_results_internal)

実行結果：

> print(validation_results_internal)
          index.orig training   test optimism index.corrected   n
R-square      0.2643   0.2671 0.2615   0.0056          0.2587 200
MSE           0.6311   0.6292 0.6335  -0.0043          0.6354 200
g             0.5370   0.5397 0.5356   0.0041          0.5329 200
Intercept     0.0000   0.0000 0.0485  -0.0485          0.0485 200
Slope         1.0000   1.0000 0.9933   0.0067          0.9933 200

内的検証結果の解釈：

ブートストラップ検証の結果に表示されている各指標の意味について説明する。

1. index.orig (Original Index)

• 意味: 元のデータセット全体でモデルを構築・評価した際の指標値
• 説明: 過学習の可能性がある「楽観的な」推定値。モデルが同じデータで構築され、同じデータで評価されているため、実際の性能よりも良く見積もられがち。

2. training (Training)

• 意味: 各ブートストラップサンプルでモデルを構築した際の指標値の平均
• 説明: ブートストラップサンプルでモデルを構築し、同じサンプルで評価した値の平均。これも過学習の影響を受けている。

3. test (Test)

• 意味: 各ブートストラップサンプルで構築したモデルを、元のデータセット全体で評価した際の指標値の平均
• 説明: より現実的な性能推定値。新しいデータでの性能をより正確に反映している。

4. optimism (Optimism)

• 意味: 楽観性バイアス（過学習の程度）
• 計算式: training - test
• 説明: この値が大きいほど、モデルが過学習していることを示す。理想的な値は0に近いことである。

5. index.corrected (Corrected Index)

• 意味: 楽観性バイアスを補正した指標値
• 計算式: index.orig - optimism
• 説明: 過学習の影響を取り除いた、より現実的なモデル性能の推定値。

結果の解釈例

R-square に関して

• index.orig: 0.2643 – 元のデータでの決定係数
• training: 0.2671 – ブートストラップサンプルでの平均決定係数
• test: 0.2615 – より現実的な性能推定
• optimism: 0.0056 – 楽観性バイアス（比較的小さい）
• index.corrected: 0.2587 – 補正後の決定係数

この場合、楽観性バイアス（0.0056）は比較的小さく、モデルの過学習は軽微であることが示されている。

5. 外的検証：予測精度とキャリブレーションの評価

外的検証では、開発に使用していない「病院B」のデータセットを用いてモデルの予測性能を評価する。ここでは、予測の正確さ（予測精度）と、予測値と実測値のずれ（キャリブレーション）の両面から評価する。

R スクリプト例：

# 病院Bのデータを用いて予測
predictions_external <- predict(model_hba1c, newdata = hospital_B_data)

# 実測値
actual_hba1c_external <- hospital_B_data$discharge_hba1c

### 予測精度 の評価 ###
# 1. RMSE (Root Mean Squared Error) の計算
rmse_external <- sqrt(mean((actual_hba1c_external - predictions_external)^2))
cat("\n--- 外的検証における予測精度の評価 ---\n")
cat("外的検証 RMSE:", rmse_external, "\n")

# 2. R2 (決定係数) の計算 - 外的検証用の修正版
# 外的検証では、予測値の平均ではなく実測値の平均を基準にする
# TSS (Total Sum of Squares) - 実測値の分散
tss_external <- sum((actual_hba1c_external - mean(actual_hba1c_external))^2)
# RSS (Residual Sum of Squares) - 予測誤差の二乗和
rss_external <- sum((actual_hba1c_external - predictions_external)^2)

# R²の計算
r_squared_external <- 1 - (rss_external / tss_external)
cat("外的検証 R2:", r_squared_external, "\n")

### キャリブレーション (Calibration) の評価 ###
# キャリブレーションは、予測値と実測値がどれだけ一致しているかを示す。
# 連続アウトカムの場合、予測値と実測値の間の系統的なバイアス（ずれ）がないかを確認する。
# 1. Calibration-in-the-large の評価（予測値の平均と実測値の平均の比較）
mean_predicted <- mean(predictions_external)
mean_actual <- mean(actual_hba1c_external)
cat("\n--- 外的検証におけるキャリブレーションの評価 ---\n")
cat("外的検証データにおける実測HbA1cの平均:", mean_actual, "\n")
cat("外的検証データにおける予測HbA1cの平均:", mean_predicted, "\n")
cat("平均の差 (実測 - 予測):", mean_actual - mean_predicted, "\n")
# 差が統計的に有意かどうかを検定することもできる (例: t.test)
# t.test(actual_hba1c_external, predictions_external, paired = FALSE) # 対応のないt検定

# 2. キャリブレーションプロット（視覚的評価と回帰分析による定量評価）
# 実測値を目的変数、予測値を説明変数とする線形回帰モデルを構築
# 理想的なキャリブレーションは、切片が0で傾きが1の直線 (y = x) だ。
calibration_model_external <- lm(actual_hba1c_external ~ predictions_external)
cat("\n--- 外的検証におけるキャリブレーション回帰モデルの要約 ---\n")
summary(calibration_model_external)
# キャリブレーションプロットの作成
plot_data_calibration <- data.frame(
    Actual = actual_hba1c_external,
    Predicted = predictions_external
)
ggplot(plot_data_calibration, aes(x = Predicted, y = Actual)) +
    geom_point(alpha = 0.6) +
    geom_smooth(method = "lm", se = FALSE, color = "blue", linetype = "solid") + # 回帰直線 (モデルのキャリブレーション)
    geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "red") + # 理想線 (y=x)
    labs(
        title = "外的検証: HbA1c キャリブレーションプロット (病院B)",
        x = "予測 HbA1c",
        y = "実測 HbA1c"
    ) +
    theme_minimal() +
    coord_equal(ratio = 1) # x軸とy軸のスケールを合わせる

---

実行結果：

> cat("\n--- 外的検証における予測精度の評価 ---\n")
--- 外的検証における予測精度の評価 ---
cat("外的検証 RMSE:", rmse_external, "\n")
> cat("外的検証 RMSE:", rmse_external, "\n")
外的検証 RMSE: 0.7457927 
> cat("外的検証 R2:", r_squared_external, "\n")
外的検証 R2: 0.2196644 

> cat("\n--- 外的検証におけるキャリブレーションの評価 ---\n")
--- 外的検証におけるキャリブレーションの評価 ---
> cat("外的検証データにおける実測HbA1cの平均:", mean_actual, "\n")
外的検証データにおける実測HbA1cの平均: 7.861 
> cat("外的検証データにおける予測HbA1cの平均:", mean_predicted, "\n")
外的検証データにおける予測HbA1cの平均: 7.789605 
> cat("平均の差 (実測 - 予測):", mean_actual - mean_predicted, "\n")
平均の差 (実測 - 予測): 0.07139512 

> cat("\n--- 外的検証におけるキャリブレーション回帰モデルの要約 ---\n")
--- 外的検証におけるキャリブレーション回帰モデルの要約 ---
> summary(calibration_model_external)

Call:
lm(formula = actual_hba1c_external ~ predictions_external)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.67026 -0.51287  0.00196  0.52809  2.24725 

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)    
(Intercept)           1.15231    0.70667   1.631    0.104    
predictions_external  0.86124    0.09055   9.511   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.7419 on 298 degrees of freedom
Multiple R-squared:  0.2329,    Adjusted R-squared:  0.2303 
F-statistic: 90.46 on 1 and 298 DF,  p-value: < 2.2e-16

> 

外的検証結果の解釈：

予測精度

• RMSE: 予測の平均的な誤差をアウトカムと同じ単位で示す。値が小さいほど予測精度が高いことを意味する。ただし、予測精度の良し悪しを判断する一般的な基準はない。
• R2: モデルがアウトカムの変動をどれだけ説明できているかを示す。1に近いほど説明力がある。
• 内的検証のR-square のindex.correctedと、外的検証のR2が大きく乖離しないことが重要だ。また、RMSEも同様に、両者で大きく異ならないことが望ましい（内部検証結果の MSE の index.corrected の平方根を計算する）。もし外的検証でこれらの指標が著しく悪化した場合、モデルの汎用性に問題がある可能性が高い。

キャリブレーション

• 外的検証データにおける実測HbA1cの平均と予測HbA1cの平均を比較する。これらの平均値が近いほど、モデル全体としての予測が偏っていないことを示す（約 0.07）
• calibration_model_externalのsummary()出力で、切片 (Intercept) の推定値とP値に注目する。P値が0.05未満の場合、切片が0と有意に異なることを意味し、平均的に予測が過大評価または過小評価されていることを示唆する（Intercept = 1.15, P=0.104 なので、大きく予測が外れているわけでもない）

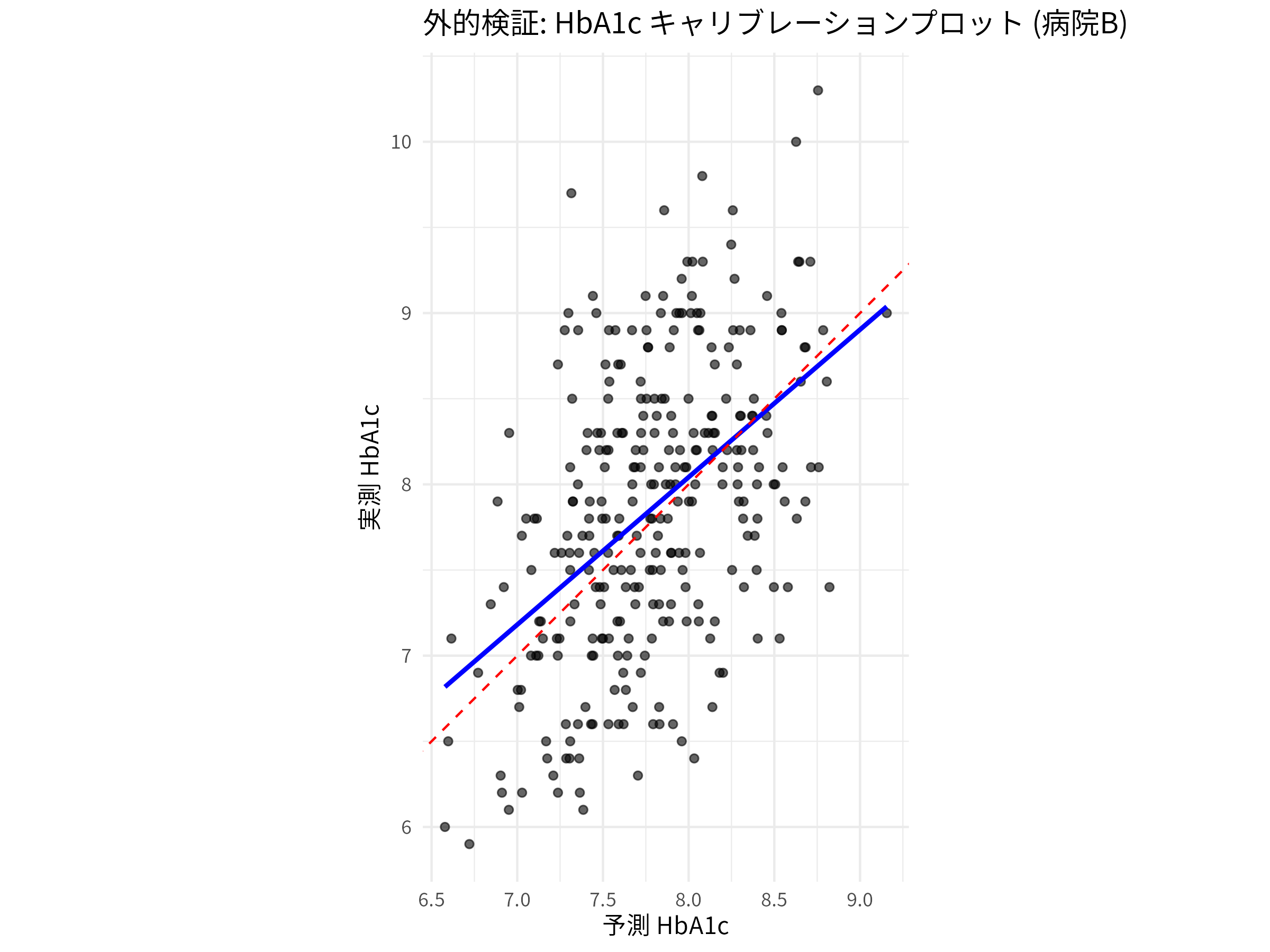
キャリブレーションプロット

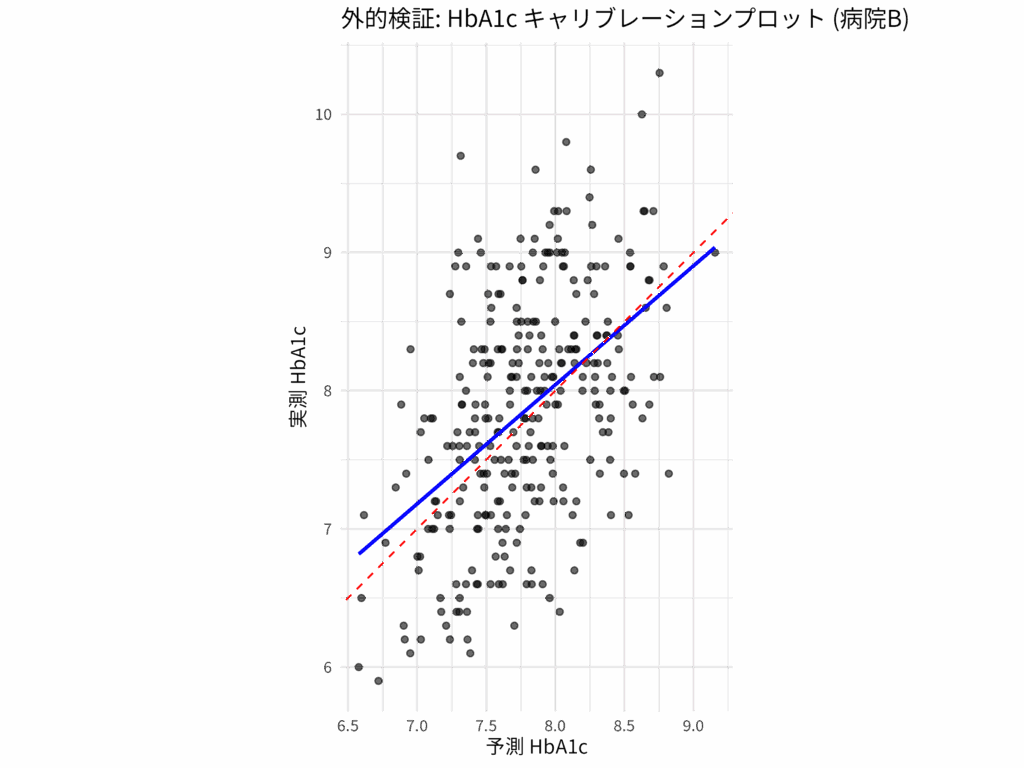
• 赤の破線 (y=x): 理想的なキャリブレーションを示す。予測値と実測値が完全に一致している状態。
• 青の実線 (回帰直線): モデルの実際のキャリブレーションを示す。この線が赤の破線にどれだけ近いかで、視覚的にキャリブレーションの良し悪しを判断できる。
• calibration_model_externalのsummary()出力で、predictions_external（つまり傾き）の推定値とP値にも注目する。P値が0.05未満で傾きが1と異なる場合、予測が極端すぎるか、控えめすぎる傾向があることを示す（predictions_external = 0.86, P < 0.001 であるので、予測が控えめすぎる傾向があるかもしれない）

総合的な判断

モデルが臨床現場で有用であるためには、予測精度が高く、かつキャリブレーションが良好であることが求められる。予測精度が高くてもキャリブレーションが悪ければ、個々の予測値が系統的にずれてしまい、臨床判断を誤る可能性がある。

この例では、rms::validateを使うことで、内的検証が単なるホールドアウト法よりも堅牢に行われ、ブートストラップによるバイアス補正が施された、より信頼性の高い内的性能指標が得られる。そして、独立したデータセットでの外的検証を行うことで、モデルの真の汎用性（予測精度とキャリブレーションの両面）が確認できる。

---

まとめ

臨床予測モデルは、その開発と同じくらい、あるいはそれ以上に検証プロセスが重要だ。特に連続アウトカムを扱うモデルでは、その予測の精度が患者の健康に直接影響を与えるため、慎重な評価が求められる。

内的検証は、モデルが過学習を起こしていないか、統計的に安定しているかを内部で確認するものであり、モデルの「基礎体力」を測るものだ。一方、外的検証は、モデルが開発された環境を超えて、様々な臨床現場でどれだけ通用するかを試すものであり、モデルの「実戦能力」を評価するものだ。

外的検証においては、予測の正確さを示す予測精度（RMSEやR2など）だけでなく、予測値と実測値がどれだけ一致しているかを示すキャリブレーション（平均値の比較やキャリブレーションプロットの切片・傾き）の評価も不可欠だ。これらの検証を通じて、モデルの限界を理解し、その信頼性を客観的に評価することが、臨床予測モデルを安全かつ有効に医療現場に導入するための不可欠なステップとなる。