R で階層的クラスタリングを行う方法。
階層的クラスタリングとは
さまざまな特徴を持った集団、たとえば米国50州を、特徴が似ている似ていないで近い・遠いを表現して部分集団(クラスター)に分けることを言う。
以下も参照のこと。

階層的クラスタリングのサンプルデータ
階層型クラスタリングを例示してみるサンプルデータはUSArrestsというデータで、1973年当時の米国犯罪データ。
先頭部分だけ少し見てみる。
各州の Murder, Assault, UrbanPop, Rape のデータが格納されている。
> head(USArrests)
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7
階層的クラスタリングは実際にどうするか?
まず距離計算をする
まず、州同士の距離計算をする。
dist()という関数を使う。
> dist1 <- dist(USArrests)
> dist1
Alabama Alaska Arizona Arkansas
Alaska 37.177009
Arizona 63.008333 46.592489
Arkansas 46.928137 77.197409 108.851918
California 55.524769 45.102217 23.194180 97.582017
Colorado 41.932565 66.475935 90.351148 36.734861
Connecticut 128.206942 159.406556 185.159526 85.028289
Delaware 16.806249 45.182961 58.616380 53.010376
Florida 102.001618 79.974496 41.654532 148.735739
Georgia 25.841827 57.030255 86.037957 25.586129
Hawaii 191.803050 221.193535 248.268967 147.775979
Idaho 116.761980 146.484982 176.817674 70.587038
途中で割愛するが、上記のような行列が、49行×50列続く。
これが距離行列だ。
次にクラスターに分ける
次にクラスターに分ける。
hclust()という関数を使う。
クラスターに分ける方法はいくつかある。
R のデフォルトではcomplete(完全リンク法)が用いられている。
> hclust1 <- hclust(dist1)
> hclust1
Call:
hclust(d = dist1)
Cluster method : complete
Distance : euclidean
Number of objects: 50
完全リンク法は、最も近い者同士がペアを作った後、そのどちらかと遠いほうの距離を採用して(50州の場合なら48個距離が選ばれる)、その中で最も近い者が次のレベルのクラスターになる。
詳しくは以下のリンク先を参照。
クラスタリング(スライド21枚目)
http://www.kamishima.net/archive/clustering.pdf
こちらもわかりやすい説明。
https://it-mint.com/2017/07/13/hierarchical-clustering-complete-linkage-1203.html
距離計算はユークリッド距離を用いている
ユークリッド距離 euclidean distanceは、二つの点の「差の二乗和の平方根」だ。
実際の計算は以下を参照。

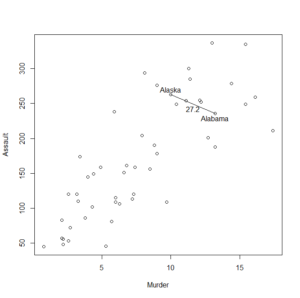
階層的クラスタリングの図示
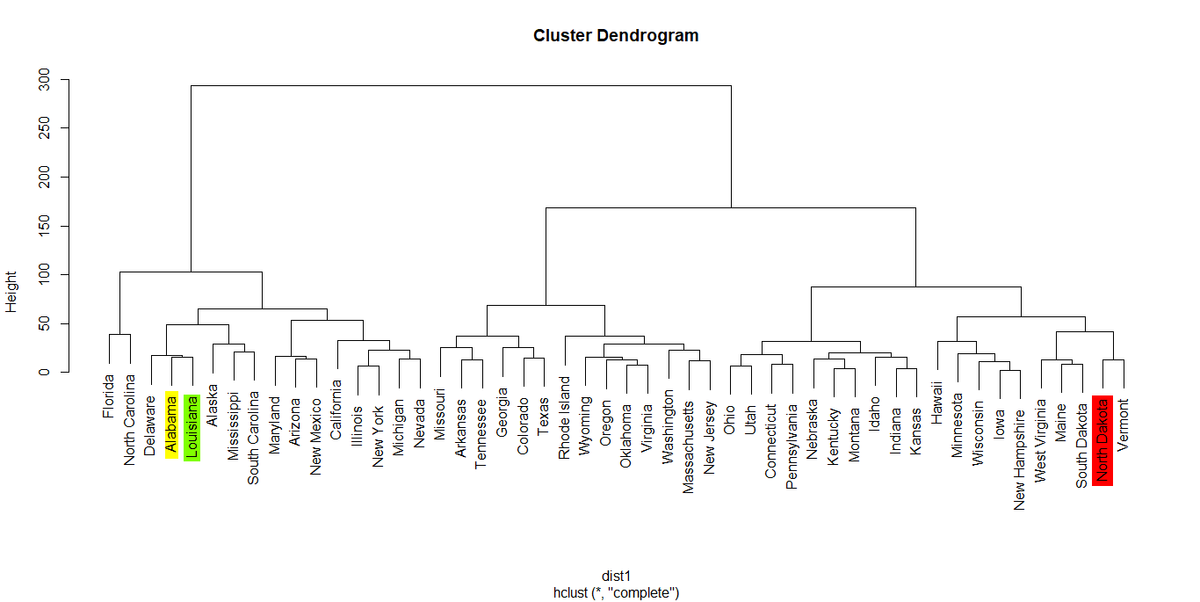
各点(例では各州)が近いのか、遠いのかを表示する図がある。
デンドログラムと呼ばれる。
日本語では樹形図とか樹状図と呼ばれる。
やはり図はわかりやすい。
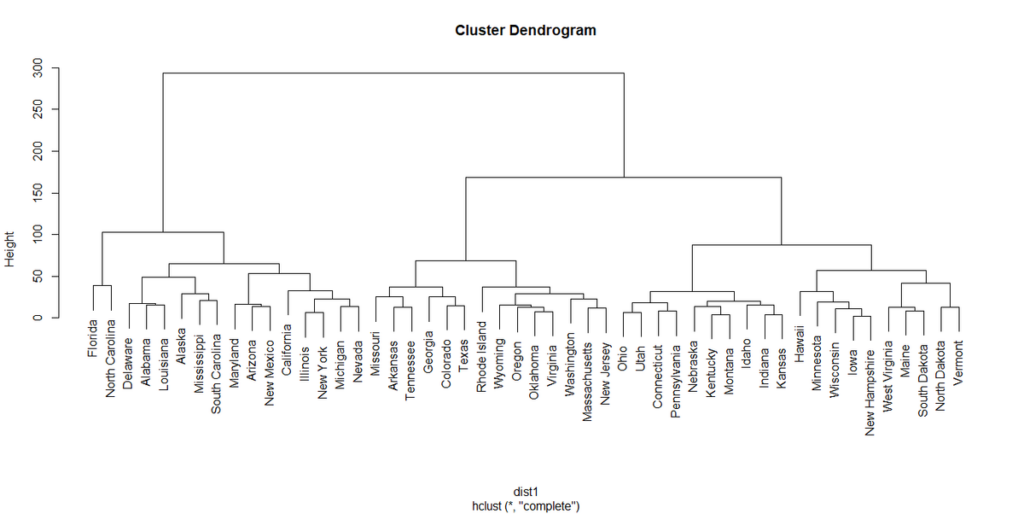
デフォルトでは名前が上下して同じレベルか違うレベルかが目視でわかるようになっている。
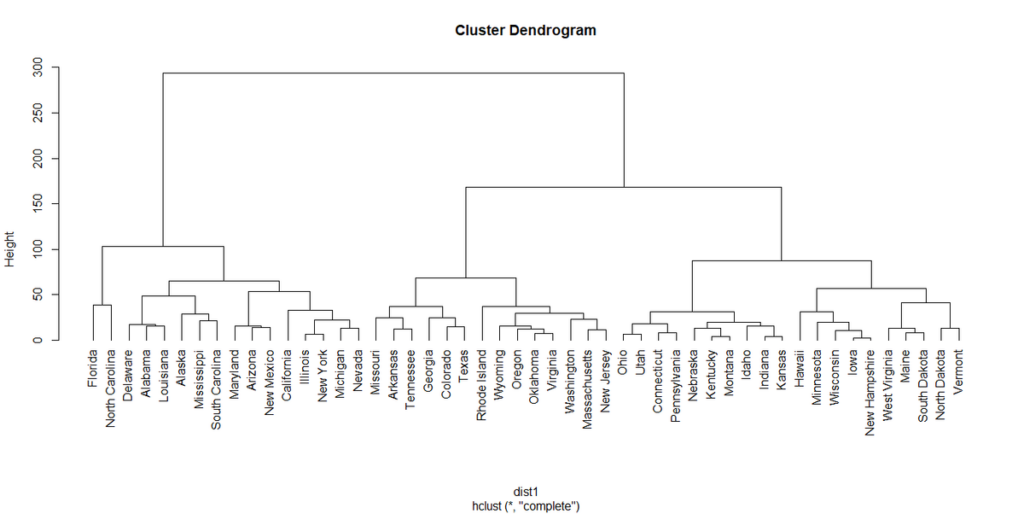
hang=-1とオプション指定すると、各州の名前が横一線に並ぶ表示になる。
plot(hclust1)
plot(hclust1,hang=-1)
デフォルトの表示
hang=-1を指定した時の表示
実際のユークリッド距離を計算してみる
例としてAlabamaとAlaska、AlabamaとArizonaの距離を計算してみると以下のようになる。
> head(USArrests)
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7
>
> #Alabama to Alaska
> sqrt(sum((USArrests[c(1,2),][1,]-USArrests[c(1,2),][2,])^2))
[1] 37.17701
> #Alabama to Arizona
> sqrt(sum((USArrests[c(1,3),][1,]-USArrests[c(1,3),][2,])^2))
[1] 63.00833
ユークリッド距離が最も近い州、最も遠い州は?
例としてAlabamaからユークリッド距離が最も近い州と最も遠い州を見てみる。
まず、Alabamaからそれぞれの州までの距離を計算する。
> alabama
Alaska Arizona Arkansas California Colorado
37.17701 63.00833 46.92814 55.52477 41.93256
Connecticut Delaware Florida Georgia Hawaii
128.20694 16.80625 102.00162 25.84183 191.80305
Idaho Illinois Indiana Iowa Kansas
116.76198 28.45488 123.34521 180.61010 121.51987
Kentucky Louisiana Maine Maryland Massachusetts
127.28417 15.45445 154.14529 64.99362 91.64851
Michigan Minnesota Mississippi Missouri Montana
28.48543 164.65096 27.39014 59.78829 127.39262
Nebraska Nevada New Hampshire New Jersey New Mexico
134.43697 37.43047 179.73620 83.24302 51.64349
New York North Carolina North Dakota Ohio Oklahoma
33.71083 101.96102 192.41614 117.38761 85.84870
Oregon Pennsylvania Rhode Island South Carolina South Dakota
78.38686 131.08509 70.33811 44.18292 151.08911
Tennessee Texas Utah Vermont Virginia
48.34760 41.56609 118.50270 190.37069 80.29533
Washington West Virginia Wisconsin Wyoming
92.82047 156.79241 183.77573 75.50709
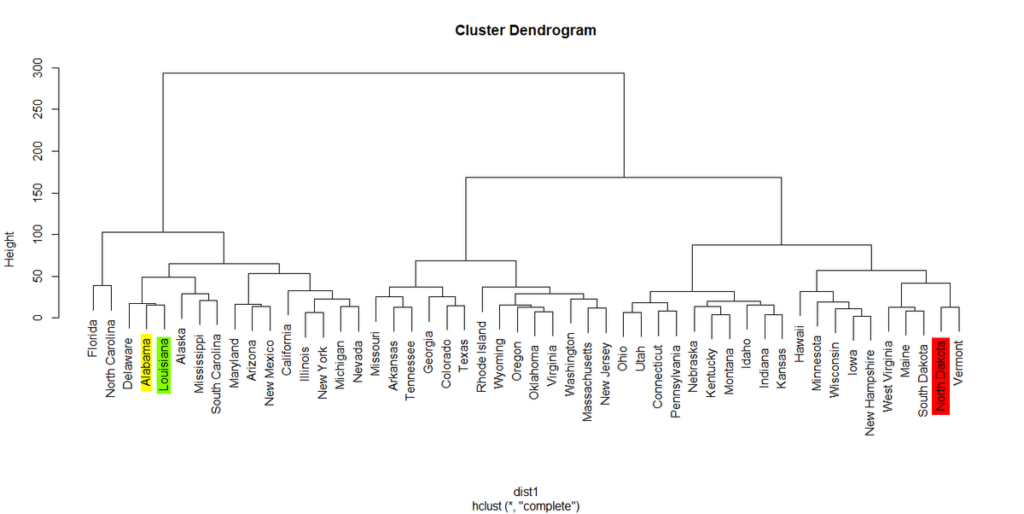
この中で最も近い(距離が小さい)州と最も遠い(距離が大きい)州を見つけてみる。
> min(alabama)
[1] 15.45445
> max(alabama)
[1] 192.4161
最小値は15.45445でLouisiana州であった。
最大値は192.4161でNorth Dakota州であった。
デンドログラムで見直してみると、Louisianaは隣に来ている州で、North Dakotaは遠く離れている場所に位置している。
このように表現される。
ちなみにAlabamaからみた物理的な距離を考えてみると、LouisianaはMississippiを挟んですぐ近くの州であるが、North Dakotaは遠く離れた中西部最北の州である。
まとめ
階層的クラスタリングは、いくつかの特徴を用いて、それらの特徴を持つ点同士の距離が近いか遠いかを使って、塊(クラスター)を作って、大まかな状況を把握する方法。
データの大まかな把握や仮説構築に有用な手法だ。
ぜひお試しあれ。








コメント
コメント一覧 (2件)
[…] R で階層的クラスタリングを行う方法 R で階層的クラスタリングを行う方法。 階層的クラスタリングとは […]
[…] R で階層的クラスタリングを行う方法 R で階層的クラスタリングを行う方法。 階層的クラスタリングとは […]