線形混合モデルのサンプルサイズ計算をシミュレーションで行う方法

---

研究計画を立てる際、避けて通れないのが目標症例数（サンプルサイズ）の決定である。特に、同一被験者を複数回測定する「縦断データ」や「反復測定データ」の場合、データの相関を考慮する必要があり、計算は一気に複雑化する。

本記事では、従来の数式による計算が困難な「線形混合モデル」において、R言語のシミュレーションを用いて論理的にサンプルサイズを導き出す手法を解説する。

---

線形混合モデルとは

線形混合モデル（Linear Mixed Model: LMM）とは、解析モデルの中に「固定効果」と「変量効果」を同時に組み込んだモデルのことである。

• 固定効果: 薬剤の種類や経過時間など、研究者が直接的に差を検証したい主たる要因である。
• 変量効果: 被験者ごとの個体差（ベースラインの高さや反応性の違い）など、データのバラツキとして処理すべき要因である。

縦断データでは「同一人物から得られたデータ同士は似通っている（独立していない）」という性質がある。このデータの依存関係を適切に処理できるのが、混合モデルの最大の特徴である。

---

サンプルサイズ計算が必要な局面

特に重要となるのが、小規模な研究で「有意差なし」という結果に終わった仮説を再検証する場合である。

有意差が出なかった原因が「本当に薬に効果がない」ためなのか、あるいは「サンプルサイズ不足による検出力（Power）の欠如」によるものなのかは、事前の計算なしには判別できない。特に治療効果の「変化の傾向（傾き）」の差を検出したい場合、単純な2群比較よりも多くの人数を要することが多いため、綿密な設計が不可欠である。

---

シミュレーションで行うべき理由

なぜ、一般的な統計ソフトの数式入力では不十分なのだろうか。

1. モデルの複雑性: 混合モデルには個体間・個体内の分散パラメータが多数存在し、単純な数式（t検定など）ではその構造を表現しきれない。
2. 非定型な測定点: 今回の例のように「0, 1, 3, 6ヶ月」といった不等間隔の測定スケジュールであっても、シミュレーションなら実態に即して柔軟に計算できる。
3. 現実的な条件の反映: 将来的に予測される脱落パターンの組み込みなど、実務に即したカスタマイズが可能である。

---

Rでの実践例：simrパッケージの活用

Rの simr パッケージを用いれば、構築したモデルをベースにモンテカルロ・シミュレーションを回し、検出力を算出できる。以下に、4時点での比較を想定したコードの骨格を示す。

1. モデル構造の定義

まず、ダミーデータを用いて「解析したいモデルの形」をRに教える。

if(!require(lme4)) install.packages("lme4")
if(!require(simr)) install.packages("simr")
library(lme4)
library(simr)

# 10人分のダミーデータ（0, 1, 3, 6ヶ月）
df <- expand.grid(time = c(0, 1, 3, 6), id = factor(1:10))
df$group <- factor(rep(c("New", "Old"), each = 20))
set.seed(123)
df$score <- rnorm(nrow(df)) # 収束を安定させるための微小ノイズ

model <- lmer(score ~ time * group + (1|id), data = df)

2. パラメータ（効果量とばらつき）の設定

ここが最も重要なステップである。先行研究などを参考に、「最低限これくらいの差は検出したい」という数値をモデルに注入する。すでにデータがある場合は、そのデータに合わせて設定するのがよい。

# 固定効果（係数）の設定
# 6ヶ月時点で新薬が従来薬より「1.2」スコアが改善すると仮定（傾きの差 = 1.2/6 = 0.2）
fixef(model) <- c(
  "(Intercept)" = 10,    # ベースラインの平均点
  "time" = -0.1,         # 従来薬の自然な変化
  "groupOld" = 0,        # 開始時点の群間差
  "time:groupOld" = 0.2  # 【重要】検出したい「傾きの差」
)

# 誤差（ばらつき）の設定
sigma(model) <- 1.2        # 残差（個体内の変動）
VarCorr(model) <- list(id = 0.8^2) # 個体差（ランダムインターセプトの分散）

3. サンプルサイズの拡張と試行

人数を増やしながら、80%の検出力を超えるポイントを探る。

# 100人まで拡張してパワーカーブを描画
model_ext <- extend(model, along = "id", n = 100)
pc <- powerCurve(model_ext, test = fixed("time:groupOld", "t"), along = "id", nsim = 100)
plot(pc)

---

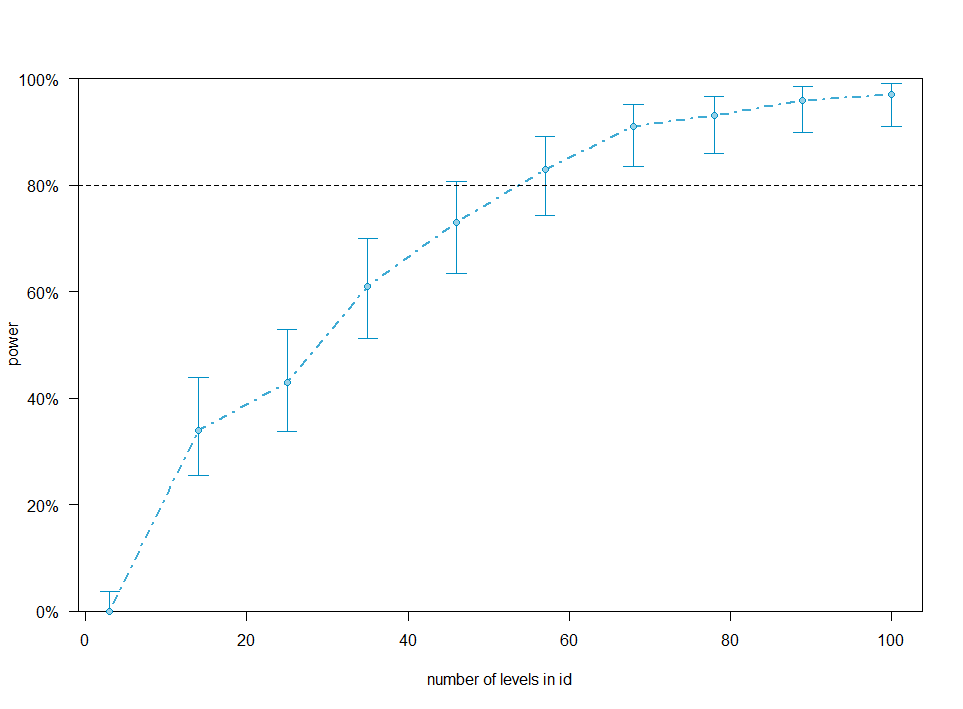
結果の解釈

シミュレーションを実行すると、サンプルサイズ（横軸）と検出力（縦軸）の関係を示す「パワーカーブ」が得られる。

• 青い点（点推定値）: 各サンプルサイズにおけるシミュレーション上の平均的な検出力である。
• エラーバー（95%信頼区間）: 試行回数に基づく推定の幅である。

実務的には、「信頼区間の下限が目標とする検出力（一般に80%）を安定して上回るポイント」（上記の場合は id ベース、つまり両群で 65 ～ 70 例）を必要サンプルサイズとして採用するのが、最も堅実な判断である。

---

ドロップアウトを考慮した実務的な判断

シミュレーションで算出された $n$ は、解析対象となる「有効データ数」であることに注意が必要である。

実際の臨床研究では必ず脱落（ドロップアウト）が発生するため、以下の計算で最終的な募集人数を決定する。

1. 予測脱落率の算出: 先行研究に基づき、最終測定時点での脱落率を予測する（例：20%）。
2. 目標募集人数の設定: 必要サンプルサイズ ÷ (1 - 脱落率)。
   • 例：計算上の必要数が70人の場合、$70 \div 0.8 = 87.5$。よって、90人程度をリクルートするのが妥当である。

---

まとめ

線形混合モデルのサンプルサイズ計算において、シミュレーションは極めて強力な武器となる。

• simr 等のツールを活用し、実態に即したデータ構造で試行すること。
• 単なる平均値の差ではなく、「時間の経過に伴う群間差（相互作用）」をターゲットに据えること。
• パワーカーブのエラーバーの下限を確認し、余裕を持った計画を立てること。

論理的な裏付けに基づくサンプルサイズ設計こそが、研究の価値を決定づける重要なプロセスである。

おすすめ書籍

誰も教えてくれなかった　医療統計の使い分け〜迷いやすい解析手法の選び方が，Rで実感しながらわかる！

---