Begg検定、Egger検定、Macaskill検定という出版バイアスの検定方法の解説。
出版バイアス検定のための個々の研究データ
出版バイアスを検定するためのサンプルデータは以下の通り。
a <- c(3,7,5,102,28,4,98,60,25,138,64,45,9,57,25,65,17)
n1 <- c(38,114,69,1533,355,59,945,632,278,1916,873,263,291,858,154,1195,298)
c <- c(3,14,11,127,27,6,152,48,37,188,52,47,16,45,31,62,34)
n0 <- c(39,116,93,1520,365,52,939,471,282,1921,583,266,293,883,147,1200,309)
dat <- data.frame(a,n1,c,n0)
Rのmetaforパッケージを使う。
metaforパッケージは初回だけインストールが必要。
install.packages("metafor")
metaforパッケージのescalc()で、個々の研究の推定値と分散を計算する。
このデータでは推定値はオッズ比。
measure=で指定する。
推定値yiと分散viが計算される。
統合オッズ比と95%信頼区間は、制限付き最尤推定量(REML)で計算する。
library(metafor)
dat.escalc <- escalc(measure="OR", ai=a, n1i=n1, ci=c, n2i=n0, data=dat)
res.reml <- rma.uni(yi, vi, method="REML", data=dat.escalc)
ファンネルプロットを書くと以下の通りだ。
funnel(res.reml)
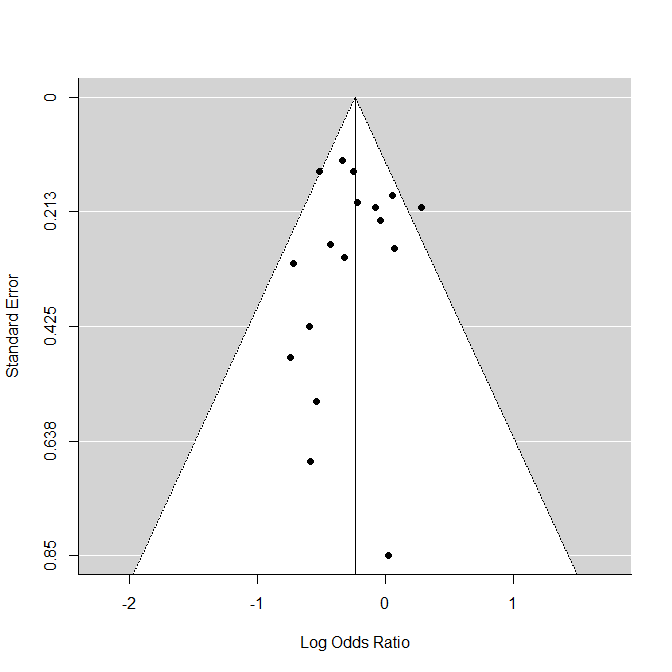
ファンネルプロットについては以下も参照。
yiとviが計算されれば、オッズ比以外の推定値の統合も可能だ。
平均値の差も統合可能。
平均値の差のメタアナリシスはこちらを参照。
Begg検定 出版バイアスを順位相関で検出する方法
出版バイアスの検定として一つ目は、Beggの順位相関という方法を実施してみる。
分散($ s_i^2$ スクリプトでは si2 とする)の逆数を重みにした推定値の重みづけ平均($ \hat{\theta}$ スクリプト中では theta とする)を計算する。
Rのスクリプトは以下の通り。
thetai <- dat.escalc$yi
si2 <- dat.escalc$vi
theta <- sum(thetai/si2)/sum(1/si2)
si2star <- si2 - 1/sum(1/si2)
si.star <- sqrt(si2star)
ti <- (thetai-theta)/si.star
各試験の推定値の標準偏差(つまり標準誤差)を計算する。
分散($ s_i^2$)から重みの合計の逆数を引いたものの平方根が各試験の標準誤差 $ s_i^*$ だ。
$ \hat{\theta} $ と $ s_i^* $ で、各試験の推定値 $ \hat{\theta}_i $ を標準化したものが、$ t_i $ スクリプト中では tiである。
$ t_i $ と $ s_i^2 $ 間のKendallの順位相関が0かどうかを検定する。
つまり、標準化した各試験の推定値と、各試験の分散が相関しているのかどうかを検定する。
帰無仮説が棄却できず、Kendallの順位相関が0であることを否定できなければ、出版バイアスはないと判断してよい。
Kendallの順位相関はこちらも参照。
統計学的有意かどうかは有意水準10%を用いる。
メタアナリシスの対象となる研究数が少ないため、検出力が低いからだ。
有意水準10%は他の2つの方法も同様だ。
$ t_i $ と$ s_i^2 $ の散布図を描いてみる。
plot(ti, si2)
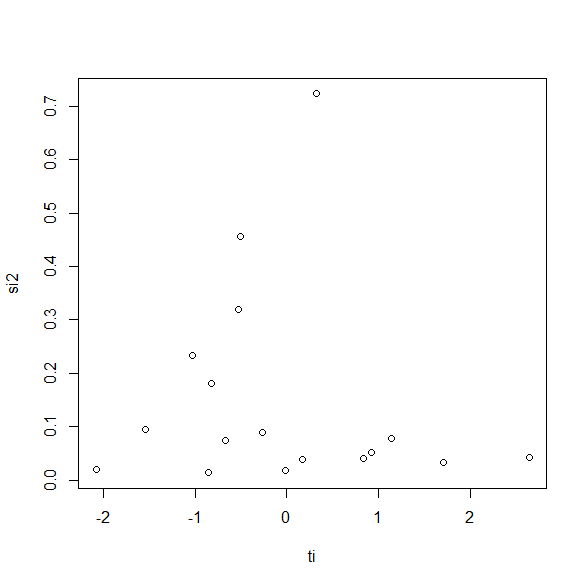
Kendallの順位相関を計算する。
cor.test(ti, si2, method="kendall")
相関係数は-0.059でp値は0.777で、相関係数が0であるという帰無仮説を棄却できない。
つまり相関係数がゼロであることを否定できない。
標準化された推定値と各研究の重みの逆数(分散)の間には相関がなく、研究結果や精度によるバイアスは検出されなかった。
> cor.test(ti, si2, method="kendall")
Kendall's rank correlation tau
data: ti and si2
T = 64, p-value = 0.7765
alternative hypothesis: true tau is not equal to 0
sample estimates:
tau
-0.05882353
metaforパッケージのranktest()を使うとずっと簡単。
ranktest(res.reml)
メタアナリシスの計算結果が格納されているオブジェクト(ここではres.reml)があれば、推定値の重みづけ平均や、各研究の標準偏差、推定値の標準化の計算は全く不要で、一瞬で結果が得られる。
> ranktest(res.reml)
Rank Correlation Test for Funnel Plot Asymmetry
Kendall's tau = -0.0588, p = 0.7765
Egger検定 出版バイアスを回帰分析で検出する方法
Eggerの方法は、以下の回帰モデルを用いる。
$$ \left( \frac{\hat{\theta}_i}{s_i} \right) = \alpha + \beta \left( \frac{1}{s_i} \right) + 誤差 $$
帰無仮説の元では、ファンネルプロットが左右対称形ならば、この回帰式は原点を通り(α= 0)、傾きは統合推定値に等しく($ \hat{\beta} = \hat{\theta} $)なるので、α = 0 を検定する。
前節で使った変数を引き続き使う。
si <- sqrt(si2)
theta.si <- thetai/si
inv.si <- 1/si
線形モデルlm()で、上記回帰モデルを推定する。
res.theta.si <- lm(theta.si ~ inv.si)
summary(res.theta.si)
結果は以下の通り。
(Intercept)の行が α = 0 の検定結果。
p値が0.817で、ゼロを否定することはできない。
ゆえにファンネルプロットは左右対称形である帰無仮説は棄却されず、出版バイアスがある可能性は低いと言える。
> summary(res.theta.si)
Call:
lm(formula = theta.si ~ inv.si)
Residuals:
Min 1Q Median 3Q Max
-1.9909 -0.7373 -0.2046 0.8214 2.5698
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.1518 0.6463 -0.235 0.817
inv.si -0.2152 0.1395 -1.543 0.144
Residual standard error: 1.194 on 15 degrees of freedom
Multiple R-squared: 0.1369, Adjusted R-squared: 0.07937
F-statistic: 2.379 on 1 and 15 DF, p-value: 0.1438
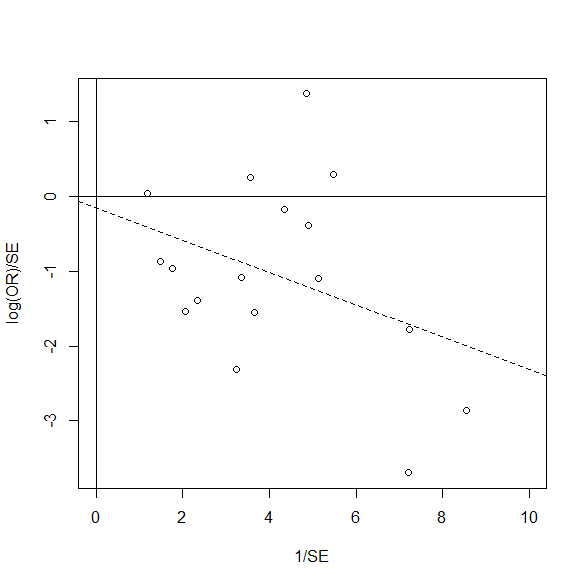
各研究をプロットして、回帰直線を引いてみる。
回帰直線(破線)はほぼ原点を通っていることがわかる。
plot(theta.si ~ inv.si, xlab="1/SE", ylab="log(OR)/SE", xlim=c(0,10))
abline(h=0, v=0, lty=1)
abline(res.theta.si, lty=2)
metaforパッケージのregtest()を使うと簡単に計算できる。
regtest(res.reml, model="lm")
結果は以下の通り。
t値とp値が、regtest()を使わない結果と一致しているのがわかる。
> regtest(res.reml, model="lm")
Regression Test for Funnel Plot Asymmetry
Model: weighted regression with multiplicative dispersion
Predictor: standard error
Test for Funnel Plot Asymmetry: t = -0.2349, df = 15, p = 0.8175
Limit Estimate (as sei -> 0): b = -0.2152 (CI: -0.5126, 0.0822)
ちなみに、研究間に無視できない異質性が検出された場合、変量効果モデルで統合することになるが、そのときはEggerの方法も変量効果モデルで実施するとよい。
今回の例題はすでにREMLを用いて変量効果モデルで統合しているので、解析結果のオブジェクトはそのままでOK。
先ほど model = “lm” というオプションを入れたが、そのオプションを入れないと、変量効果モデルの結果になる。
> regtest(res.reml)
Regression Test for Funnel Plot Asymmetry
Model: mixed-effects meta-regression model
Predictor: standard error
Test for Funnel Plot Asymmetry: z = -0.7411, p = 0.4586
Limit Estimate (as sei -> 0): b = -0.1311 (CI: -0.4408, 0.1787)
有意確率は p=0.4586 とやや低下したが、有意水準10%として、統計学的有意ではなく、出版バイアスがあるとは言えないという結果となる。
Macaskill検定 出版バイアスを回帰分析で検出する方法
Macaskillの方法は、以下の回帰モデルを用いた重みづけ回帰分析だ。
$$ \hat{\theta}_i = \alpha + \beta n_i + 誤差 $$
推定値 $ \hat{\theta}_i $ をサンプルサイズ $ n_i $ で予測する回帰式だ。
重みは分散の逆数を用いる。
ファンネルプロット回帰法とも呼ばれる。
もし出版バイアスがあるなら、サンプルサイズが小さい研究ほど、研究結果の推定値が大きいほうに偏るはず。
これは、真の推定値が正の場合である。
負の場合は、小さいほうに偏る。
サンプルサイズが小さいと統計学的有意になりにくく、推定値が大きいがために統計学的有意になったという偏った研究のみが採択されている可能性がある。
この偏りを検出するわけだ。
ファンネルプロットが左右対称形なら、回帰式の傾きがゼロになる。
すなわち帰無仮説は β = 0 だ。
各研究のサンプルサイズ $ n_i $ を計算して、先ほどの回帰モデルで β を推定する。
ni <- dat$n1+dat$n0
res.theta.n <- lm(thetai ~ ni, weights=1/dat.escalc$vi)
summary(res.theta.n)
結果は以下の通り。
> summary(res.theta.n)
Call:
lm(formula = thetai ~ ni, weights = 1/dat.escalc$vi)
Weighted Residuals:
Min 1Q Median 3Q Max
-1.9432 -0.7026 -0.3085 0.7728 2.5467
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.269e-01 1.250e-01 -1.816 0.0895 .
ni -8.469e-06 5.209e-05 -0.163 0.8730
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.196 on 15 degrees of freedom
Multiple R-squared: 0.001759, Adjusted R-squared: -0.06479
F-statistic: 0.02643 on 1 and 15 DF, p-value: 0.873
niのCoefficientのEstimateを見るとほぼゼロ。
p値(Pr(>|t|))を見ると0.873で、β = 0 の帰無仮説を棄却できない。
つまり、β = 0 が否定できない。
すなわち出版バイアスがある可能性は低いと考えられる。
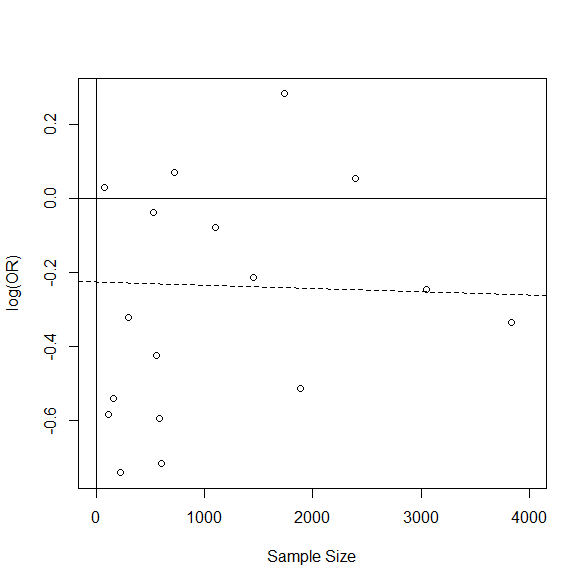
各研究をプロットして、回帰直線を引いてみる。
傾きがほぼゼロであることが確認できる。
出版バイアスがあるとは断定できない。
plot(thetai ~ ni, xlab="Sample Size", ylab="log(OR)", xlim=c(0,4000))
abline(h=0, v=0, lty=1)
abline(res.theta.n, lty=2)
metaforパッケージのregtest()を使うとこちらも簡単だ。
regtest(res.reml, model="lm", predictor="ni")
結果は以下の通りで、
t値とp値が、regtest()を使わない方法と一致している。
> regtest(res.reml, model="lm", predictor="ni")
Regression Test for Funnel Plot Asymmetry
model: weighted regression with multiplicative dispersion
predictor: sample size
test for funnel plot asymmetry: t = -0.1626, df = 15, p = 0.8730
まとめ
出版バイアスの有無を検討する方法として、Beggの方法、Eggerの方法、Macaskillの方法を実施してみた。
ファンネルプロットと比べて数値と統計学的検定で判断できるので、白黒つけやすくわかりやすいが、ファンネルプロットと合わせて総合的に判断する必要がある。
Rのmetaforパッケージの関数を使うと簡単に計算できる。
何らか参考になれば幸い。
参考書籍
丹後俊郎著 メタ・アナリシス入門 朝倉書店
6. Publication biasへの挑戦
6.1 公表バイアスの検出

新版も出てる









コメント