臨床研究や心理学、社会調査などで「非常に満足〜非常に不満」といった評価尺度の変化を調べたい場面は多い。このようなデータを正しく解析するには順序ロジスティック回帰が適しているが、同じ人に繰り返し測定を行う場合は、さらに一般化線形混合モデル(GLMM)という高度な枠組みが必要になる。
しかし、このモデルは構造が複雑なため、標準的なソフトではサンプルサイズ計算ができない。本記事では、Rを用いたモンテカルロ・シミュレーションによって、根拠のあるサンプルサイズを導き出す方法を解説する。
一般化線形混合モデル(順序ロジスティック)とは
このモデルは、以下の2つの要素を組み合わせたものである。
- 順序ロジスティック: 「非常に不満、やや不満、やや満足、非常に満足」のように、数値としての意味(間隔)は厳密ではないが、順序には明確な意味があるデータを扱う。
- 混合モデル: 「同じ被験者に3回測定する」といった、データ間の相関(個人の回答の癖など)を「変量効果」として考慮する。
サンプルサイズ計算の必要性
特に観察研究において、結果が「有意ではなかった($p \ge 0.05$)」となった場合、それが「本当に差がない」のか「人数が足りなくて検出できなかっただけ」なのかを区別しなくてはならない。あらかじめ検定力分析を行い、必要な人数を確保しておくことは、研究の妥当性を証明するために非常に重要である。
なぜ、シミュレーションが必要なのか
通常のt検定などと違い、順序混合モデルには「複数の境界点(閾値)」や「個人内の相関」が含まれる。これらが複雑に絡み合うため、単純な数式(公式)でサンプルサイズを算出することができない。
そこで、「コンピュータ上で仮想の実験を数千回繰り返し、何回有意な結果が得られるか」を直接カウントするシミュレーション手法が、現在最も信頼できる解決策となる。
R でのシミュレーションの実例
以下に、複数のサンプルサイズ(30〜120名)に対して検定力を一括計算し、グラフ化するRコードを掲載する。4 件法のアウトカムで、2 群 × 3 回測定(ベースライン、1か月後、3か月後など)を想定している。
# --- 0. パッケージの確認と読み込み ---
if (!require("ordinal")) install.packages("ordinal")
if (!require("dplyr")) install.packages("dplyr")
if (!require("ggplot2")) install.packages("ggplot2")
library(ordinal)
library(dplyr)
library(ggplot2)
# --- 1. 基本設定 ---
# 検証したい1群あたりの人数リスト
n_list <- c(30, 50, 80, 100, 120)
n_time <- 3
# 信頼性を担保するため、最終的には1000回を推奨する
iterations <- 100
set.seed(123)
# 効果量とバラツキの設定
beta_interaction <- 0.8 # 介入による改善効果(交互作用)
sigma_u <- 1.0 # 個人差の大きさ
thresholds <- c(-1.5, 0, 1.5) # 4件法の境界点
# --- 2. シミュレーション用関数 ---
get_power <- function(n_target) {
message(paste("計算中: n =", n_target, "..."))
results <- replicate(iterations, {
# 仮想データの生成
df <- expand.grid(id = 1:(n_target * 2), time = 0:(n_time - 1)) %>%
mutate(
group = ifelse(id <= n_target, 0, 1),
u_i = rep(rnorm(n_target * 2, 0, sigma_u), each = n_time),
eta = 0.5 * time + beta_interaction * (group * time) + u_i
)
df$y <- as.factor(sapply(df$eta, function(e) {
latent <- e + rlogis(1)
if(latent <= thresholds[1]) return(1) # 非常に不満
if(latent <= thresholds[2]) return(2) # やや不満
if(latent <= thresholds[3]) return(3) # やや満足
return(4) # 非常に満足
}))
# モデル適合と検定
tryCatch({
mod <- clmm(y ~ group * time + (1|id), data = df)
p_val <- summary(mod)$coefficients["group:time", "Pr(>|z|)"]
return(p_val < 0.05)
}, error = function(e) return(NA))
})
return(mean(results, na.rm = TRUE))
}
# --- 3. 実行と結果のグラフ化 ---
power_results <- data.frame(
n_per_group = n_list,
power = sapply(n_list, get_power)
)
ggplot(power_results, aes(x = n_per_group, y = power)) +
geom_line(linewidth = 1) + geom_point(size = 3, color = "red") +
geom_hline(yintercept = 0.8, linetype = "dashed", color = "blue") +
scale_y_continuous(limits = c(0, 1), breaks = seq(0, 1, 0.1)) +
labs(title = "パワーカーブ: CLMM交互作用の検定力",
x = "サンプルサイズ(1群あたり)", y = "検定力 (Power)") +
theme_minimal()
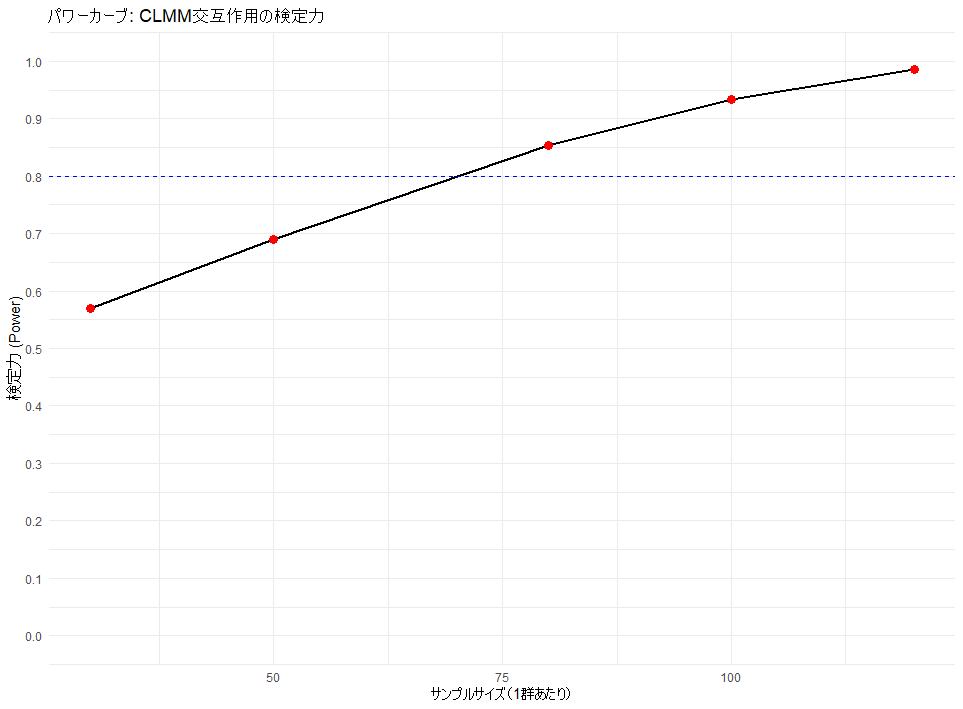
パワーカーブの解釈
シミュレーション結果をグラフ化することで、視覚的に必要人数を判断できる。
- 目標値: 一般的に、検定力(Power)が0.8(80%)を超えるポイントを最小必要人数とする(上記の場合 70 例あたりで 80 %を超え、80 例あればまず間違いなく 80 %を超えると考えられる)。
- 傾向: 人数を増やすほど検定力は上がるが、ある一点を超えると伸びが鈍化する。コストと精度のバランスが良い点を見極める必要がある。
- 安定性: 試行回数が少ないとグラフがガタつく。最終判断には必ず1000回の試行を行い、曲線を安定させるべきである。
実践する際のガイド・注意点
- 脱落率(ドロップアウト)を考慮する:シミュレーションで得られる数値は、解析に回せる完遂者の人数である。20%の脱落が見込まれるなら、必要人数を0.8で割った数を目標にリクルートすべきである(80 例であれば、80 / 0.8 = 100)。
- 試行回数のステップアップ:コードの修正中は100回程度の少ない試行回数で動作を確認し、最終的に1000回で回すのが効率的である。
- パラメータの根拠:「改善効果」や「個人差」の数値は、先行研究やパイロットデータを参考に設定することで、結果の説得力が増す。
まとめ
GLMM(順序ロジスティック)のサンプルサイズ計算は一見難解だが、Rでのシミュレーションという武器を持てば恐れることはない。1000回の試行に基づいたパワーカーブは、研究計画に揺るぎない根拠を与えてくれるはずである。







コメント