メタアナリシスのために信頼区間から標準誤差を逆算する方法

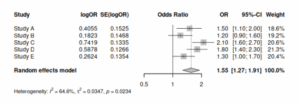
メタアナリシスをしたい場合、統合する点推定値と標準誤差が必要になる。

曝露有り無しと疾患ありなしが生データとして入手できる場合は問題ないが、多変量調整のあとの点推定値と95%信頼区間しかない場合は多い。

点推定値＋95%信頼区間しか手に入らない場合、どうやって標準誤差を推定するか。

信頼区間はどのように計算されているか？

95%信頼区間がどのように構成されているかを考えればいい。

95%信頼区間の構成から逆算すれば標準誤差が求まる。

95%信頼区間は、

$$ 推定値 \pm 1.96 \times 標準誤差 $$

で計算されている。

1.96は、標準正規分布において95%を表すクォンタイルだ。

統合するのは、オッズ比やハザード比のことが多い。

オッズ比もしくはハザード比をR、標準誤差をSEとすると、

95%信頼区間は、

$$ \exp(\log(R) \pm 1.96 SE) $$

で計算されている。

t 分布で推定している場合は、t 分布のクォンタイルを使う必要がある。

その場合は、1.96 よりも少し大きくなる。

信頼区間から標準誤差を計算するにはどうすればいいか？

95%信頼区間の上限をUL、下限をLLとすると、以下のように標準誤差が計算できる。

\begin{array}{lcl} \displaystyle
\displaystyle \frac{\log(UL) – \log(LL)}{2 \times 1.96} \\
\displaystyle = \frac{(\log(R) + 1.96 SE) – (\log(R) – 1.96 SE)}{2 \times 1.96} \\
\displaystyle = \frac{2 \times 1.96 SE}{2 \times 1.96} \\
= SE
\end{array}

例えば、ハザード比が2.1、95%信頼区間が1.6から2.7だとすると、標準誤差は

\begin{array}{lcl} \displaystyle
\frac{\log(2.7) – \log(1.6)}{2 \times 1.96} \\
\displaystyle = \frac{0.9932518 – 0.4700036}{2 \times 1.96} \\
= 0.1334817
\end{array}

と計算される。

まとめ

標準誤差を多変量調整済み相対リスクの95%信頼区間から求めれば、観察型研究の場合でも、交絡の影響を適切にコントロールした推定値の統合が可能になる。

観察型研究の結果を統合したい場合は、多変量調整済みの推定値から、標準誤差を逆算する方法を使うのがよい。

ハザード比やオッズ比など相対リスクの標準誤差を信頼区間から逆算する【エクセル計算機】

エクセルファイルを作成した。

よければどうぞ。

ハザード比やオッズ比など相対リスクの標準誤差を信頼区間から逆算する【エクセル計算機】 | TKER SHOP

使い方解説動画。

こちらもよければどうぞ。

おすすめ書籍

新版 メタ・アナリシス入門