R で制限付き最尤推定量 REML でオッズ比を統合するメタアナリシス

オッズ比を制限付き最尤推定量 REML で統合する方法の解説。

R で実行する。

制限付き最尤推定量でオッズ比を統合する意味

オッズ比のメタアナリシスをするときに、対数を取るのは正規分布に近似した分布にしたいからだ。

漸近的正規近似と呼ぶ。

漸近的正規近似の条件では、制限付き最尤推定量 Restricted Maximum Likelihood (REML) estimator が理論的に自然で性質がいい。

より柔軟な変量モデル。

オッズ比のメタアナリシスをするにはこの方法が最も適切。

反復計算が含まれていて、複雑なために、簡便な方法 DerSimonian-Laird の方法がとられていた。

DerSimonian-Laird の方法は、以下を参照。

コンピューターが簡単に使える今や、反復計算は難しくなくなった。

制限付き最尤推定量の統合オッズ比を求めるには？

使用するデータは以下の通り。

a <- c(3,7,5,102,28,4,98,60,25,138,64,45,9,57,25,65,17)
n1 <- c(38,114,69,1533,355,59,945,632,278,1916,873,263,291,858,154,1195,298)
c <- c(3,14,11,127,27,6,152,48,37,188,52,47,16,45,31,62,34)
n0 <- c(39,116,93,1520,365,52,939,471,282,1921,583,266,293,883,147,1200,309)
dat <- data.frame(a,n1,c,n0)

まず個々の研究のオッズ比と標準誤差を計算する。

ai <- dat$a
bi <- dat$n1 - dat$a
ci <- dat$c
di <- dat$n0 - dat$c
tn <- dat$n1 + dat$n0
lgor <- log(ai*di/bi/ci)
se <- sqrt(1/ai+1/bi+1/ci+1/di)
low <- exp(lgor-1.96*se)
upp <- exp(lgor+1.96*se)
round(cbind(ORi=exp(lgor), LLi=low, ULi=upp),4)

固定効果モデルの漸近分散法で統合してみる。

均質性の検定Q1と有意性の検定Q2を行う。

k <- length(ai)
# --------------- fixed effects ---------------
w <- 1/se/se
sw <- sum(w)
varor <- exp(sum(lgor*w)/sw)
varorl <- exp(log(varor)-1.96*sqrt(1/sw))
varoru <- exp(log(varor)+1.96*sqrt(1/sw))
q1 <- sum(w*(lgor-log(varor))^2)
df1 <- k-1
pval1 <- 1-pchisq(q1, df1)
q2 <- log(varor)^2*sw
df2 <- 1
pval2 <- 1-pchisq(q2, df2)

変量効果モデルDerSimonian-Lairdの方法でも統合してみる。

# ------------- random-effects ----------------
tau2 <- (q1-(k-1))/(sw-sum(w*w)/sw)
tau2 <- max(0, tau2)
wx <- 1/(tau2+se*se)
swx <- sum(wx)
varord <- exp(sum(lgor*wx)/swx)
varordl <- exp(log(varord)-1.96*sqrt(1/swx))
varordu <- exp(log(varord)+1.96*sqrt(1/swx))
qx2 <- log(varord)^2*swx
dfx2 <- 1
pvalx2 <- 1-pchisq(qx2, dfx2)

制限付き最尤推定量REML estimatorを計算する。

DerSimonian-Lairdの方法で計算された $ \hat{\tau}^2 $ を初期値にする。

# ----------- REML method -----------
intau <- tau2
tau <- intau
nrep <- 10
newt <- 1:nrep
for (i in 1:nrep){
wb <- 1/(tau+se*se)
ormb <- exp(sum(lgor*wb)/sum(wb))
qf <- k/(k-1)*(lgor-log(ormb))^2-se*se
dkx <- (-1*sum(lgor*wb*wb)+log(ormb)*sum(wb*wb))/sum(wb)
qf2 <- -2*k/(k-1)*(lgor-log(ormb))*dkx
h <- sum(wb*wb*(qf-tau))
dh <- sum(-2*wb*wb*wb*(qf-tau)+wb*wb*(qf2-1))
newt[i] <- tau-h/dh
rel <- abs((newt[i]-tau)/tau)
tau <- newt[i]
}

$ \hat{\tau}^2 $ が4回目の反復計算で収束しているのがわかる。

> newt
[1] 0.02115981 0.02206697 0.02209898 0.02209902 0.02209902 0.02209902 0.02209902
[8] 0.02209902 0.02209902 0.02209902

反復計算で推定された $ \hat{\tau}^2 $ を用いて統合オッズ比を計算する。

wg <- 1/(tau+se*se)
swg <- sum(wg)
orRM <- exp(sum(lgor*wg)/swg)
orRMl <- exp(log(orRM)-1.96*sqrt(1/swg))
orRMu <- exp(log(orRM)+1.96*sqrt(1/swg))
qx2RM <- log(orRM)^2*swg
pvalx2RM <- 1-pchisq(qx2RM, dfx2)

統合した結果3つを比較してみる。

#----- Fixed Effect Variance-based -----
list(round(c(ORv=varor, LL=varorl, UL=varoru, Q1=q1, df1=df1,
P1=pval1, Q2=q2, df2=df2, P2=pval2),4))
#----- Random Effect DerSimonian-Laird -----
list(round(c(ORdl=varord, LL=varordl, UL=varordu, Q2dl=qx2,
df2dl=dfx2, P2dl=pvalx2, tau2=tau2),4))
#----- Restricted Maximum Likelihood -----
list(round(c(ORrm=orRM, LL=orRMl, UL=orRMu, Q2rm=qx2RM,
df2rm=dfx2, P2rm=pvalx2RM, tau2=tau), 4))

統合オッズ比の推定値はどれも似通っているが、制限付き最尤推定量は95%信頼区間が若干広くなっている。

> #----- Fixed Effect Variance-based -----
> list(round(c(ORv=varor, LL=varorl, UL=varoru, Q1=q1, df1=df1,
+ P1=pval1, Q2=q2, df2=df2, P2=pval2),4))
1
   ORv      LL      UL      Q1     df1      P1      Q2     df2      P2
0.7831  0.7067  0.8677 21.4798 16.0000  0.1608 21.8063  1.0000  0.0000
>
> #----- Random Effect DerSimonian-Laird -----
> list(round(c(ORdl=varord, LL=varordl, UL=varordu, Q2dl=qx2,
+ df2dl=dfx2, P2dl=pvalx2, tau2=tau2),4))
1
  ORdl      LL      UL    Q2dl   df2dl    P2dl    tau2
0.7908  0.6949  0.8998 12.6794  1.0000  0.0004  0.0169
>
> #----- Restricted Maximum Likelihood -----
> list(round(c(ORrm=orRM, LL=orRMl, UL=orRMu, Q2rm=qx2RM,
+ df2rm=dfx2, P2rm=pvalx2RM, tau2=tau), 4))
1
  ORrm      LL      UL    Q2rm   df2rm    P2rm    tau2
0.7910  0.6906  0.9060 11.4700  1.0000  0.0007  0.0221

個々の研究と統合オッズ比のフォレストプロットを描く

個々の研究のグラフを描いて、統合オッズ比と95%信頼区間を描く。

漸近分散法、DerSimonian-Lairdの方法、制限付き最尤推定量の3つ。

# ------------- individual graph ----------------
id <- k:1
plot(exp(lgor), id, ylim=c(-4,20),
log="x", xlim=c(0.1,10), yaxt="n", pch="",
ylab="Citation", xlab="Odds ratio")
title(main=" Variance-based method ")
symbols(exp(lgor), id, squares=sqrt(tn),
add=TRUE, inches=0.25)
for (i in 1:k){
j <- k-i+1
x <- c(low[i], upp[i])
y <- c(j, j)
lines(x, y, type="l")
text(0.1, i, j)
}
# -------------- Combined graph --------------
varorx <- c(varorl, varoru)
varory <- c(-1, -1)
lines(varorx, varory, type="o", lty=1, lwd=2)
varordx <- c(varordl, varordu)
varordy <- c(-2, -2)
lines(varordx, varordy, type="o", lty=1, lwd=2)
abline(v=c(varor, varord), lty=2)
abline(v=1)
text(0.2, -1, "Combined:fixed")
text(0.2, -2, "Combined:random")
orRMx <- c(orRMl, orRMu)
orRMy <- c(-3, -3)
lines(orRMx, orRMy, type="o", lty=1, lwd=2)
abline(v=c(varor, varord, orRM), lty=2)
text(0.2, -3, "Combined:REML")

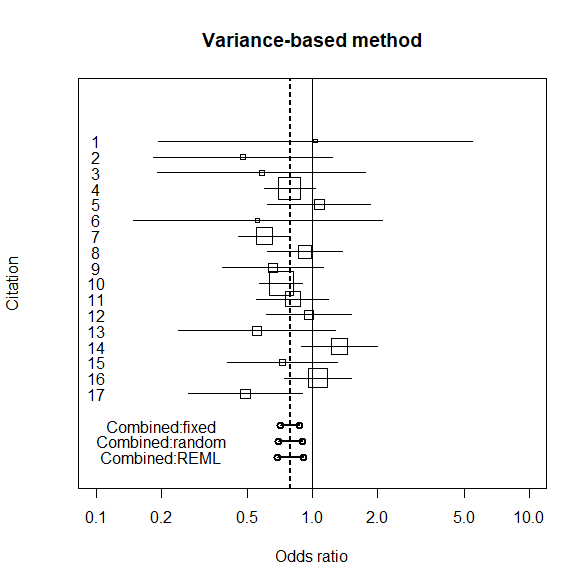
metaforパッケージを使うとどうなるか？

metaforパッケージを使ってREMLをやってみる。

escalc()で推定値 esitimateと分散 varianceを計算する。

measureは指標とする数値。今回はオッズ比。

yiは推定値、viは分散。

rma.uni()で、method=”REML”で制限付き最尤推定量の計算になる。

library(metafor)
dat.escalc <- escalc(measure="OR", ai=a, n1i=n1, ci=c, n2i=n0, data=dat)
res.reml <- rma.uni(yi, vi, method="REML", data=dat.escalc, control=list(verbose=T, tau2.init=tau2))
summary(res.reml)
round(exp(c(ORrm=res.reml$b, LLrm=res.reml$ci.lb, ULrm=res.reml$ci.ub)),4)

推定結果はこちら。

> res.reml <- rma.uni(yi, vi, method="REML", data=dat.escalc, control=list(verbose=T, tau2.init=tau2))
Iteration 0     tau^2 = 0.0169
Iteration 1     tau^2 = 0.0235
Iteration 2     tau^2 = 0.0237
Iteration 3     tau^2 = 0.0237
Fisher scoring algorithm converged after 3 iterations.
>
> summary(res.reml)
Random-Effects Model (k = 17; tau^2 estimator: REML)
logLik  deviance       AIC       BIC      AICc
-4.3260    8.6519   12.6519   14.1971   13.5750
tau^2 (estimated amount of total heterogeneity): 0.0237 (SE = 0.0257)
tau (square root of estimated tau^2 value):      0.1540
I^2 (total heterogeneity / total variability):   32.51%
H^2 (total variability / sampling variability):  1.48
Test for Heterogeneity:
Q(df = 16) = 21.4798, p-val = 0.1608
Model Results:
estimate      se     zval    pval    ci.lb    ci.ub
-0.2345  0.0702  -3.3404  0.0008  -0.3720  -0.0969  ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
>
> round(exp(c(ORrm=res.reml$b, LLrm=res.reml$ci.lb, ULrm=res.reml$ci.ub)),4)
ORrm   LLrm   ULrm
0.7910 0.6893 0.9077

参考書籍 メタ・アナリシス入門の結果と信頼区間の上限下限が若干異なった。

$ \hat{\tau}^2 $ の初期値を合わせてみたが、解決しなかった。

ほんの少しの違いなので、問題にすることはないと考える。

metafor パッケージを使用した結果を使えばよいと思う。

また、フォレストプロットはこちら。

forest(res.reml)

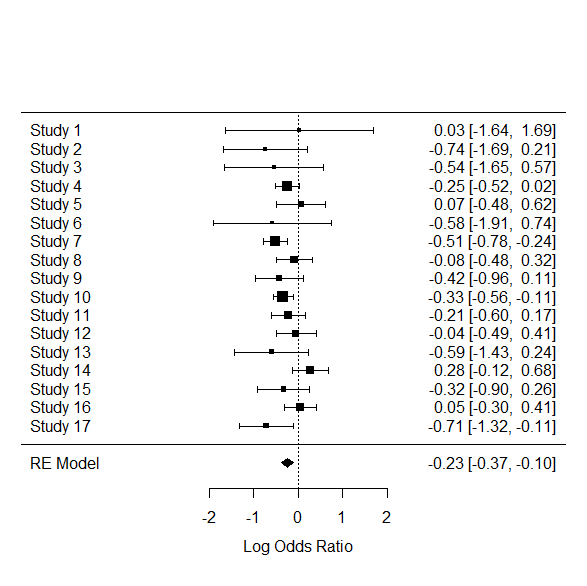
まとめ

より柔軟な変量モデル、制限付き最尤推定量（REML）を R で実行する方法を解説した。

metafor パッケージを使って計算するのが良い。

参考になれば。

参考書籍

丹後俊郎著　メタ・アナリシス入門　朝倉書店
5.1 より柔軟な変量モデル―制限付き最尤推定量
5.3.1 βブロッカーの臨床試験―オッズ比
付録B.10 varorRM.s: varor.s + REML for odds ratio

新版はこちら