マンホイットニーの U 検定に最低限必要なサンプル数はいくつか

マンホイットニーのU検定を行う際に最低限何例あればよいか？

マンホイットニーのU検定はどんな計算をしているか？

マンホイットニーのU検定はそもそもどんな計算をしているか、という点から、各群最低何例必要かを考えたい。

数学的には同値になる、方法が2つある。

方法 1

方法１は、数字の大小で大きい場合は１，小さい場合は０、同じ場合は1/2とスコアを付けて合計して、検定統計量を計算する方法だ。

例えば、群ｘの1.04の場合、群ｙの1.15, 0.88, 0.90, 0.74, 1.21と比較すると、0（小さい）、１（大きい）、１、１、０というふうにスコアがつけられる。

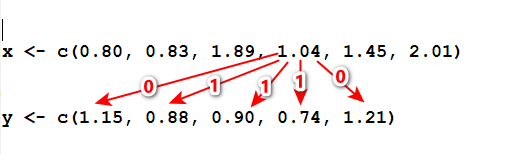
これをすべての値について、スコアを付けて合計する。

以下のＲスクリプトでMethod Oneと書いてあるところが、スコアを合計しているところである。

Ux1、Uy1がMethod Oneで計算した結果である。

# wilcoxon rank sum test and mann-whitney U test
x <- c(0.80, 0.83, 1.89, 1.04, 1.45, 2.01)
y <- c(1.15, 0.88, 0.90, 0.74, 1.21)
wilcox.test(x, y)

#Method One:
Ux1 <- sum(
c(0,0,0,1,0),
c(0,0,0,1,0),
c(1,1,1,1,1),
c(0,1,1,1,0),
c(1,1,1,1,1),
c(1,1,1,1,1)
)
Uy1 <- sum(
c(1,1,0,1,0,0),
c(1,1,0,0,0,0),
c(1,1,0,0,0,0),
c(0,0,0,0,0,0),
c(1,1,0,1,0,0)
)

#Method Two:
x.rank <- c(2,3,10,6,9,11)
y.rank <- c(7,4,5,1,8)
Rx <- sum(x.rank)
Ry <- sum(y.rank)
nx <- length(x)
ny <- length(y)
Ux2 <- Rx-nx*(nx+1)/2
Uy2 <- Ry-ny*(ny+1)/2

方法 2

方法２（Method Two）は、両群の値を小さい順に並べて、通しで順位をつけて、群ごとに合計する。

ともに群ごとに１からサンプルサイズ（今回は６と５）までの合計（nx*(nx+1)/2, ny*(ny+1)/2 のところ）を引くと、Ux2, Uy2になる。

結果として、Ux1, Ux2は同じ値になるし、Uy1, Uy2も同じ値になる。

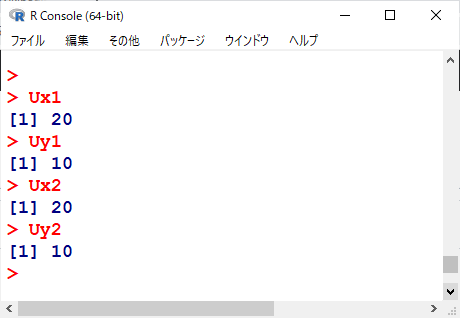
要するに、Method Oneの結果と、Method Twoの結果が一致しているのがわかる。

いずれの方法でも結果は同じということだが、つまりはマンホイットニーのU検定はこのような計算をして検定しているということである。

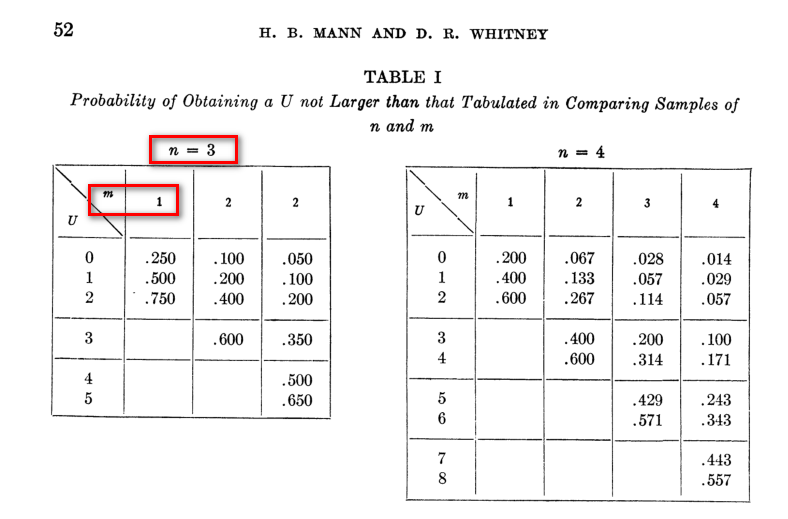
原著論文の数値表を確認すると、サンプルサイズが大きい群がn=6、小さい群がn=5なので、n=6の表を見ることになる。

m=5で、Uが10（上記ではUy1やUy2が10であった）を見ると .214 とある。

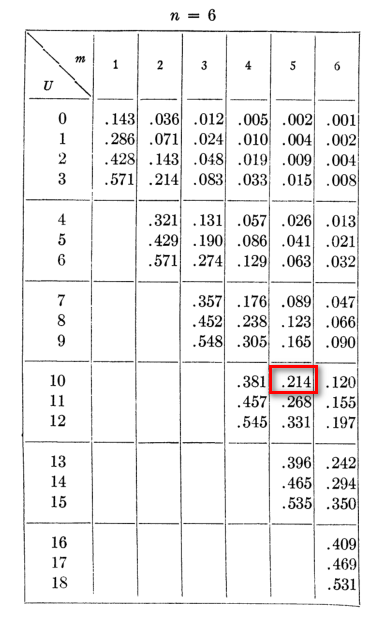
この確率は片側なので、通常の両側検定とするとその倍の 0.428 が求めるべき有意確率である。

R の関数の wilcox.test() で計算すると以下の通りとなり、ほぼ同じ有意確率 0.4286 が得られる。

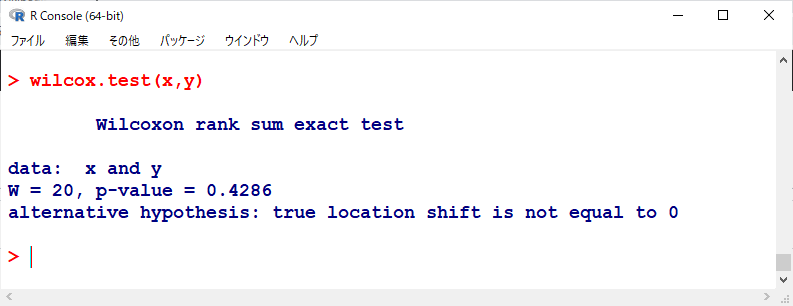
W=20が検定統計量であるが、Ux1, Ux2の20のほうを使っている。

小さいほうを使うのがもともとの方法であるが、R では、大きいほうを使って計算している。

マンホイットニーのU検定は各群最低何例必要か？

上記の通り、マンホイットニーのUは大きい場合は１、同じ場合は0.5を足し合わせていく、もしくは順位を足し合わせていくだけなので、極端な話 n=1 でも計算できる。

事実、マンホイットニーの原著論文を見ると、最小のサンプルサイズは、n=3, m=1、つまり、群１は３例、群２は１例という状況で検定統計量Uの有意確率を示している。

理論的には、3例と1例の合計4例で解析できるということである。

まとめ

マンホイットニーのU検定がどのような計算をしているのか、原著論文ではどのような想定をしていたのかを確認することで、最低限何例必要かを追求した。

最小のサンプルサイズとして、3例と1例の比較でも理論上は可能であることを確認した。

関連記事

サンプル数計算については、過去記事参照。

参考文献

マンホイットニーの原著論文

On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other