「実験で有意差が出たが、この差はどれくらい大きいと言えるのか?」
「論文で効果量を報告するように言われたが、計算方法がわからない」
統計解析において避けて通れないのが効果量(Effect Size)だ。特に、同一対象に繰り返し測定を行う「反復測定分散分析」では、偏イータ2乗(Partial Eta Squared)という指標が標準的に用いられる。
本記事では、統計初心者に向けて、偏イータ2乗の意味からRでの計算、そして信頼性の高いグラフ作成までを詳しく解説する。
反復測定分散分析とは
反復測定分散分析(Repeated Measures ANOVA)は、同一の対象に対して、条件を変えて複数回測定したデータを比較する手法である。
- 例: 学習アプリの効果を測るため、「使用前」「使用1ヶ月後」「使用3ヶ月後」のテストスコアを比較する。
この分析の最大の利点は、個人がもともと持っている能力差(個体間誤差)を計算から取り除ける点にある。これにより、条件による純粋な変化を検出しやすくなる(感度が高まる)。
効果量(偏イータ2乗)の必要性と目安
P値は「差があると言えるか(偶然ではないか)」を判定するが、サンプルサイズが大きければ微小な差でも有意になりやすい。一方、効果量はサンプルの数に左右されない「差の強さ」を表す。
反復測定分散分析で使われる偏イータ2乗($\eta_p^2$)は、「特定の要因が、他の要因を除いた全体の変動のうち、どの程度の割合を説明しているか」を示す指標である。
偏イータ2乗の計算式
$$\eta_p^2 = \frac{SS_{effect}}{SS_{effect} + SS_{error}}$$
判断の目安(Cohenの基準)
算出した値がどの程度のインパクトを持つかは、以下の基準を参考にするとよい。
| 効果の大きさ | 偏イータ2乗 ($\eta_p^2$) の値 |
| 小 (Small) | 0.01以上 |
| 中 (Medium) | 0.06以上 |
| 大 (Large) | 0.14以上 |
Rで実践:2群×3時点の混合デザイン
ここでは、実戦的な2群(介入群・対照群)×3時点(Pre・Mid・Post)の混合デザインを例に解析を行う。
解析スクリプト
# 必要なパッケージのロード
if (!require(afex)) install.packages("afex")
if (!require(effectsize)) install.packages("effectsize")
if (!require(emmeans)) install.packages("emmeans")
library(afex)
library(effectsize)
library(emmeans)
library(ggplot2)
# 1. サンプルデータの作成(20名が3回測定:ロング型)
set.seed(123)
dat_mixed <- data.frame(
ID = rep(1:20, each = 3),
Group = rep(c("A", "B"), each = 30),
Time = rep(c("Pre", "Mid", "Post"), 20),
Score = c(
rnorm(30, mean = c(50, 60, 70), sd = 5), # Group A: 上昇傾向
rnorm(30, mean = c(50, 52, 53), sd = 5) # Group B: 横ばい傾向
)
)
# 2. 混合デザインの分散分析
model_mixed <- aov_ez(id = "ID", dv = "Score", data = dat_mixed,
between = "Group", within = "Time")
# 3. 効果量(偏イータ2乗)の算出
res_mixed <- eta_squared(model_mixed, partial = TRUE)
# 結果の表示
print(model_mixed)
print(res_mixed)
結果出力
> # 結果の表示
> print(model_mixed)
Anova Table (Type 3 tests)
Response: Score
Effect df MSE F ges p.value
1 Group 1, 18 14.83 52.52 *** .404 <.001
2 Time 1.86, 33.44 26.37 28.14 *** .545 <.001
3 Group:Time 1.86, 33.44 26.37 13.42 *** .364 <.001
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘+’ 0.1 ‘ ’ 1
Sphericity correction method: GG
> print(res_mixed)
# Effect Size for ANOVA (Type III)
Parameter | Eta2 (partial) | 95% CI
------------------------------------------
Group | 0.74 | [0.54, 1.00]
Time | 0.61 | [0.43, 1.00]
Group:Time | 0.43 | [0.21, 1.00]
- One-sided CIs: upper bound fixed at [1.00].
> 実行結果の読み解きと解釈
解析の結果、以下のような極めて強い効果が示された。
効果量の解釈
| 要因 | 偏イータ2乗 ($\eta_p^2$) | 解釈 |
| Group (群間) | 0.74 | 最強の効果。 全体の変動の74%が群の違いに起因する。 |
| Time (時期) | 0.61 | 強い効果。 時期によるスコア変化が明確である。 |
| Group:Time (交互作用) | 0.43 | 最重要。 群によってスコアの推移が全く異なることを示す。 |
💡 交互作用($\eta_p^2 = 0.43$)の意義
今回の数値が高いことは、「A群は劇的に伸びたが、B群はほぼ変化しなかった」という、群と時間の相乗効果を科学的に裏付けている。
95%CIを用いた視覚化
モデルから計算される効果量を論じるのであれば、グラフのエラーバーもモデルから計算された95%信頼区間(CI)で揃えるのが適切である。
# モデルから推定平均値と95%CIを取得してグラフ化
plot_data_ci <- as.data.frame(emmeans(model_mixed, ~ Group * Time))
plot_data_ci$Time <- factor(plot_data_ci$Time, levels = c("Pre", "Mid", "Post"))
# 95%CIをエラーバーにしたグラフの描画
ggplot(plot_data_ci, aes(x = Time, y = emmean, color = Group, group = Group)) +
geom_line(size = 1.2) +
geom_point(size = 3) +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL), width = 0.1, size = 0.8) +
labs(title = "時期と群によるスコア推移(平均値 ± 95%CI)",
x = "測定時期", y = "推定平均値", color = "群") +
theme_minimal()
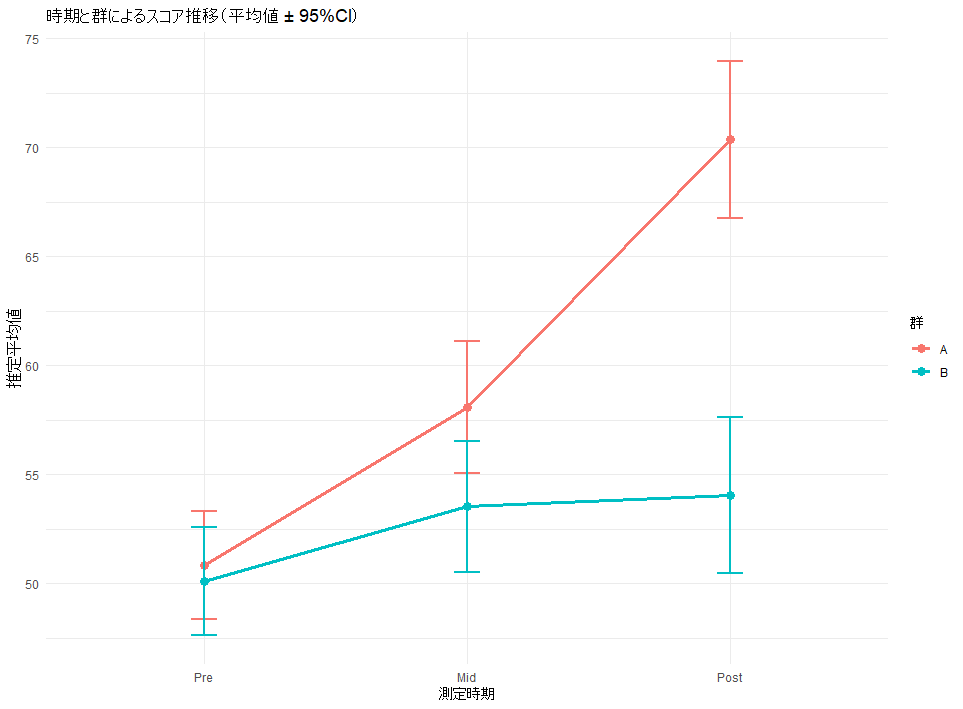
- なぜ95%CIか: 標準誤差(SE)よりも「平均値の推定の確かさ」を厳密に示せるからである。
実践にあたっての注意点
「ロング型」データの構造
Rの解析では、以下の「ロング型」形式が必須となる。ID = 1 の下に、ID = 2, 3 … の行が縦方向に積み重なる形式をロング型と呼ぶ。
| ID (参加者) | Time (時期) | Score (値) | Group |
| 1 | Pre | 50 | A |
| 1 | Mid | 55 | A |
| 1 | Post | 60 | A |
論文への記載例
「時期と群の交互作用を検討した結果、有意な差が認められた($F(1.86, 33.44) = 13.42, p < .001$)。効果量として偏イータ2乗を算出したところ、$\eta_p^2 = .43$ [95% CI: .21, 1.00] であり、大きな効果が認められた。」
まとめ
反復測定分散分析において、P値と効果量、そして信頼区間をセットで提示することは、現代の統計報告におけるスタンダードである。
- P値で「偶然ではないこと」を判定。
- 偏イータ2乗で「現象の影響力」を数値化。
- 95%CIグラフで「結果の頑健さ」を視覚化。
これらを揃えることで、解析結果の説得力は格段に向上する。本記事のスクリプトを参考に、ぜひ自身のデータでも算出を試みてほしい。
おすすめ書籍
誰も教えてくれなかった 医療統計の使い分け〜迷いやすい解析手法の選び方が,Rで実感しながらわかる!





コメント