メタアナリシスは、いくつかの研究で算出された数値を、適切に統合する方法。
一つ一つの研究では、検出力が不足していたものが、統合することで検出力を増し、統計学的に判断がつくようになる。
メタアナリシスの結果は、エビデンスレベルが高いと評価されている。
R でPetoの方法による統合オッズ比を求める方法。
Petoの方法によるメタアナリシスの計算例
データは以下の通り。
a <- c(3,7,5,102,28,4,98,60,25,138,64,45,9,57,25,65,17)
n1 <- c(38,114,69,1533,355,59,945,632,278,1916,873,263,291,858,154,1195,298)
c <- c(3,14,11,127,27,6,152,48,37,188,52,47,16,45,31,62,34)
n0 <- c(39,116,93,1520,365,52,939,471,282,1921,583,266,293,883,147,1200,309)
dat <- data.frame(a,n1,c,n0)
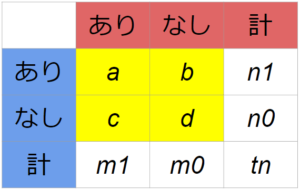
a, b, c, dは2×2の分割表のマス目の名前。
ai <- dat$a
bi <- dat$n1 - dat$a
ci <- dat$c
di <- dat$n0 - dat$c
表中のn1, n0, m1, m0, tnは周辺度数という。
周辺度数を計算する。
tn <- dat$n1 + dat$n0
n1 <- dat$n1
n0 <- dat$n0
m1 <- ai + ci
m0 <- bi + di
oが観察度数、
eが期待度数、
vが分散、
lgorは対数オッズ比、
seは標準誤差、
wは重み、
lowは95%信頼区間下限、
uppは95%信頼区間上限。
o <- ai
e <- n1*m1/tn
v <- (n1*n0/tn)*(m1*m0/tn)/(tn-1)
lgor <- (o-e)/v
se <- 1/sqrt(v)
w <- 1/se/se
low <- exp(lgor-1.96*se)
upp <- exp(lgor+1.96*se)
round(cbind("o-e"=o-e, v, lgor, low, upp),4)
計算結果を並べてみると、こうなる。
> round(cbind("o-e"=o-e, v, lgor, low, upp),4)
o-e v lgor low upp
[1,] 0.0390 1.4011 0.0278 0.1963 5.3853
[2,] -3.4087 4.7911 -0.7115 0.2005 1.2020
[3,] -1.8148 3.5477 -0.5115 0.2118 1.6973
[4,] -12.9876 52.9722 -0.2452 0.5978 1.0244
[5,] 0.8819 12.7149 0.0694 0.6186 1.8571
[6,] -1.3153 2.2863 -0.5753 0.1539 2.0564
[7,] -27.3981 54.2347 -0.5052 0.4624 0.7874
[8,] -1.8821 23.8590 -0.0789 0.6187 1.3804
[9,] -5.7786 13.8079 -0.4185 0.3883 1.1151
[10,] -24.7876 74.5949 -0.3323 0.5716 0.9000
[11,] -5.5522 25.6484 -0.2165 0.5469 1.1859
[12,] -0.7391 19.0354 -0.0388 0.6138 1.5074
[13,] -3.4572 5.9926 -0.5769 0.2522 1.2508
[14,] 6.7323 24.0149 0.2803 0.8873 1.9745
[15,] -3.6512 11.4271 -0.3195 0.4068 1.2973
[16,] 1.6326 30.0788 0.0543 0.7385 1.5093
[17,] -8.0379 11.6942 -0.6873 0.2835 0.8921
17の研究結果をPetoの方法で統合する。
swが重みの合計で、
petoが統合オッズ比、
petol, petouが95%信頼区間下限と上限。
q1は均質性の検定統計量。
q2が有意性の検定統計量。
# --------------- fixed effects ---------------
k <- length(ai)
sw <- sum(w)
peto <- exp(sum(lgor*w)/sw)
petol <- exp(log(peto)-1.96*sqrt(1/sw))
petou <- exp(log(peto)+1.96*sqrt(1/sw))
q1 <- sum(w*(lgor-log(peto))^2)
df1 <- k-1
pval1 <- 1-pchisq(q1, df1)
q2 <- (abs(sum(o-e))-0.5)^2/sum(v)
df2 <- 1
pval2 <- 1-pchisq(q2, df2)
list(round(c(ORp=peto, LL=petol, UL=petou, Q1=q1, df1=df1,P1=pval1, Q2=q2, df2=df2, P2=pval2),4))
結果をリストアップすると、こうなる。
統合オッズ比と95%信頼区間は0.7819 (0.7064 – 0.8656)。
均質性の検定はp=0.1643で統計学的有意でない。
均質という帰無仮説が棄却されない。
つまり、均質と言ってもいい。
有意性の検定はp<0.0001で統計学的有意。
> list(round(c(ORp=peto, LL=petol, UL=petou, Q1=q1, df1=df1,P1=pval1, Q2=q2, df2=df2, P2=pval2),4))
1
ORp LL UL Q1 df1 P1 Q2 df2 P2
0.7819 0.7064 0.8656 21.3816 16.0000 0.1643 22.2667 1.0000 0.0000
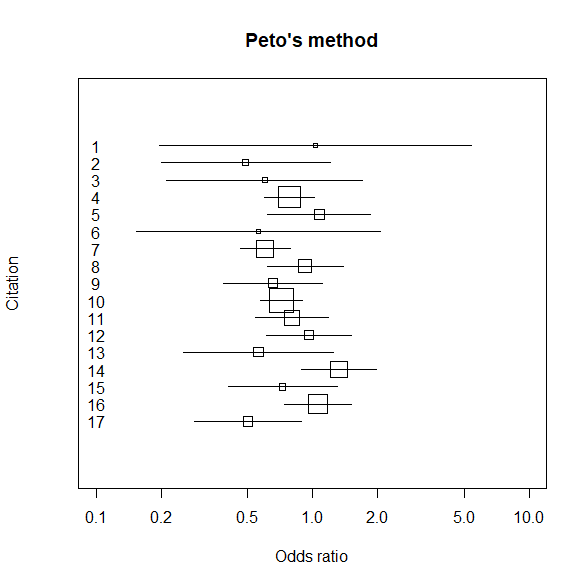
Petoの方法の結果を図示する
それぞれの研究結果を図示するスクリプト。
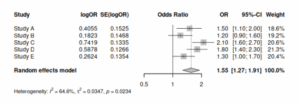
フォレストプロット Forest plotと呼ばれる。
X軸にオッズ比、
Y軸は研究ID。
一つの研究の重みは、四角の辺で表している。
辺はサンプルサイズの平方根。
最後に95%信頼区間下限から上限までラインを引く。
# ------------- individual graph ----------------
id <- k:1
plot(exp(lgor), id, ylim=c(-2,20),log="x", xlim=c(0.1,10), yaxt="n", pch="",ylab="Citation", xlab="Odds ratio")
title(main=" Peto's method ")
symbols(exp(lgor), id, squares=sqrt(tn),add=TRUE, inches=0.25)
for (i in 1:k){
j <- k-i+1
x <- c(low[i], upp[i])
y <- c(j, j)
lines(x, y, type="l")
text(0.1, i, j)
}
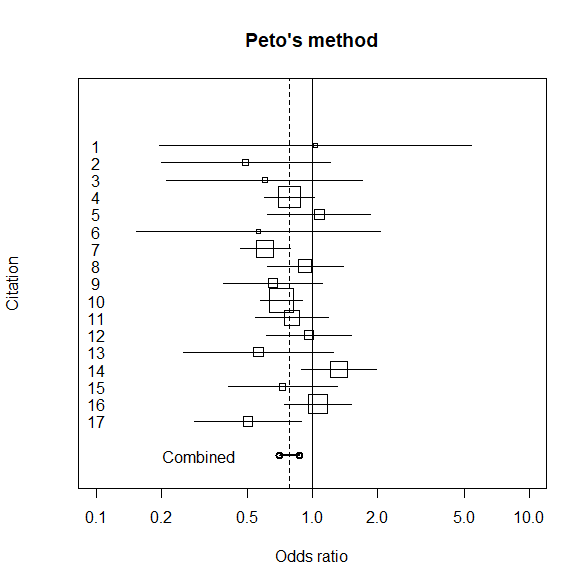
さらに統合オッズ比と95%信頼区間を図に追加する。
一番下にCombinedとあるのが、統合オッズ比と95%信頼区間。
# -------------- graph --------------
petox <- c(petol, petou)
petoy <- c(-1, -1)
lines(petox, petoy, type="o", lty=1, lwd=2)
abline(v=c(peto), lty=2)
abline(v=1)
text(0.3, -1, "Combined")
Petoの方法をパッケージを使って実行した場合
metaforパッケージのrma.peto()を使うと超楽々。
metaforパッケージは、最初の一回だけインストール。
install.packages("metafor")
rma.peto()内でa, b, c, dを指定するだけで、
あっという間に計算。
library(metafor)
rma.peto.res <- rma.peto(ai=a, bi=n1-a, ci=c, di=n0-c, data=dat)
rma.peto.res
計算結果は以下の通り。
均質性の検定結果は、Test for Heterogeneityの箇所を見る。
有意性の検定は、Model Results (log scale)のpvalを見る。
統合オッズ比と95%信頼区間は、Model Results (OR scale)を見る。
> rma.peto.res
Fixed-Effects Model (k = 17)
Test for Heterogeneity:
Q(df = 16) = 21.3816, p-val = 0.1643
Model Results (log scale):
estimate se zval pval ci.lb ci.ub
-0.2460 0.0518 -4.7447 <.0001 -0.3476 -0.1444
Model Results (OR scale):
estimate ci.lb ci.ub
0.7819 0.7064 0.8656
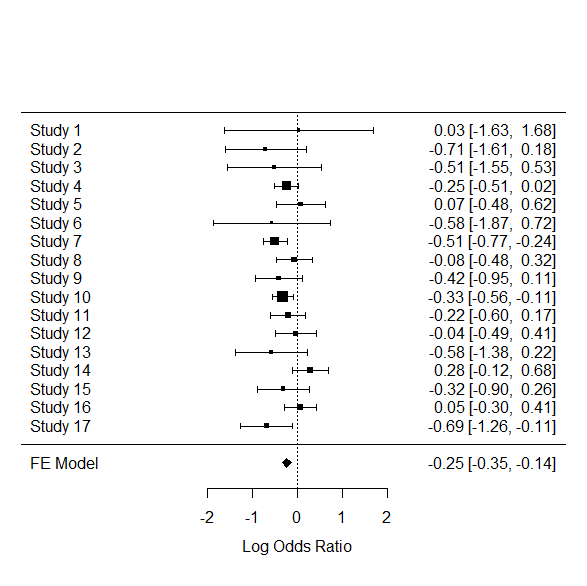
フォレストプロットも一瞬。
forest()だけでOK。
forest(rma.peto.res)
まとめ
オッズ比を Peto の方法で統合するメタアナリシスを R で行う方法を解説した。
参考になれば。
参考書籍
丹後俊郎著 メタ・アナリシス入門 朝倉書店
3.1 2×2分割表 3.1.1 Petoの方法―オッズ比
付録B.3 アルゴリズム3.1 peto.s

新版はこちら








コメント
コメント一覧 (3件)
[…] 個々の研究のサンプルサ… あわせて読みたい R でメタアナリシス―オッズ比をPetoの方法で統合する方法 […]
[…] R でメタアナリシス―オッズ比をPetoの方法で統合する方法 […]
[…] R でメタアナリシス―オッズ比をPetoの方法で統合する方法 […]