コホート研究のメタアナリシスは、複数の独立した研究結果を統合することで、より信頼性の高いエビデンスを導き出す強力な手法である。特に、調整オッズ比 (Adjusted Odds Ratio: AOR) や 調整ハザード比 (Adjusted Hazard Ratio: AHR) のような、交絡因子を調整した効果指標を統合する際には、その特性を理解し、適切な方法で解析を進めることが不可欠である。本記事では、コホート研究のメタアナリシスにおいて、AORやAHRを統合する際の一連の手順を、データの準備からRを用いた計算例まで、具体的に解説する。
データの準備方法
メタアナリシスを行うには、まず各研究から必要なデータを抽出して整理する必要がある。AORやAHRを統合する場合、以下の情報が各研究から抽出されているかを確認されたい。
- 調整オッズ比 (AOR) または調整ハザード比 (AHR): 各研究で報告されている値。
- 95%信頼区間 (95% CI) または標準誤差 (Standard Error: SE): AORまたはAHRに対応する信頼区間、もしくは直接SEが報告されている場合。SEが直接報告されていない場合は、信頼区間から計算が可能である。
- 研究ID/名称: 各研究を識別するための固有のIDや名称。
- 著者名、出版年など: 研究の特定に役立つ情報。
これらのデータは、通常スプレッドシート形式(例: CSV、Excel)で整理すると管理しやすくなる。
標準誤差の計算方法
多くの研究では、AORやAHR自体は報告されても、その標準誤差は直接報告されないことがある。その場合、95%信頼区間から標準誤差を逆算する必要がある。AORやAHRは対数変換することで正規分布に近似すると考えられるため、対数変換後の値とその標準誤差を使用する。
AORまたはAHRの95%信頼区間が [L,U] で与えられている場合、対数変換後の標準誤差 $ \text{SE}_{\text{log(OR or HR)}} $ は以下の式で計算できる。
$$ \text{SE}_{\text{log(OR or HR)}} = \frac{\log{U} − \log{L}}{2\times 1.96} $$
ここで、log は自然対数を表し、1.96 は95%信頼区間における標準正規分布のZ値である。
各研究から抽出したAORまたはAHRの対数変換値と、上記で算出した対数変換後の標準誤差をメタアナリシスに用いる。
統合方法
AORやAHRの統合には、主に固定効果モデル (Fixed-effect model) と 変量効果モデル (Random-effects model) の2つの方法がある。どちらのモデルを使用するかは、各研究間の異質性(heterogeneity)の有無や程度によって決定される。
- 固定効果モデル: 各研究で観察された効果は、単一の真の効果量の周りにばらついていると仮定する。研究間の異質性が低い場合に適している。一般的に、逆分散重み付け法が用いられ、各研究の重みは、その研究の精度の逆数(分散の逆数)に比例する。
- 変量効果モデル: 各研究で観察された効果は、異なる真の効果量を持つ母集団からランダムに抽出されたと仮定する。研究間の異質性が存在する、または異質性の存在が疑われる場合に推奨される。このモデルでは、研究内分散だけでなく、研究間分散(異質性の指標である$\tau^2$)も重みの計算に考慮される。多くのメタアナリシスでは、異質性が完全にないということは稀であるため、変量効果モデルが推奨されることが多い。
モデルを選択した後、統合された効果量(統合AORまたは統合AHR)とその信頼区間を算出する。
具体例と R 計算例
ここでは、Rのmetaパッケージを用いたAORまたはAHRのメタアナリシス例を示す。
まず、metaパッケージをインストールしてロードする。
# install.packages("meta")
library(meta)
次に、架空のデータフレームを作成する。ここでは、各研究の調整オッズ比(または調整ハザード比)とその95%信頼区間を仮定する。
# 架空のデータ作成
data_meta <- data.frame(
study = c("Study A", "Study B", "Study C", "Study D", "Study E"),
Ratio = c(1.5, 1.2, 2.1, 1.8, 1.3), # AORまたはAHRの値
lower = c(1.1, 0.9, 1.6, 1.4, 1.0),
upper = c(2.0, 1.6, 2.7, 2.3, 1.7)
)
metagen関数を用いてメタアナリシスを実行する。ここでは、TEに対数変換したRatio、seTEに対数変換したRatioの標準誤差を指定する。また、sm="OR"やsm="HR"で効果指標の種類を指定する。
# 変量効果モデルを用いたメタアナリシス
# Ratio, lower, upperを直接指定することも可能
meta_result <- metagen(
TE = log(Ratio),
lower = log(lower),
upper = log(upper),
data = data_meta,
studlab = study,
sm = "OR", # 効果指標が調整オッズ比の場合(調整ハザード比の場合は "HR" を指定)
common = FALSE, # 固定効果モデルを適用しない(変量効果モデル)
random = TRUE # 変量効果モデルを適用する
)
# 結果の表示
print(meta_result)
# フォレストプロットの作成
forest(meta_result)
上記のコードを実行すると、統合されたAOR(またはAHR)と95%信頼区間、異質性の指標($I^2$、Q統計量など)が表示される。また、フォレストプロットによって各研究の結果と統合結果が視覚的に示される。
実行結果:
> # 結果の表示
> print(meta_result)
Number of studies: k = 5
OR 95%-CI z p-value
Random effects model 1.5550 [1.2685; 1.9062] 4.25 < 0.0001
Quantifying heterogeneity (with 95%-CIs):
tau^2 = 0.0347 [0.0003; 0.4189]; tau = 0.1863 [0.0163; 0.6472]
I^2 = 64.6% [7.0%; 86.5%]; H = 1.68 [1.04; 2.72]
Test of heterogeneity:
Q d.f. p-value
11.30 4 0.0234
Details of meta-analysis methods:
- Inverse variance method
- Restricted maximum-likelihood estimator for tau^2
- Q-Profile method for confidence interval of tau^2 and tau
- Calculation of I^2 based on Q
> フォレストプロット:
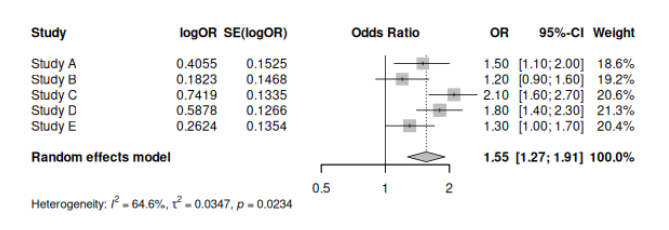
結果解釈
メタアナリシスの結果を解釈する際には、以下の点に注目する。
- 統合効果量: 統合されたAORまたはAHRの値自体が、曝露(または介入)がアウトカムに与える全体的な効果を示す。今回のデータでは 1.55
- 95%信頼区間: 統合効果量の信頼区間が1(AOR または AHRの場合)を跨いでいるかどうかを確認する。信頼区間が1を跨がない場合、統計的に有意な関連があると解釈される。上記の例では 1.27-1.91 で 1 をまたいでいない。
- 異質性: $ I^2 $ 統計量は、全ばらつきのうち異質性に起因する割合を示す。一般的に、$ I^2 $ が25%未満であれば異質性は低い、25%~50%であれば中程度、50%超であれば高いと判断される。異質性が高い場合は、その原因を探索するサブグループ解析やメタ回帰などの追加解析を検討する。上記の結果は、64.6 % で異質性は高いとの判断になる。
- フォレストプロット: 各研究の点推定値と信頼区間、そして統合された効果が視覚的に表示される。これにより、各研究のばらつきや統合結果との整合性を確認できる。
まとめ
コホート研究のメタアナリシスにおける調整オッズ比や調整ハザード比の統合は、複雑な手順を伴うが、適切なデータ準備と統計手法を用いることで、質の高いエビデンスを生成できる。特に、標準誤差の計算や変量効果モデルの選択は重要なポイントである。本記事で紹介したRを用いた計算例を参考に、ぜひご自身の研究に応用されたい。






コメント