相関係数を統合したい場合はどうやるか?
R での方法。
個々の研究の相関係数と95%信頼区間の準備
使うデータは以下の通り。
r が相関係数。
n がサンプルサイズ。
r <- c(0.307,-0.01,0.300,0.119,0.194,0.248)
n <- c(107,1524,154,6165,4138,1559)
z がFisherの分散安定化変換後の相関係数。
Hyperbolic arc-tangent 関数 atanh() を使うと簡単に変換できる。
z に変換した後の標準誤差は $ \sqrt{\frac{1}{n – 3}} $ になる。
zl, zu は z の95%信頼区間下限と上限。
rl, ru は zl, zuを逆変換した(元の世界に戻した)値。
z <- atanh(r)
se <- sqrt(1/(n-3))
Za <- qnorm(1-0.05/2)
zl <- z-Za*se
zu <- z+Za*se
rl <- (exp(2*zl)-1)/(exp(2*zl)+1)
ru <- (exp(2*zu)-1)/(exp(2*zu)+1)
Fisherの分散安定化変換の逆変換はtanh()
Hyperbolic arc-tangentの逆は、hyperbolic tangent。
なので、rl, ru の計算式はtanh()で置き換えられる。
以降はtanh()を使う。
以下のように、シンプルなスクリプトで書ける。
> (exp(2*zl)-1)/(exp(2*zl)+1)
[1] 0.12439197 -0.06018300 0.14890459 0.09431717 0.16450217 0.20082642
> tanh(zl)
[1] 0.12439197 -0.06018300 0.14890459 0.09431717 0.16450217 0.20082642
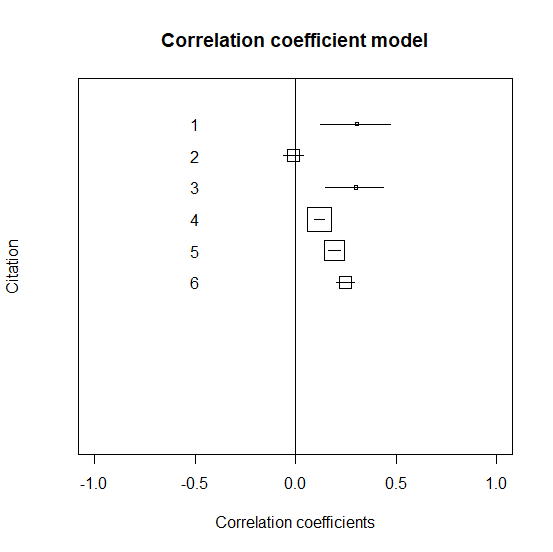
個々の研究の相関係数と95%信頼区間をグラフにする
個々の研究をグラフにするには以下の通り。
# ----- individual graph -----
k <- length(n)
id <- k:1
plot(r, id, ylim=c(-4, k+1), pch=" ", xlim=c(-1,1), yaxt="n",
ylab="Citation", xlab="Correlation coefficients")
title(" Correlation coefficient model ")
symbols(r, id, squares=sqrt(n-3), add=T, inches=0.25)
abline(v=0)
for (i in 1:k){
j <- k-i+1
x <- c(rl[i], ru[i])
y <- c(j, j)
lines(x, y, type="l")
text(-0.5, i, j)
}
グラフはこんな風に出力される。
固定効果で相関係数を統合する
$ w_i = n_i – 3 $ で重みづけ平均を取ると統合相関係数の推定値(Fisherの分散安定化変換後)。
tanh()で戻すと求める点推定値になる。
# ----- fixed effects -----
w <- n-3
sw <- sum(w)
varz <- sum(w*z)/sw
varr <- tanh(varz)
varrl <- tanh(varz-Za*sqrt(1/sw))
varru <- tanh(varz+Za*sqrt(1/sw))
q1 <- sum(w*(z-varz)^2)
df1 <- k-1
pval1 <- 1-pchisq(q1, df1)
q2 <- varz^2*sw
df2 <- 1
pval2 <- 1-pchisq(q2, df2)
変量効果で相関係数を統合する
Dersimonian-Lairdの方法の方法で統合する。
# ----- random effects -----
tau2 <- (q1-(k-1))/(sw-sum(w*w)/sw)
tau2 <- max(0, tau2)
wx <- 1/(tau2+se*se)
swx <- sum(wx)
varzd <- sum(wx*z)/swx
varrd <- tanh(varzd)
varrdl <- tanh(varzd-Za*sqrt(1/swx))
varrdu <- tanh(varzd+Za*sqrt(1/swx))
qx2 <- varzd^2*swx
pvalx2 <- 1-pchisq(qx2, df2)
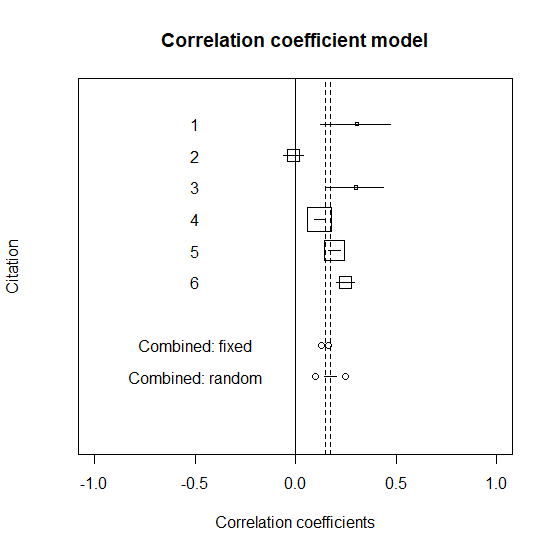
固定効果と変量効果の統合値をグラフに書き入れる
固定効果(グラフ中はCombined: fixed)と変量効果(グラフ中はCombined: random)をグラフに書き入れる。
# ----- graph -----
x <- c(varrl, varru)
y <- c(-1, -1)
lines(x, y, type="b")
x <- c(varrdl, varrdu)
y <- c(-2, -2)
lines(x, y, type="b")
abline(v=c(varr, varrd), lty=2)
text(-0.5, -1, "Combined: fixed")
text(-0.5, -2, "Combined: random")
グラフはこんな感じになる。
制限付き最尤推定量を用いた方法(REML)で相関係数を統合する
Restricted Maximum Likelihood estimator(REML)を適用した方法。
以下のスクリプトで繰り返し収束計算を行い解を求める。
$ \hat{\tau}^2 $ の初期値にはDerSimonian-Lairdの方法で求めた値を用いる。
# ----- REML method -----
intau <- tau2
tau <- intau
#
nrep <- 10
newt <- 1:nrep
for (i in 1:nrep){
wb <- 1/(tau+se*se)
zmb <- sum(wb*z)/sum(wb)
qf <- k/(k-1)*(z-zmb)^2-se*se
dkx <- (-1*sum(z*wb*wb)+zmb*sum(wb*wb))/sum(wb)
qf2 <- -2*k/(k-1)*(z-zmb)*dkx
h <- sum(wb*wb*(qf-tau))
dh <- sum(-2*wb*wb*wb*(qf-tau)+wb*wb*(qf2-1))
newt[i] <- tau - h/dh
rel <- abs((newt[i]-tau)/tau)
tau <- newt[i]
}
wg <- 1/(tau+se*se)
swg <- sum(wg)
zRM <- sum(z*wg)/swg
rRM <- tanh(zRM)
rRMl <- tanh(zRM-Za*sqrt(1/swg))
rRMu <- tanh(zRM+Za*sqrt(1/swg))
qx2RM <- zRM^2*swg
pvalx2RM <- 1-pchisq(qx2RM, df2)
tau2 <- tau
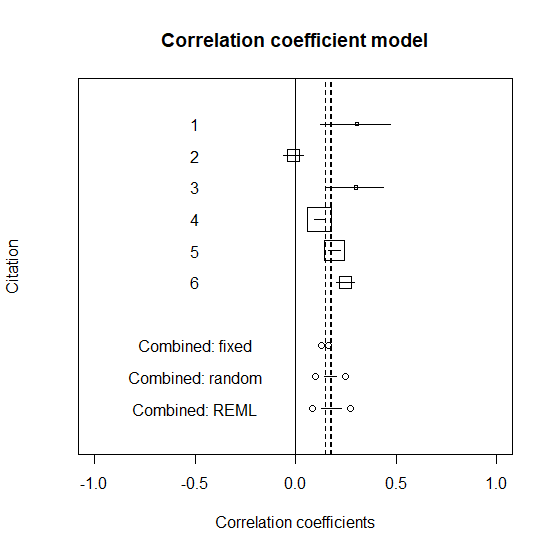
REMLの結果をグラフに書き入れる
# ----- REML graph -----
x <- c(rRMl, rRMu)
y <- c(-3, -3)
lines(x, y, type="b")
abline(v=rRM, lty=2)
text(-0.5, -3, "Combined: REML")
グラフはこちら。95%信頼区間は若干広くなるが、統計学的有意ではあった。
結果の数値を並べて比べてみる。
点推定値は固定効果→DerSimonian-Lairdの方法→REMLとだんだんに大きくなり、95%信頼区間もだんだん広くなっていった。
最終的に、統計学的有意($ P_{REML} = 0.0003 $)
> ## Fixed effects
> list(round(c(rFE=varr, LL=varrl, UL=varru, Q1=q1, df1=df1, p1=pval1, Q2=q2, df2=df2, p2=pval2),4))
[[1]]
rFE LL UL Q1 df1 p1 Q2 df2 p2
0.1463 0.1298 0.1627 76.8331 5.0000 0.0000 295.8090 1.0000 0.0000
>
> ## Random effects
> list(round(c(rDL=varrd, LL=varrdl, UL=varrdu, Q2DL=qx2, df2=df2, p2DL=pvalx2, "tau^2"=intau),4))
[[1]]
rDL LL UL Q2DL df2 p2DL tau^2
0.1741 0.0966 0.2496 19.0392 1.0000 0.0000 0.0078
>
> ## REML
> list(round(c(rRM=rRM, LL=rRMl, UL=rRMu, Q2RM=qx2RM, df2=df2, p2RM=pvalx2RM, "tau^2"=tau2),4))
[[1]]
rRM LL UL Q2RM df2 p2RM tau^2
0.1800 0.0831 0.2735 13.0604 1.0000 0.0003 0.0130
まとめ
相関係数の統合を R でやってみた。
相関係数にFisherの分散安定化変換をほどこして、n – 3 を重みにして重みづけ平均を取るのが中核だ。
相関係数が関心事の研究を統合するときにはこの方法が使える。
関連記事
漸近分散法によるオッズ比の統合
引用書籍
ネタ本はこちら
4.2 相関係数

新版はこちら









コメント