R で診断検査の感度・特異度を統合するメタアナリシス

2018年6月23日2024年10月14日

診断検査を統合する方法

感度・特異度のメタアナリシス

＞＞もう統計で悩むのは終わりにしませんか？

↑期間・数量限定で無料プレゼント中！

感度・特異度のメタアナリシスとは

診断検査の性能を見るのに、感度・特異度は欠かせない。

病気ありをきちんと診断できる割合が感度。

病気なしをきちんと病気なしと除外できる割合が特異度。

必要な数値は、検査陽性・陰性と、病気あり・なしをクロスさせた、２ｘ２表の各セルの人数だ。

いろいろな研究結果を統合するのがメタアナリシス。

感度・特異度の研究結果のメタアナリシスはどうやるか？

統合ROC曲線を描きたい場合はどうすればいいか？

複数の研究結果をプロットして可視化する

2×2の分割表の4つのマス目をa, b, c, dと表現することが多い。

	病気あり	病気なし
検査陽性	a	b
検査陰性	c	d

感度・特異度のメタアナリシスを行ってみるサンプルデータは、以下の通り。

a <- c(26,11,68,74+0.5,84,40,16,96,11,91,46,15,58,26)
b <- c(2,2,8,0+0.5,13,7,9,15,2,5,3,2,16,1)
c <- c(4,1,3,12+0.5,20,3,1,20,2,5,9,1,10,4)
d <- c(83,5,34,111+0.5,99,41,109,206,57,57,42,93,121,74)

感度は、病気ありの人のうち、検査が当たった人。

これが、検査陽性の割合。

病気ありの人が本当に病気ありと判断される割合が感度（Sensitivity, Se）。

特異度は、病気なしの人のうち、検査が陰性の人。

これが、検査陰性の割合。

病気なしの人が本当に病気なしと判断される割合が特異度（Specificity, Sp）。

これらを計算すると以下のとおりである。

Se <- a/(a+c)
Sp <- d/(b+d)
plot(1-Sp, Se, xlim=c(0,1), ylim=c(0,1))

図にすると以下のようになる。

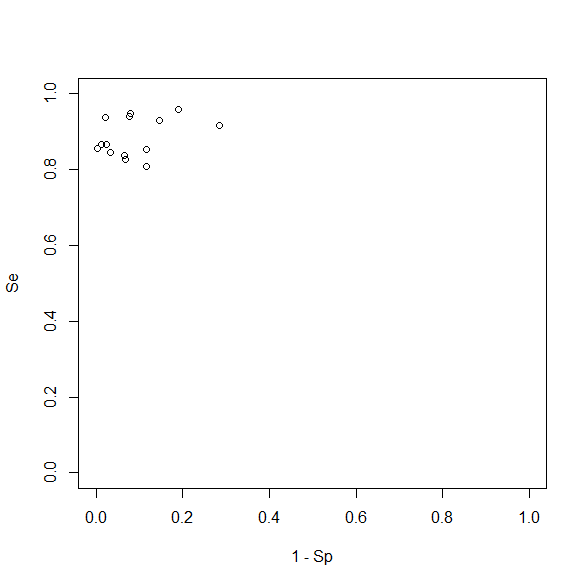
左上にかたまっているのが、各研究を表している点である。

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

感度と偽陽性から計算されるオッズ比を重みづけ線形回帰でチェックする

感度 Se と偽陽性 1-Sp のオッズ比（OR）を計算する。

これが診断のパワーの指標だ。

感度 Se と特異度 Sp のオッズ比（S）も計算する。

これはカットオフ値の影響を表す。

それぞれの試験結果の標準誤差 se を計算する。

標準誤差からそれぞれの試験の重み w を計算する。

OR と S の対数を使って、重み付け線形回帰分析を行う。

x <- 1-Sp
y <- Se
OR <- (y/(1-y))/(x/(1-x))
S <- (y/(1-y))/((1-x)/x)
se <- sqrt(1/a+1/b+1/c+1/d)
w <- 1/se/se
lm.res <- lm(log(OR) ~ log(S), weights=w)
summary(lm.res)

重み付け線形回帰分析の結果はこちら。

> summary(lm.res)
Call:
lm(formula = log(OR) ~ log(S), weights = w)
Weighted Residuals:
Min      1Q  Median      3Q     Max
-2.2693 -0.3663  0.7553  1.1976  1.8928
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)   4.2038     0.2566  16.383 1.41e-09 ***
log(S)       -0.2306     0.2336  -0.987    0.343
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.322 on 12 degrees of freedom
Multiple R-squared:  0.07509,   Adjusted R-squared:  -0.001985
F-statistic: 0.9742 on 1 and 12 DF,  p-value: 0.3431

結果は log(S) の係数は統計学的に有意でなく、OR は S の関数とは言えない。

つまり、カットオフ値の違いに影響はなく、診断オッズ比の統合が可能と判断できる。

プロットに回帰直線を乗せてチェックした図がこちら。

plot(log(S),log(OR),pch="",ylim=c(2,8))
symbols(log(S),log(OR),squares=w,add=TRUE)
abline(a=lm.res$coeff[1],b=lm.res$coeff[2])

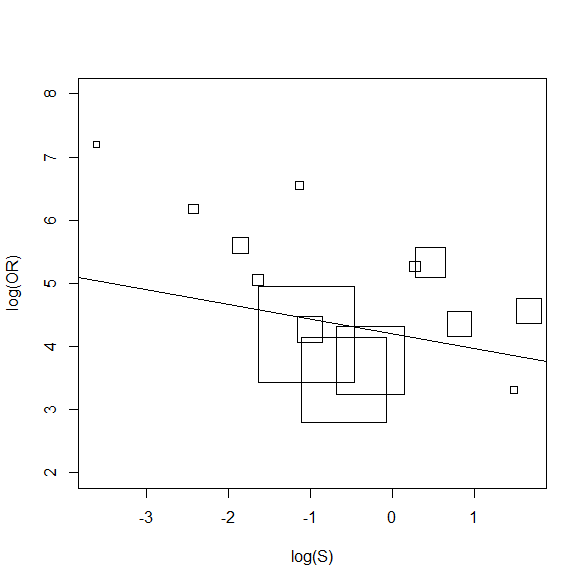
多少は傾いているが、傾きが 0 でないとは言えないという結果であった。

要約ROC曲線を書く

さまざまな感度・特異度分析研究の結果を要約した要約ROC曲線を描くにはどうしたらいいか？

線形回帰分析の結果を使って要約ROC曲線を描く。

alpha <- lm.res$coeff[1]
beta <- lm.res$coeff[2]
SROCC <- function(x,alpha=lm.res$coeff[1],beta=lm.res$coeff[2]){1/(1+exp(-1*alpha/(1-beta))*(x/(1-x))^(-1*(1+beta)/(1-beta)))}
plot(1-Sp, Se, xlim=c(0,1), ylim=c(0,1))
curve(SROCC, from=0, to=1, add=TRUE)

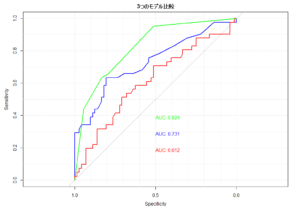
要約 ROC 曲線と各研究のプロットを重ねた図がこちら。

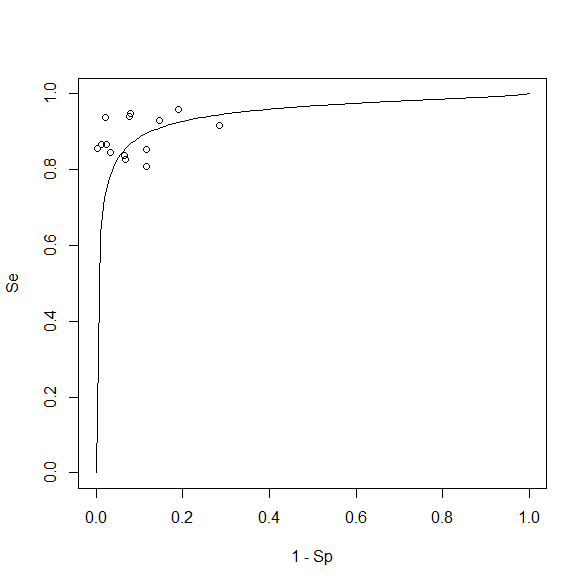
診断検査の統合オッズ比を計算する

統合オッズ比を計算するには、metaforパッケージを使う。

metaforパッケージを最初の一回だけインストールする。

install.packages("metafor")

metaforパッケージを呼び出し、統合オッズ比を計算する。

固定効果モデル、Mantel-Haenszelの方法、変量効果モデル（DerSimonian-Lairdの方法）で計算してみる。

library(metafor)
escalc1 <- escalc(measure="OR", ai=a, bi=b, ci=c, di=d)
rma.uni(yi, vi, method="FE", dat=escalc1)
rma.mh (ai=a, bi=b, ci=c, di=d)
rma.uni(yi, vi, method="DL", dat=escalc1)

まず、固定効果モデルの結果。

> rma.uni(yi, vi, method="FE", dat=escalc1)
Fixed-Effects Model (k = 14)
Test for Heterogeneity:
Q(df = 13) = 22.6789, p-val = 0.0457
Model Results:
estimate      se     zval    pval   ci.lb   ci.ub
4.3179  0.1733  24.9220  <.0001  3.9784  4.6575  ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’

Heterogeneityが統計学的に有意（ p-val = 0.0457 ）なので、変量効果モデルのほうが適切。

次に、Mantel-Haenszelの方法の結果。

> rma.mh (ai=a, bi=b, ci=c, di=d)
Fixed-Effects Model (k = 14)
Test for Heterogeneity:
Q(df = 13) = 22.9291, p-val = 0.0425
Model Results (log scale):
estimate      se     zval    pval   ci.lb   ci.ub
4.4046  0.1687  26.1014  <.0001  4.0738  4.7353
Model Results (OR scale):
estimate    ci.lb     ci.ub
81.8255  58.7827  113.9012
Cochran-Mantel-Haenszel Test:    CMH = 1180.3678, df = 1,  p-val < 0.0001
Tarone's Test for Heterogeneity: X^2 =   25.6687, df = 13, p-val = 0.0188

Heterogeneityはこちらも同様に有意（ p-val = 0.0425 ）

最後に、DerSimonian-Lairdの方法の結果。

固定効果モデルおよびMantel-Haenszelの方法で、Heterogeneityが統計学的有意だったので、DerSiminian-Lairdの方法が最も適切。

> rma.uni(yi, vi, method="DL", dat=escalc1)
Random-Effects Model (k = 14; tau^2 estimator: DL)
tau^2 (estimated amount of total heterogeneity): 0.3369 (SE = 0.3329)
tau (square root of estimated tau^2 value):      0.5804
I^2 (total heterogeneity / total variability):   42.68%
H^2 (total variability / sampling variability):  1.74
Test for Heterogeneity:
Q(df = 13) = 22.6789, p-val = 0.0457
Model Results:
estimate      se     zval    pval   ci.lb   ci.ub
4.5695  0.2565  17.8182  <.0001  4.0669  5.0722  ***
---
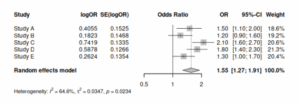
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1