割合のメタアナリシスの方法の解説
割合のメタアナリシスデータ準備
R で割合のメタアナリシスを行う準備
metafor と meta というパッケージをインストールして準備する
install.packages(c("metafor", "meta"))
library(metafor)
library(meta)
サンプルデータは、こちらのファイルを使う → MetaProp.RData
ダウンロードフォルダにダウンロードしたとして、以下のように書いて実行すると読み込める
xxxxx とある部分は、Windows の User 名の最初の 5 文字に変更する
load("C:/Users/xxxxx/Downloads/MetaProp.RData")
D
読み込まれたファイルはこちら
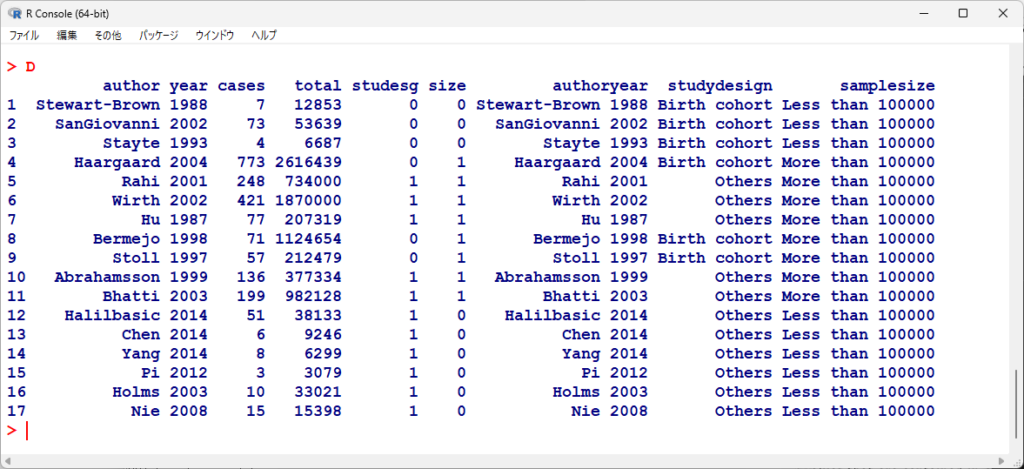
このデータセットの cases/total がそれぞれの試験のエンドポイントとしての割合となる
この割合を統合する方法である
メタアナリシスの方法 割合を統合する方法
割合は、0.5 付近の場合は、そのまま平均値をとっても大きな問題はないが、0.2 より小さかったり、0.8 より大きかったりすると問題が生じる
問題を回避するために、ロジット変換とダブルアークサイン変換が知られている
0.2 より小さいまたは 0.8 より大きい割合が中心となる場合は、ロジット変換がおすすめ
さらに、サンプルサイズが小さい、または、きわめて小さいまたは大きい割合になる場合は、ダブルアークサイン変換がおすすめとなる
今回のデータは、きわめて小さい割合になっているため、ダブルアークサイン変換を使う
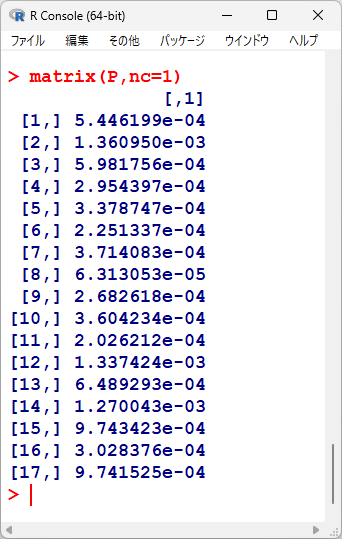
ここで、e-04, e-03 というのは、10 のマイナス 4 乗とか、3 乗とかという意味で、1 万分の 1 とか、1000 分の 1 とかという意味になり、とても小さい数値
ダブルアークサイン変換をして、統合の準備をするには、以下のように escalc() を使って、method=’PFT’ と指定する
xi に分子である cases, ni に分母である total を指定する
ies <- escalc(xi=cases, ni=total, data=D, measure='PFT')
そうすると、先ほどの D というデータセットの右端に yi と vi が追加される
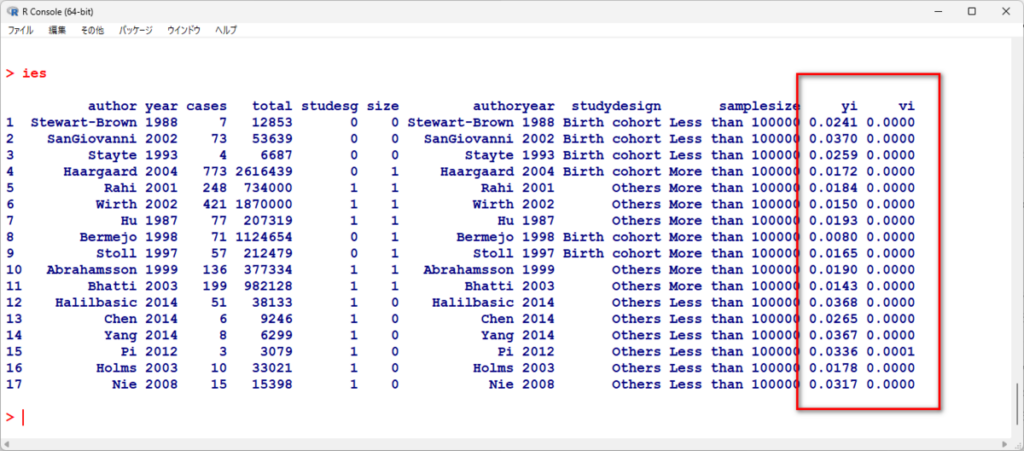
これが、各研究の割合のダブルアークサイン変換値と、その時の分散の値である
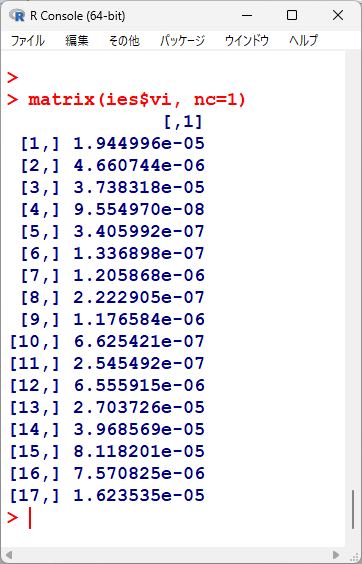
分散はとても小さいため、ほぼ全部 0.0000 としか見えていないが、もっと下の桁まで見れば、数値がある
次に、rma() 関数を使って、統合値を計算する
pes.da <- rma(yi, vi, data=ies)
計算した結果がこちら
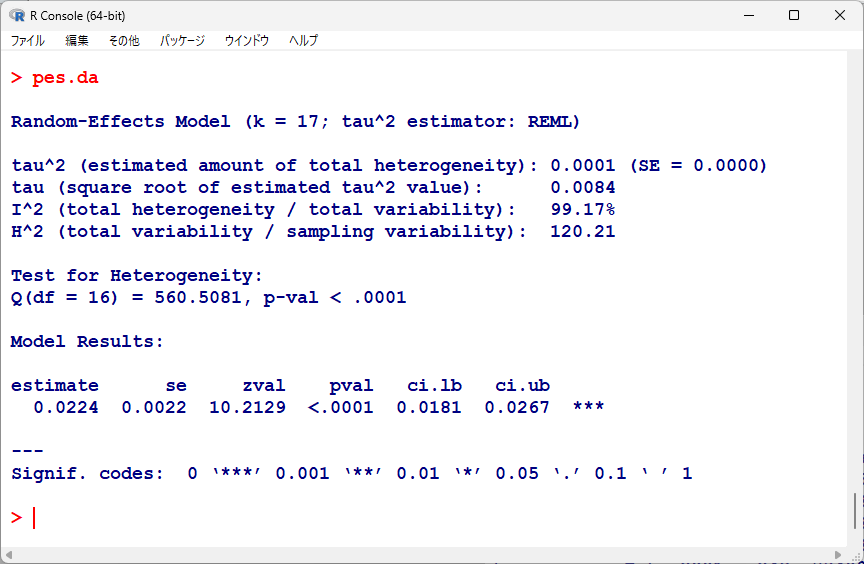
統合方法は、標準の方法で、REML が使われている
異質性があってもなくても、変量効果の方法 REML で統合しておけば、問題ない
統合値は、0.0224 と計算されている
この値は、ダブルアークサイン変換したままの値なので、predict() 関数を使って、元の割合に戻す
その方法は、以下の通り
pes <- predict(pes.da, transf=transf.ipft.hm, targs=list(ni=D$total))
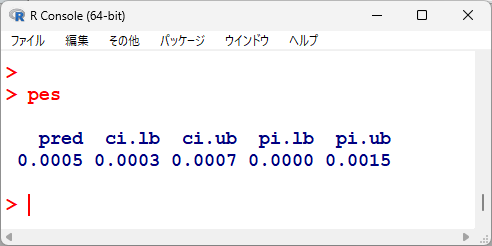
統合推定値は、0.0005 で、95 % 信頼区間は、ci.lb, ci.ub を見て、0.0003 から 0.0007 である
メタアナリシスの方法 割合の場合 フォレストプロット ファンネルプロット
メタアナリシスの結果の提示の仕方として、フォレストプロットが見やすい
フォレストプロットは meta パッケージを使うと、簡単できれいに書ける
まず、metaprop() 関数を使って、統合値の計算を行う
pes.summary <- metaprop(event=cases, n=total, studlab=authoryear, data=D, sm='PFT')
先ほどと同じくダブルアークサイン変換をする場合は、sm=’PFT’ という指定をする
変換なしの割合そのままの場合は ‘PRAW’, ロジット変換の場合は ‘PLO’ と指定する
event が分子で cases, n が分母で total, 各研究の名前は studlab で指定し authoryear とする
まず、分析結果は以下のようになる
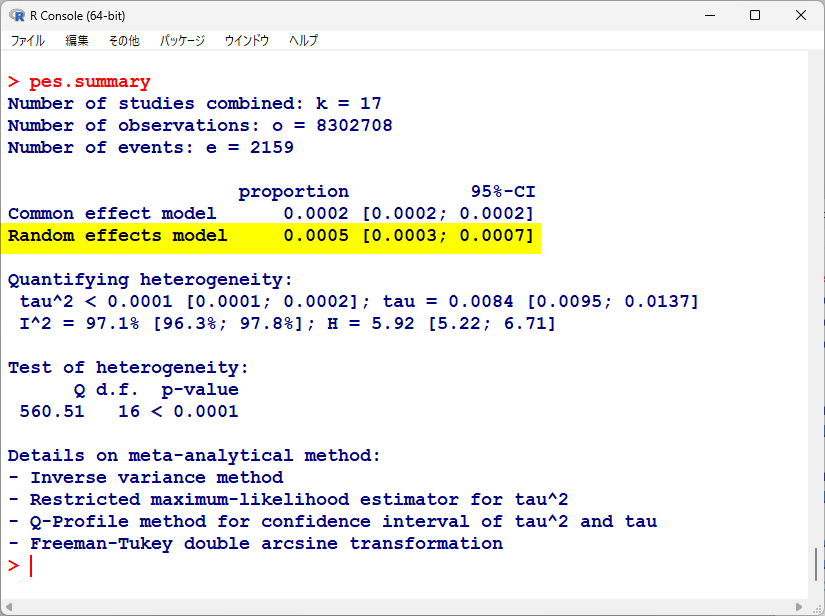
黄色ハイライト部分は、上記で計算した点推定値と区間推定上限下限と同じ値になっている
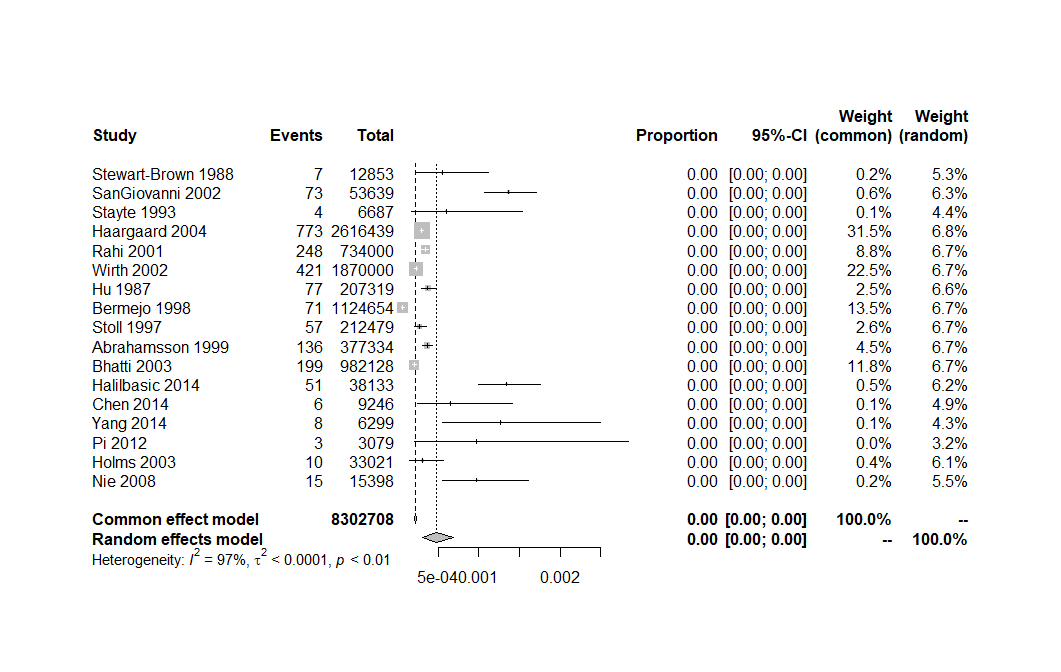
フォレストプロットを書くには、以下のように記述して実行する
forest(pes.summary)
そうすると、以下のようにきれいなフォレストプロットが書ける
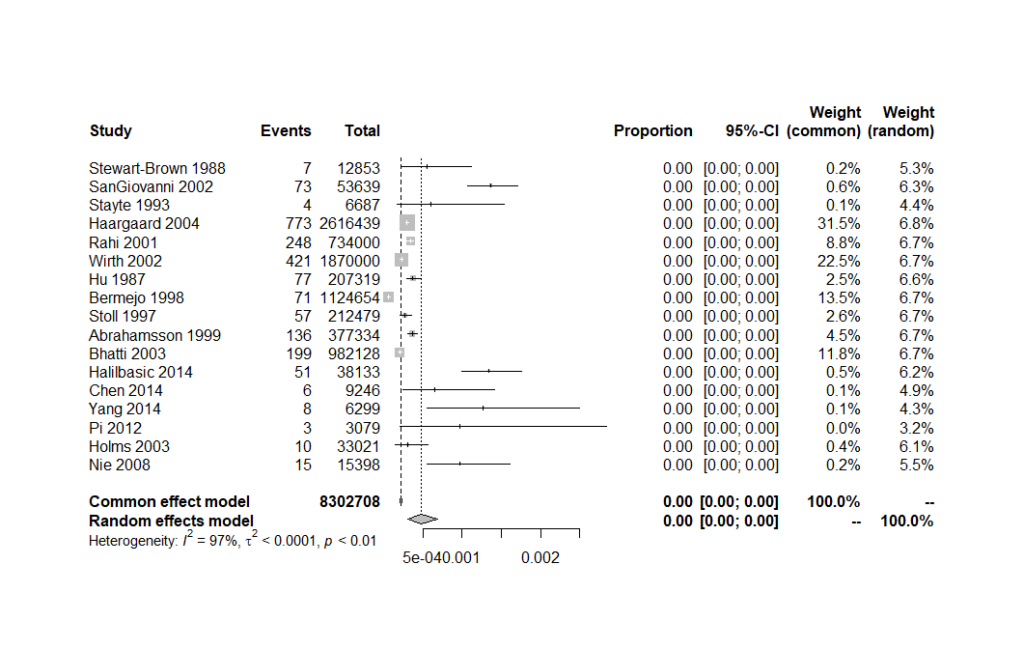
割合が小さすぎて、Proportion, 95%-CI の欄が、全部 0.00 になってしまっているのでいろいろと調整して、0 以外の数値が何か見えるようにしたほうが良いとは思う
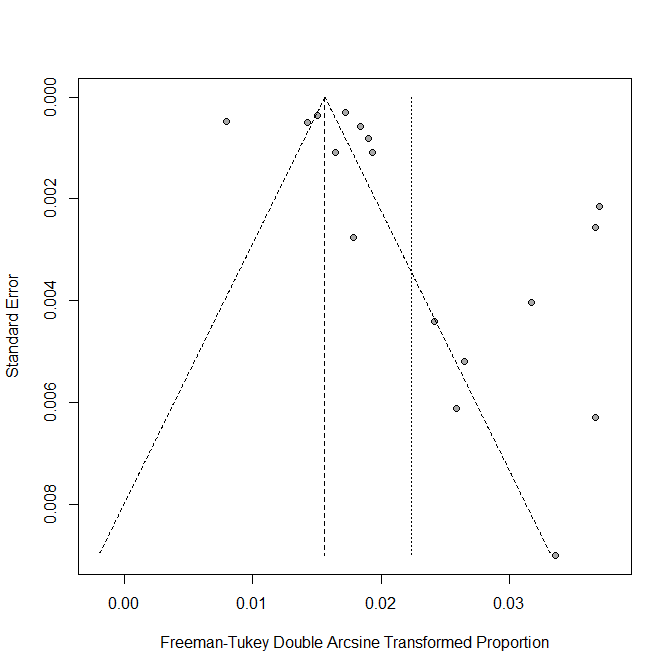
出版バイアスを確認するファンネルプロットは、以下のように書くと、描かれる
funnel(pes.summary)
ファンネルにおさまっていない感じであるし、左下がないのがよくわかるので、出版バイアスは少なからずありそうである
まとめ
R で割合のメタアナリシスの方法を解説した
metafor と meta の 2 つのパッケージを使えば、簡単に計算でき、きれいな図で出力できる
参考になれば
参考文献
(PDF) How to Conduct a Meta-Analysis of Proportions in R: A Comprehensive Tutorial








コメント