G*Power は、サンプルサイズ計算ソフトである
相関を計算するのに必要なサンプル数を計算するときの使い方を解説する
GPower で相関の必要サンプル数計算
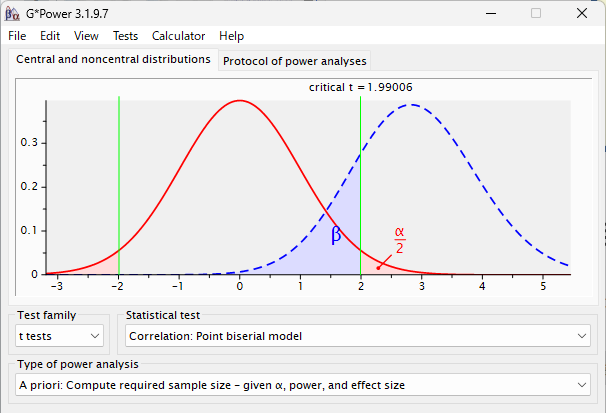
G*Power での設定は以下のように行う
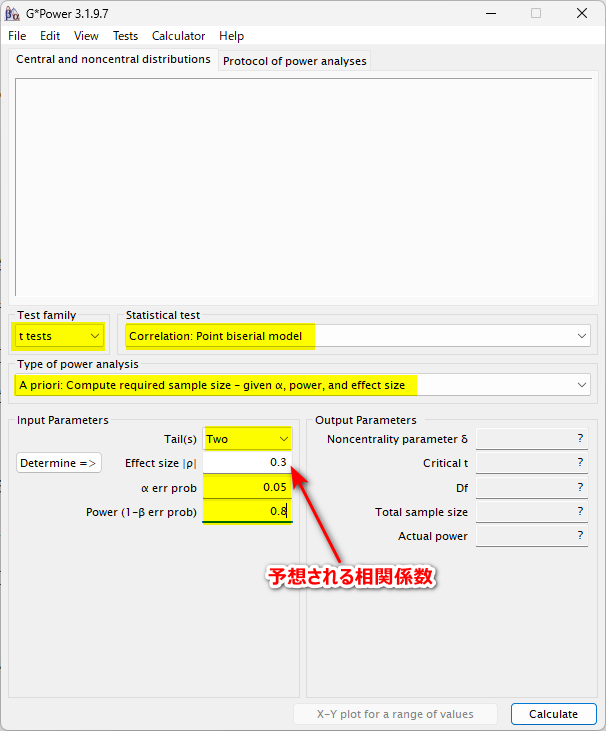
Effect size に予想される相関係数を入れる
0.3 とすると以下のように計算される
Calculate をクリックすると計算される
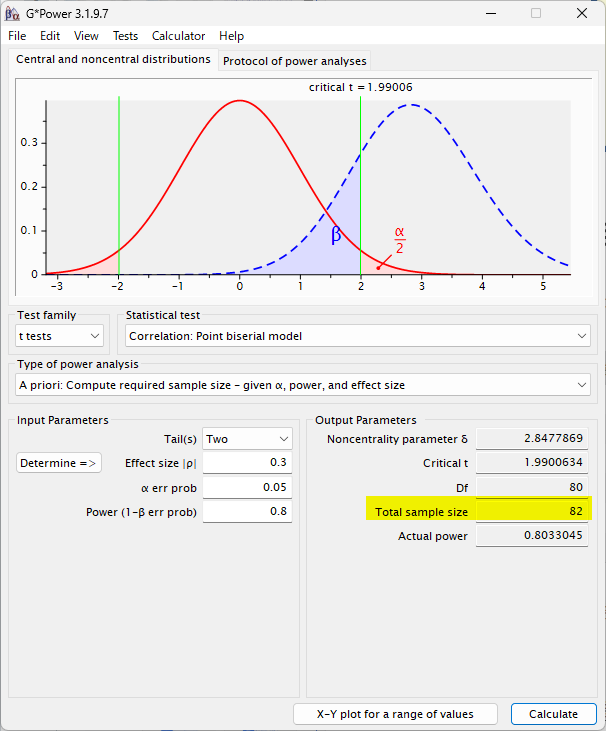
Total 82 例必要と計算される
予想される相関係数がわからない場合
相関係数の大きさを Effect size として、以下のような慣例的な基準がある
| Effect size | |
|---|---|
| small | 0.1 |
| medium | 0.3 |
| large | 0.5 |
small の場合は、779 例必要となる
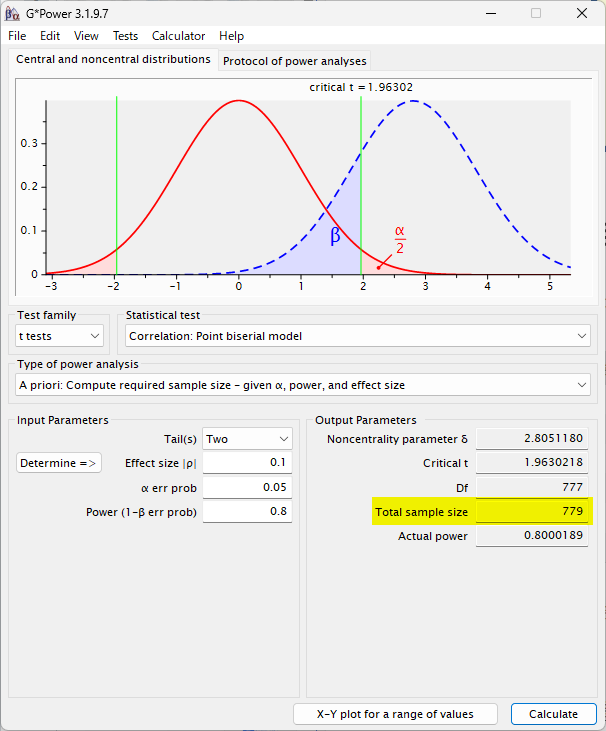
medium の場合は、上記のとおり、82 例である
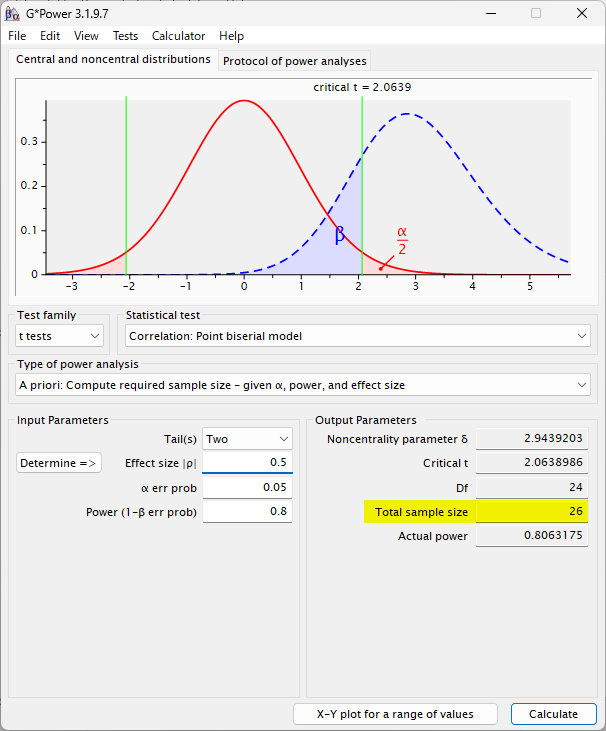
large の場合は、26 例でよい
論文への記載例
論文の記載例は以下のとおりである
サンプルサイズ計算は、G*Power 3.1.9.7 で行った(Faul 2007, Faul 2009)母相関係数の検定を両側検定で行うとし、想定される相関係数を 0.3、有意水準 5 %、検出力 80 % とすると、必要サンプルサイズは 82 例と計算された。
The sample size calculation was performed using G*Power 3.1.9.7 (Faul 2007, Faul 2009). Assuming a two-tailed test for the population correlation coefficient with an expected correlation coefficient of 0.3, a significance level of 5%, and a power of 80%, the required sample size was calculated to be 82 cases.
必要に応じて、想定される相関係数をどのように見積もったか、加筆してもよいだろう
計算のしくみをざっくり説明
計算の元は、母集団の相関係数の検定である
母集団の相関係数が 0 であるという帰無仮説を棄却するためには何例必要かという計算である
母集団から取り出したサンプルにおける相関係数が 0.1 だとすると、0 と違うというには、たくさんの症例数が必要という理屈になる
逆に 0.5 だとすると、0 と違うと言うのは簡単で、症例数も少なくて済む
ざっくり言うと、こういう理屈になっている
事後検出力の計算をする場合
統計解析を行った後に、統計学的有意にならず、事後検出力の計算が必要になることがある
その場合は、Type of power analysis のプルダウンメニューから、Post hoc を選択する
例えば、相関係数 0.5 で、症例数が 20 例だったとして、その場合の事後検出力は以下のとおり、0.685(68.5 %)と計算される
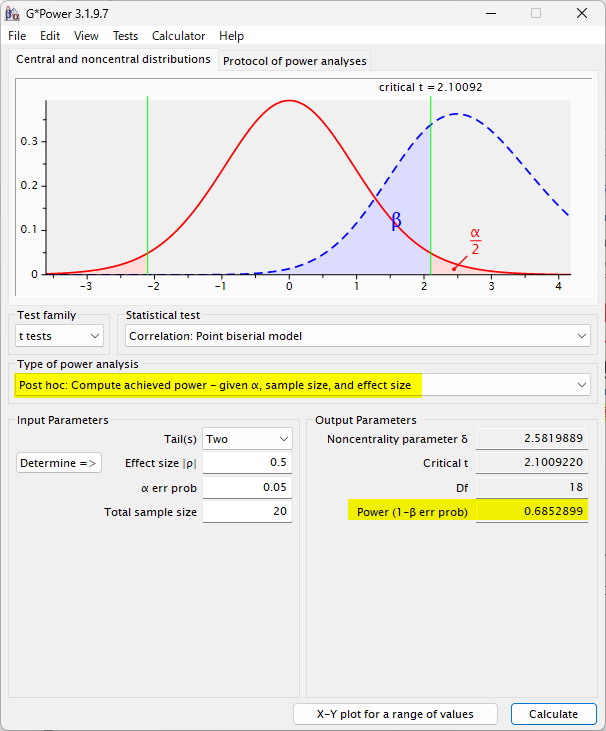
検出力は 80 %は欲しいので、理想的な状況には少し届かなかったことがわかる
この結果をもって、研究限界を考察することになる
まとめ
G*Power を使って相関係数の計算に必要なサンプル数を計算する方法を紹介した
事後検出力の計算方法も紹介した
参考になれば








コメント