Comparative Interrupted Time Series とは何か どんな時に使うのが良いか わかりやすく解説

Comparative interrupted time series (CITS) は、どんな分析方法で、どんなときに使うのが良いか？

CITSの前にITS

現実世界の状況として、集団全部に介入するということが起き、時系列データだけがあり、そのデータを分析せざるを得ないことはある。

そのような大規模介入の例として、集団ベースの健康介入、メディアキャンペーン、専門家のガイドラインの周知、あるいは、新たな法律や税制を導入して実施される公衆衛生政策の変更などがある。

このような１群しかない場合に、介入前後を比較する方法として Interrupted Time Series (ITS) がある。

ある時間間隔で目的変数が測定されているとして、独立変数は、調査開始からの年、介入前か後か、年数と介入の交互作用項の３つからなる、重回帰モデルで解析する。

ランダム化で比較していないが、介入前後の複数回のデータがある場合に取りうる、介入効果を推定する方法の一つと言える。

CITSはどんなときに使うのが良いか？

CITSは、ITSに比較対照となる統制群がおける場合の解析方法だ。

この方法を選択する場面は、以下のような状況が適している。

• RCTを実施するのが現実的でない。
• 処置（治療や介入）が集団レベルで施される（クラスタと言うとわかりやすいかもしれない）。
• 複数時点のデータを所持している。
• 処置以外は類似の複数群である。
• 処置としては同じ履歴とinstrumentation threatsを持つ（Instrumentation threats: 測定方法論的問題点とでも言えるか。内的整合性の脅威としてinstrumentationの違いや適切性が論じられているが、適切な日本語が見つからない）。
• 処置群（実験群、介入群と同じ意味合い）と統制群（コントロール群、比較対照群と同じ意味合い）ともに一貫したデータ測定がなされている。

グラフに示すとこんな感じのデータだ。

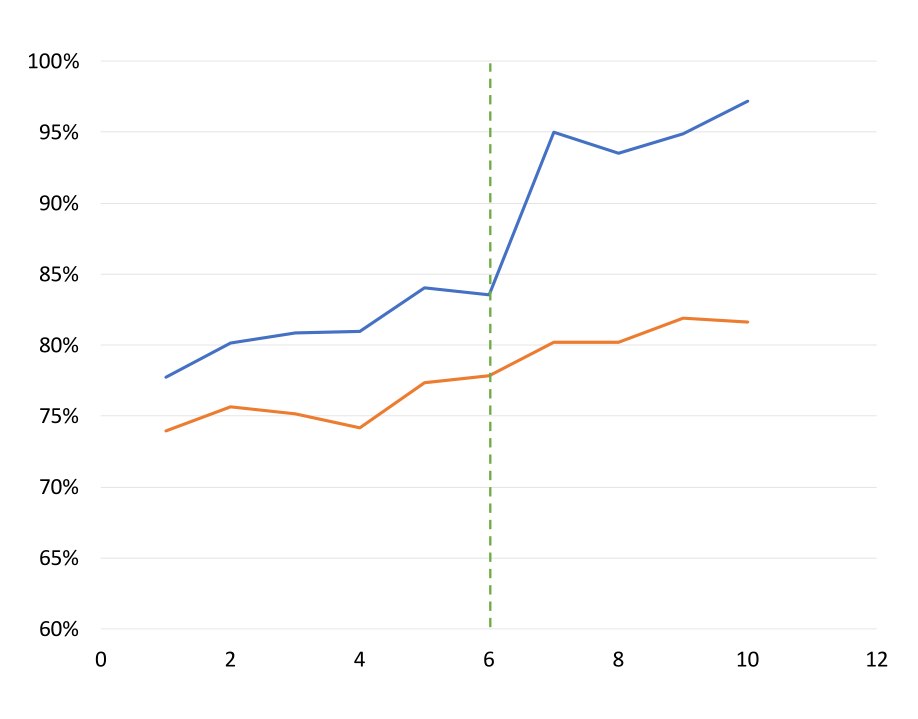
出典：https://cteresearchnetwork.org/sites/default/files/2020-11/CTERN-STI20-CITS-508.pdf 3ページ目

切片、傾き、介入のときの大きな変化などをイメージで表すと以下のようなグラフになる。

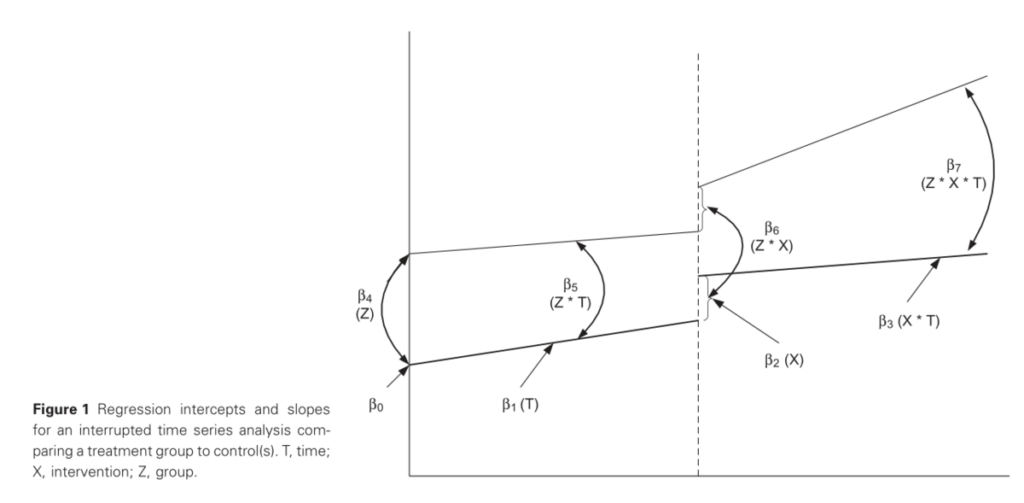
出典：http://lindenconsulting.org/documents/Weighted_TSA_Article.pdf Figure 1

ただし、ここで使っている変数名と以下で登場する変数名は異なるため、あくまでイメージとして見てほしい。

CITSはどんなときに適用できるか？

CITSが適用できる条件をまとめると以下のようになる。

• 複数時点の測定データがある。
• 処置群と統制群の両方の背景データがある。
• 介入前に少なくとも２時点分の測定値がある。
• より柔軟なモデルを用いるには、介入前のデータが少なくとも３時点分必要になる。

CITSの統制群はどのように選択するのか？

それでは、CITSの統制群をどのように選んだらよいのか？

よく用いられている方法は、次の 5 つである。

1. 処置を受けていない利用可能なすべての集団（Using All Available Nontreatment Samples）
2. 介入前の背景でマッチングして選択する（Matching）
3. 観察可能な特徴についてマッチする（Focal Selection）
4. 処置群と地理的に近い集団（Local）
5. FocalとLocalのミックス（Hybrid）

Hybridマッチングがバイアスを抑制するというエビデンスがある一方、他の方法それぞれはエビデンスがない。

CITSにおける処置効果の推定：Baseline Mean Model

CITSの推定値を回帰分析で求める。

モデル式は以下の通り。

$$ Y = \beta_0 + \beta_1 Z + \beta_2 Post + \beta_3 T + \beta_4 (Post \times T) + v + u $$

ここで、Zは各群の特徴セット、Postは介入後かどうかの変数、Tは処置群かどうか、vは群内誤差、uは平均ゼロの誤差。

わかりやすさ優先のために添え字はほぼ削除している。

式はイメージをつかむ目的にのみ登場させている。

興味のあるパラメータは$ \beta_4 $ ということになる。

CITSにおける処置効果の推定：Baseline Linear-Trend Model

このモデルは、前述のBaseline Mean Modelの拡張版で、時間 Time そのものを線形で投入している。

$$ Y = \beta_0 + \beta_1 Time + \beta_2 Z + \beta_3 Post + \beta_4 T + \beta_5 (Time \times T) + \beta_6 (Post \times T) + v + u $$

介入 Post と 処置 T の交互作用項に加えて、時間 Time と 処置 T の交互作用も投入している。

$\beta_1 $ が統制群の処置前の傾きになり、$ \beta_5 $ が処置群の処置後の傾きになる。

$ \beta_6 $ が処置の効果になる。

CITSにおける処置効果の推定：Baseline Nonlinear-Trend Model

これは上述のLinear-Trend Modelを非線形に拡張したモデルである。

モデル式は以下のようになる。

$$ Y = \sum{\beta Time} + \beta_{Post T} Post \times T + \sum{\beta S} + u $$

ここで、Sは処置群・統制群の群を指定している。これまでは T として処置群と統制群のみを区別していたが、処置群・統制群に含まれるクラスタ（例：学校）を指定している。

$ \beta_{Post T} $ が求めたい処置の効果になる。

この推定のために、より多くの介入前のデータが必要となるが、いくつあればよいかは決まっていない。

CITSにおける処置効果推定モデルの使い分け

それぞれのモデルはどんなときに使うのが良いか？

Baseline Mean Modelは、介入前のデータが変動なく平坦で、処置群と統制群が平行の場合に適切である。

Baseline Linear-Trend Modelは、介入前のデータにおいて処置群と統制群間で傾きが異なる場合が適切である。

Baseline Nonlinear-Trend Modelは、パターンが明らかでなく、解釈が難しい場合に適切である。

いずれの場合も、線形回帰モデルで解析すればよい。

まとめ

Comparative Interrupted Time Series CITS は、RCTが実施しにくい状況で、集団レベルで処置が施され、複数時点のデータが取得出来ていて、処置群・統制群ともに一貫してデータが取得出来ている状況において適切な方法である。

学校など施設単位の介入の効果を経年データを用いて解析する場面に適していると考えられる。

参考サイト（PDF）

https://cteresearchnetwork.org/sites/default/files/2020-11/CTERN-STI20-CITS-508.pdf

https://journals.sagepub.com/doi/pdf/10.1177/1536867X1501500208

http://lindenconsulting.org/documents/Weighted_TSA_Article.pdf