指数関数的に上昇するデータを共変量調整の回帰分析したい場合どのようにすればよいか?
ガンマ分布の一般化線形モデルを使えばできる。
指数関数的に上昇するデータに対して共分散分析をあてはめようとすると
サンプルデータは「データ解析のための統計モデリング入門」の第6章 ガンマ分布のGLMのデータ。

ランダム変数を生成して、2グループに分けた変数を付け足した。
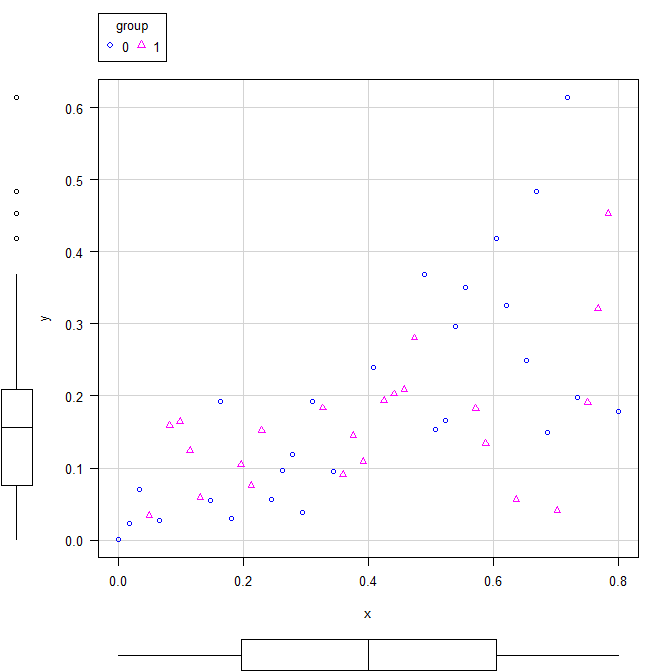
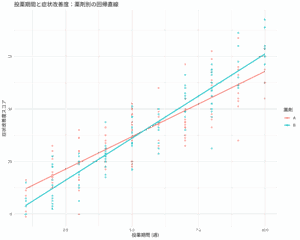
まず、EZRで散布図を描いたところ。
線形モデルで共分散分析をすると交互作用ありで解析不能と出る。

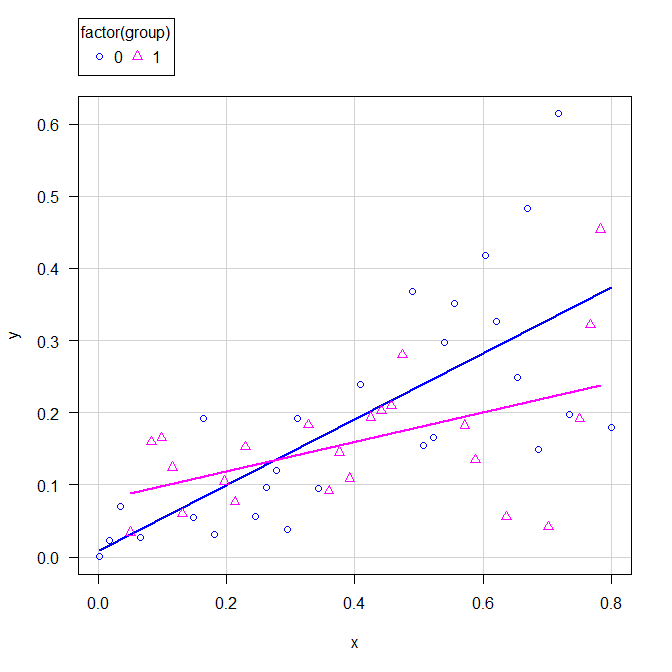
グループごとの回帰直線を引くとこのような感じになるが、フィットしていないことがわかる。
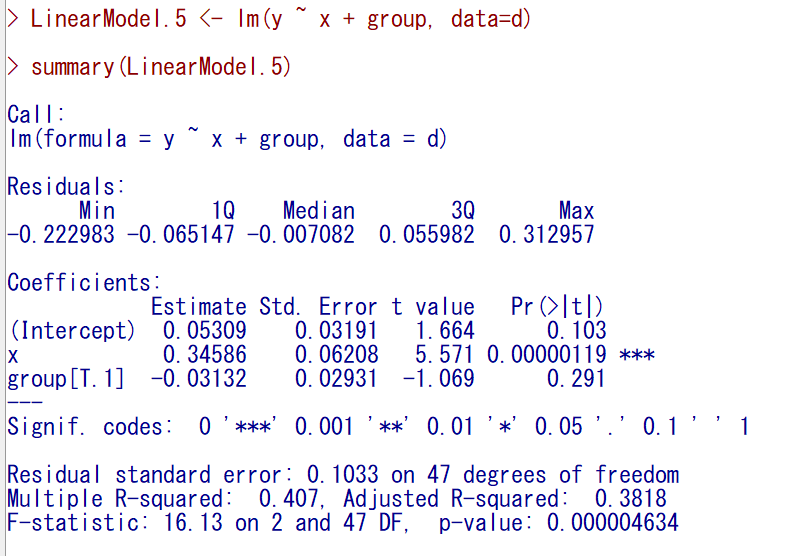
標準メニューの線形モデルでもやってみる。
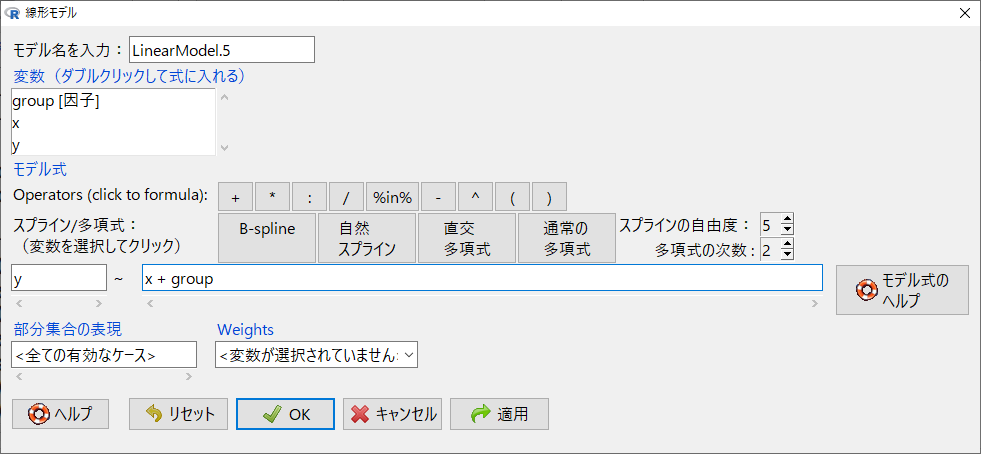
このように指定する。
すると無理やりかもしれないが計算できなくもない。
ちなみに、群は無視して、いわゆる単回帰分析をすると以下の通りで、こちらも計算できなくはない。
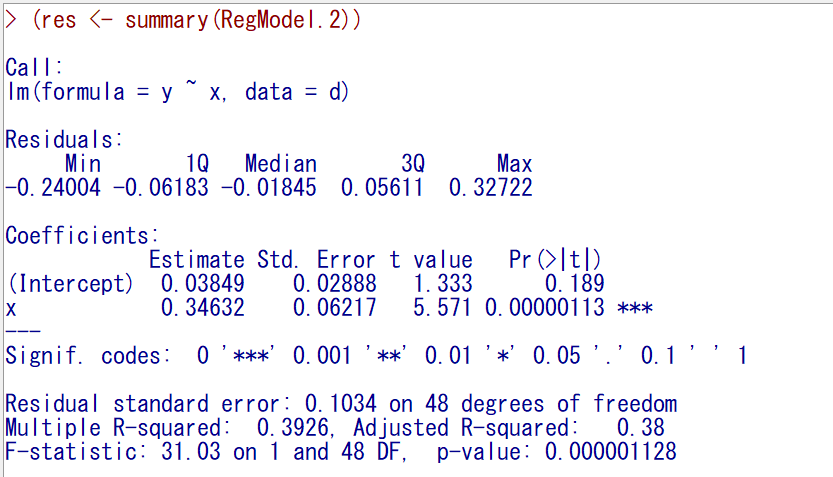
計算できることと、適切かどうかは、異なるため、最終的にはあてはまりが良いかどうかをよく確認したほうが良い。
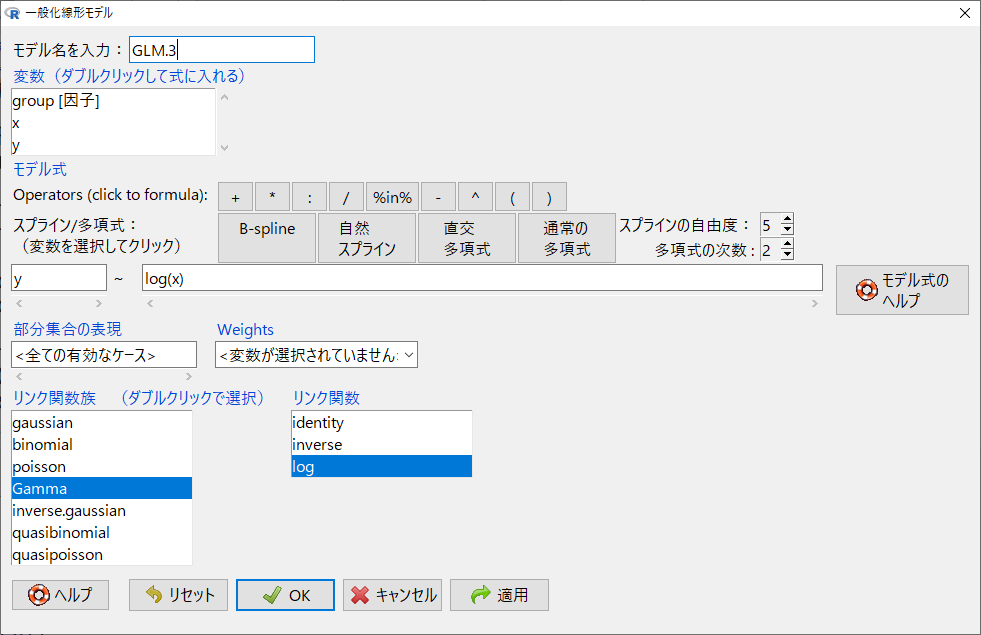
指数関数的に上昇するデータに対してガンマ分布の一般化線形モデルを当てはめる
EZRの標準メニューにある一般化線形モデルを開く。
目的変数をy, 説明変数をlog(x)として、リンク関数族をGamma、リンク関数をlogと指定してOKをクリック。
解析結果が出力される。
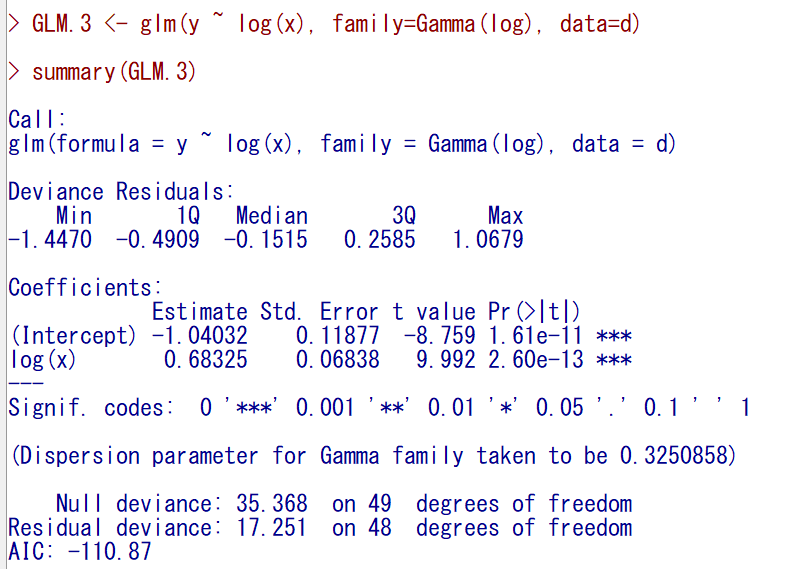
群別変数のgroupも入れてみる。
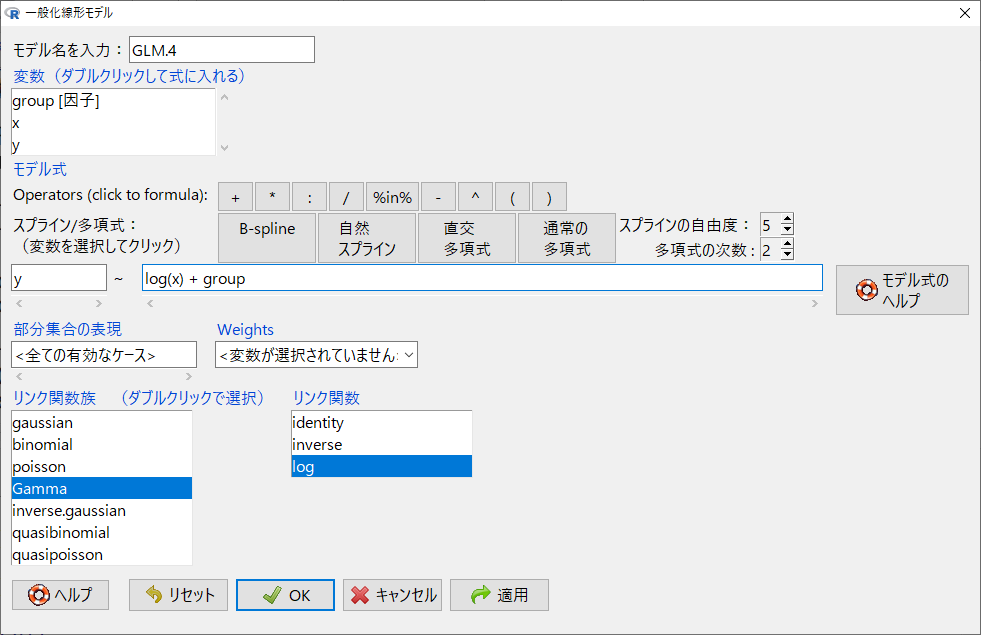
結果はこのように出力される。
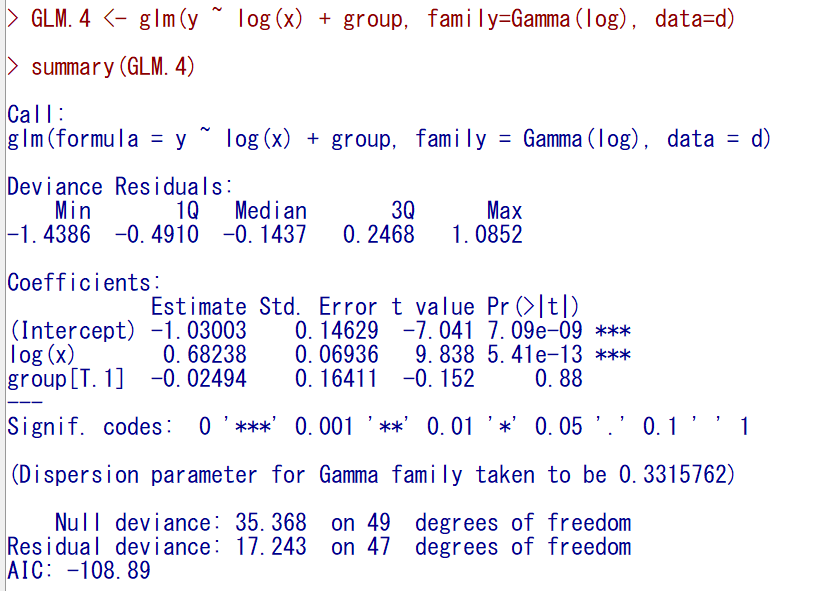
群別に異なるかどうかは、偏回帰係数が統計学的有意かどうかで判断できるが、群別変数なしモデルと群別変数ありモデルを比較することで意味があるかどうかを見ることもできる。
標準メニューの2つのモデルを比較を使う。
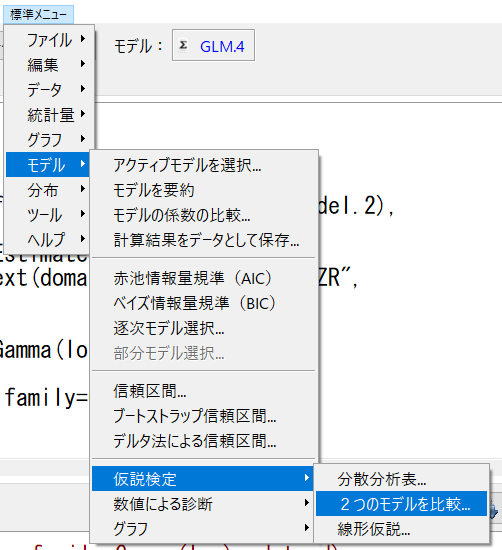
群別変数なしGLM.3と群別変数ありGLM.4を選択してOKをクリック。
Analysis of Devianceが実行されて、2つのモデルが異なるかどうかが示される。
この場合違いはないと判断できる。

AICで比較することもできる。
Rスクリプト窓に
AIC(GLM.3, GLM.4)
と書いて実行すると、以下のようにAICが並んで出力される。
群別変数がないGLM.3のほうが値が小さいため、当てはまりがよいことを示している。

線形モデルと一般化線形モデルの共分散分析の当てはまりを比較するとどうか?
AIC(GLM4. LinearModel.5)
一般化線形モデルのほうが当てはまりが良いことがわかる。

ちなみに単変量解析の結果をAICで比べてみると、どうなるか。
AIC(GLM3. RegModel.2)
こちらも一般化線形モデルのほうがずっと当てはまりが良いことがわかる。

一般化線形モデル内で交互作用項を扱うことができるか?
以下のように * (アスタリスク)を使うと交互作用項を投入できる。
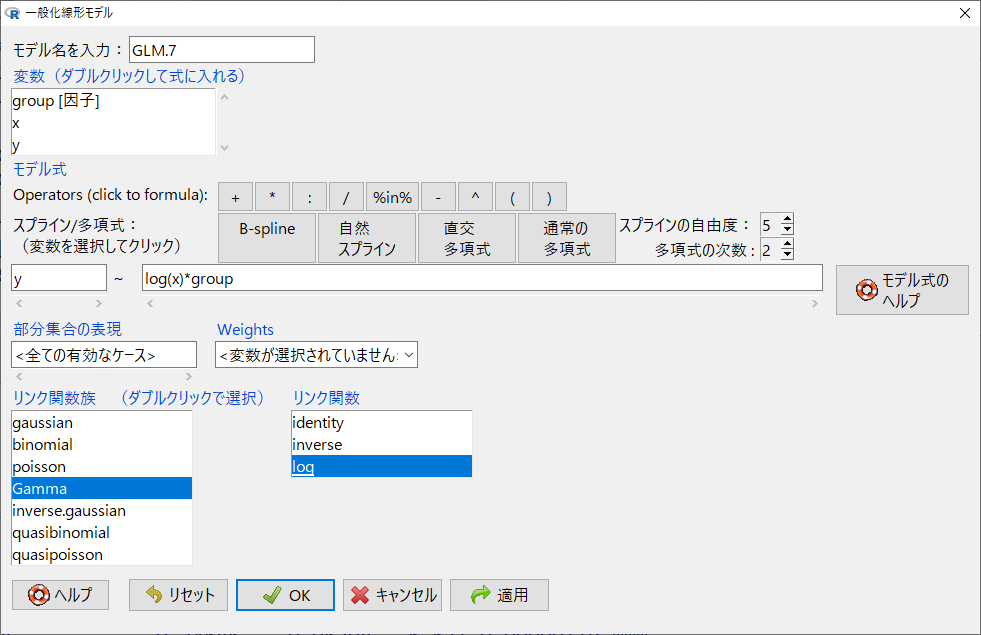
有意水準5%と考えると、赤矢印のように、交互作用項が統計学的に有意である。
つまりは、groupごとにlog(x)の偏回帰係数が異なるという結果になった。
この場合は、groupごとに解析しなおすほうがよい。
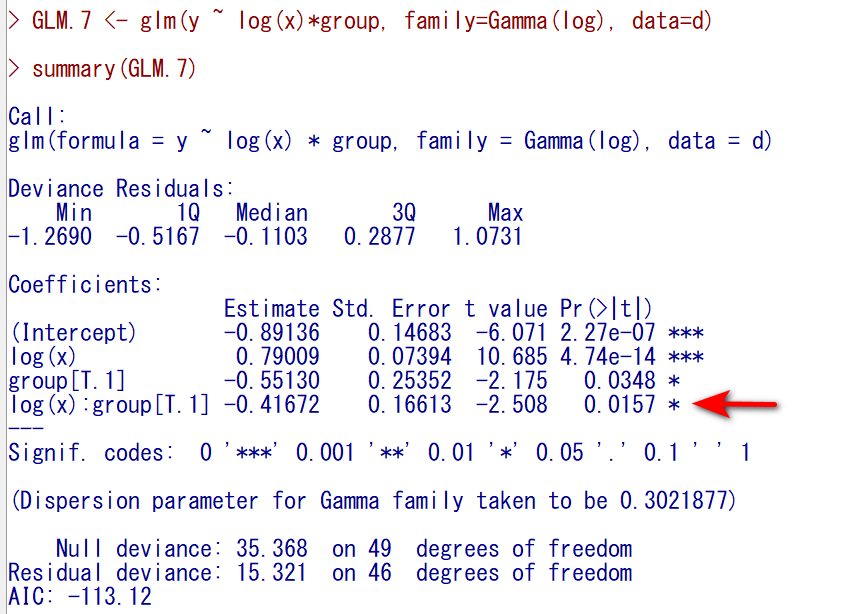
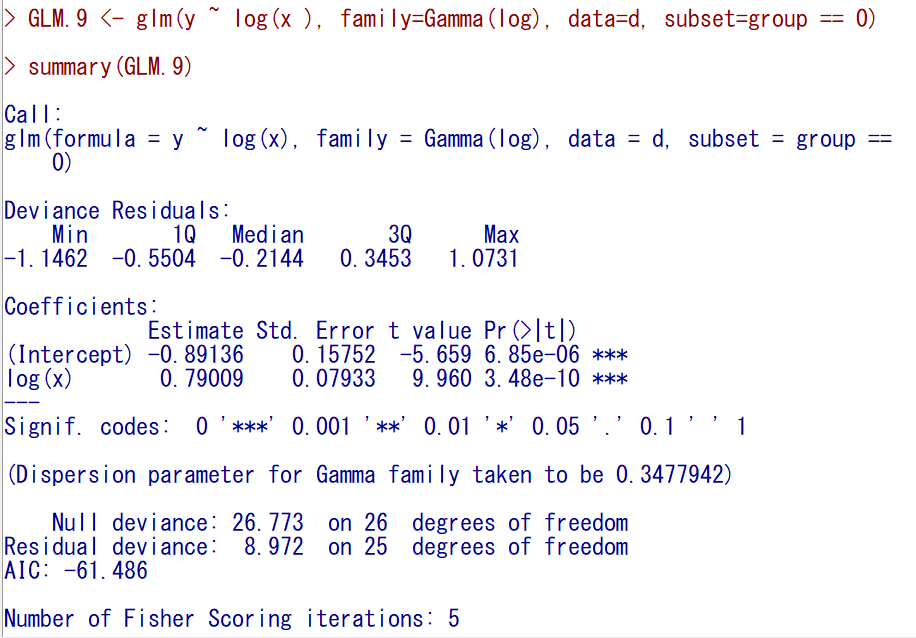
まずgroup == 0だけであてはめをおこなってみる。
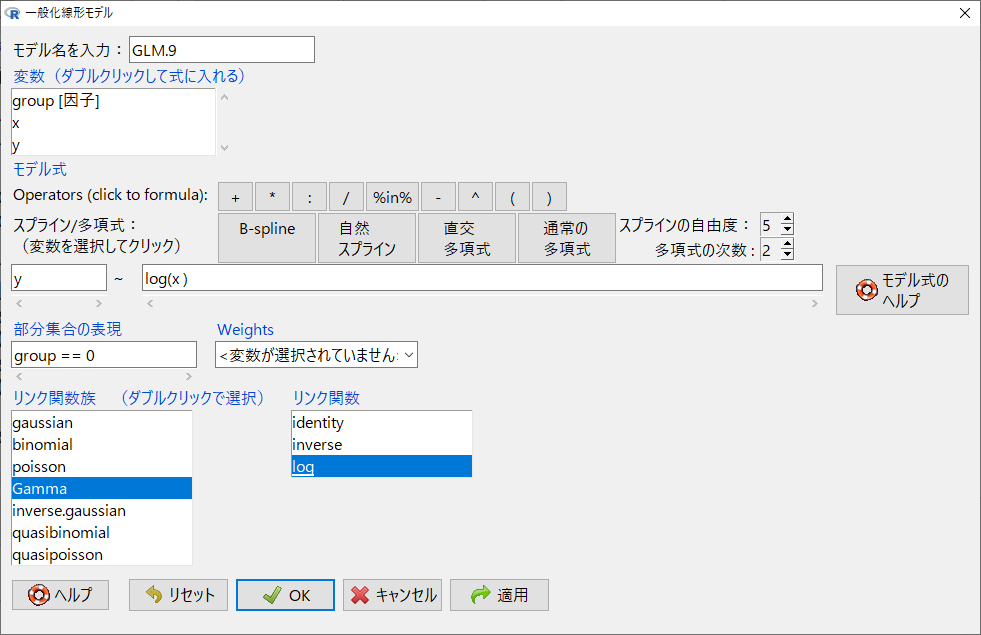
log(x)の回帰係数が0.79009である。
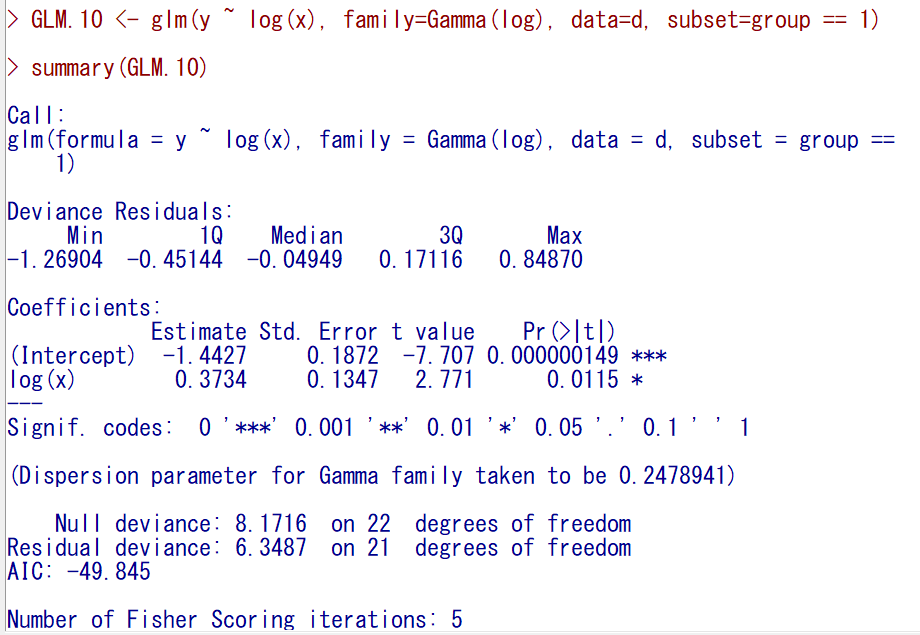
group == 1であてはめてみると以下のようになる。
回帰係数が0.3737で、有意確率も0.05を少し下回っただけである。
group == 0 とはだいぶ違うことがわかる。
上述した散布図で青〇がグループゼロで、ピンク△がグループ1である。
確かに青〇のグループゼロのほうがXでYを説明できるという関係が強そうに見える。
当てはまりをAICで見てみると、group==0のほうが値が小さく当てはまりが良いことがわかる。
AIC (GLM.9, GLM.10)

信頼区間を表示させるには?
推定したパラメータの信頼区間を得たい場合は、標準メニューから信頼区間メニューを使う。
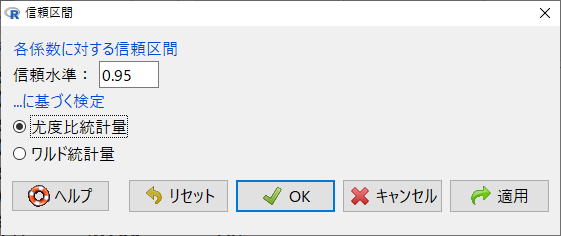
尤度比統計量とワルド(Wald)統計量の2つに基づく計算が実施可能である。
今回のGLM.7(交互作用項入りモデル)データでは、どちらも同じ結果になった。


まとめ
指数関数的に上昇するデータを予測する回帰モデルには、ガンマ分布を用いた一般化線形モデルがある。
共変量として群別の変数を投入することもできる。
つまりは、指数関数的に上昇するデータに対する共分散分析を行ったことになる。
また、交互作用項も扱える。
信頼区間も算出できる。
参考書籍
データ解析のための統計モデリング入門

EZR公式マニュアル








コメント