複数の研究を統合するメタアナリシス。
固定効果モデルと変量効果モデルが存在する。
統合する際の重みが異なるのが一番の違い。
どんな重み計算をしているのか?
メタアナリシスとは?
システマティックレビューを行った複数の研究の効果量を統合する解析方法。
メタアナリシスの過去記事はこちらからどうぞ。
メタアナリシスはどんな計算をしているのか?
メタアナリシスは統合した点推定値と区間推定を行っている。
その際に、個々の研究に適切な重みを付けた重み付け平均を計算している。
統合方法には、固定効果モデルと変量効果モデルがあって、それぞれ重みが異なる。
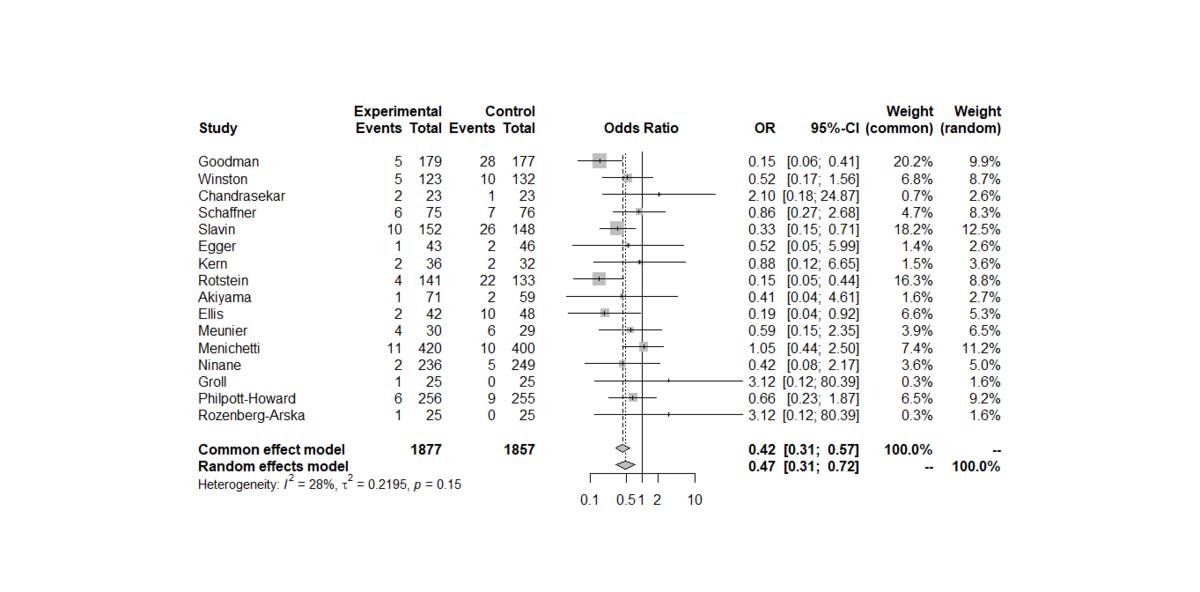
例えば、EZR公式マニュアルのサンプルデータを用いたフォレストプロットを見ると、右端のWeight(common), Weight(random)で値が異なっているのがわかる。
Weight(common)が固定効果モデルの重みで、Weight(random)が変量効果モデルの重みである。
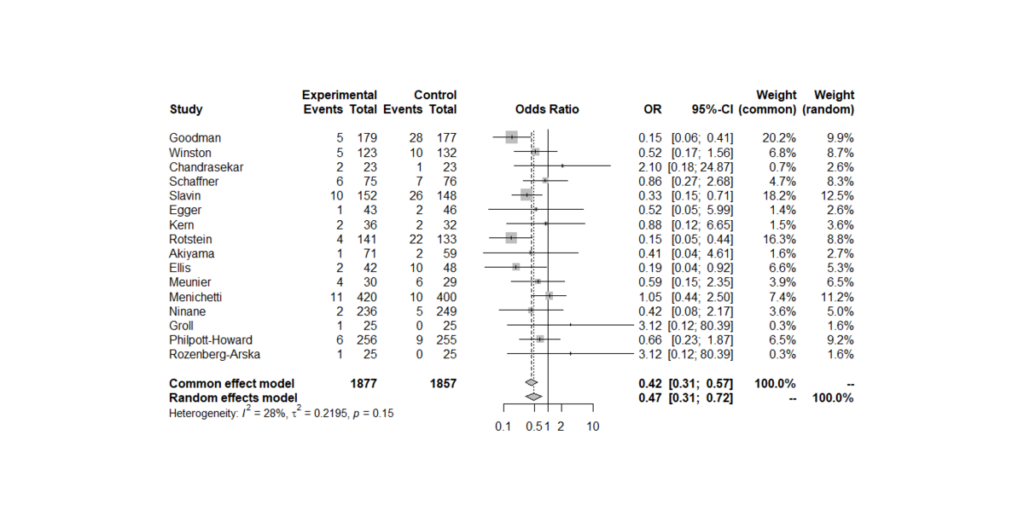
実際どんな計算をしているか改めて確認してみる。
メタアナリシスの固定効果モデルの重み
固定効果モデルの重みは、標準誤差の2乗の逆数である。
標準誤差は、点推定値の推定精度を表し、サンプルサイズが大きいと小さくなる。
標準誤差の2乗の逆数ということは、サンプルサイズが大きく影響力の大きい研究は、小さい標準誤差なので、その2乗の逆数は、大きな重みということになる。
単純な場合を考えて、粗オッズ比を統合するとすると、まずオッズ比と標準誤差は以下のように計算できる。
ある研究の2×2分割表
| 疾病あり | 疾病なし | |
|---|---|---|
| 曝露あり | a | c |
| 曝露なし | b | d |
オッズ比 OR
$$ OR = \frac{ad}{bc} $$
(のちの計算では対数をとった $\log{OR}$ で登場する。)
標準誤差 se
$$ se = \sqrt{\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d}} $$
固定効果モデルの各研究の重みは以下のように計算している。
重み w
$$ w = \frac{1}{se^2} $$
メタアナリシスの変量効果モデルの重み
重みの計算式にたどり着く前に、出発点として、均質性(もしくは異質性)の検定統計量Q1を計算する。
均質性の検定統計量Q1を計算するときには、固定効果モデルでの重み付け平均点推定値が求まっていないといけない。
固定効果モデルでの統合点推定値 $ \log{OR_f} $(添え字の f は固定Fixedを表している)
(計算の都合上対数のままにする)
$$ \log{OR_f} = \frac{\sum{w \times \log{OR}}}{\sum w} $$
均質性の検定統計量Q1
$$ Q_1 = \sum{w \times (\log{OR} – \log{OR_f})^2} $$
均質性の検定統計量Q1と各研究の重み w を使って、研究間のばらつきの大きさ τ(タウ)2乗を計算する。
$$ \tau^2 = \frac{Q_1 – (k – 1)}{\sum{w} – \frac{\sum{w^2}}{\sum w}} $$
kは統合する研究の数である。
タウ2乗はマイナスになることもあるが、その場合はゼロとする。
つまりゼロの時は研究間のばらつきが大きくなく、タウ2乗を加える必要がないという意味になる。
このタウ2乗を考慮した方法がDerSiminian-Laird (DL) の方法で、重み計算の際に分母にタウ2乗を足す。
$$ w_{DL} = \frac{1}{\tau^2 + se^2} $$
すると、研究間のばらつきが大きくタウ2乗が大きい場合、重みは小さくなる。
このタウ2乗が固定効果モデルの重みと異なる部分である。
標準誤差が大きい(重みが小さい)研究の場合、タウ2乗はそれほど貢献しないが、標準誤差が小さい(重みが大きい)研究の場合は、タウ2乗の効果は相対的に大きくなる。
さらに、このタウ2乗を初期値にして、制限付き最尤推定量(REML estimator) を求めると、EZRのメタアナリシスの結果になる。(もしかすると初期値は違うかもしれない。)
REMLは、繰り返し計算を要する。
そして繰り返し計算する式自体は単純には書き表せない。
DLのタウ2乗をより適切に磨き上げた、よりよい値と思う程度でよいだろう。
REML法については以下を参照。(初期値はDLのタウ2乗とは異なるかもしれないと思うのは、以下のブログ記事の最後で、計算が合わなかったことに起因する。)
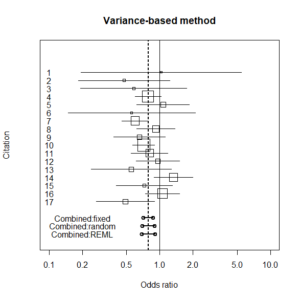
まとめ
メタアナリシスにおける固定効果モデルと変量効果モデルの重みの違いを改めて確認してみた。
固定効果モデルの重みは、研究内のばらつきの指標(推定精度の指標)として標準誤差を用いている。
変量効果モデルの重みは、標準誤差に加えて、タウ2乗という研究間のばらつきを表す指標を考慮している。
タウ2乗が大きく研究間のばらつきが大きい場合、固定効果で大きな重みがあった研究が相対的に軽くなる理屈になっている。
参考になれば。
おすすめ書籍








コメント