オッズ比のサンプルサイズ計算の方法
オッズ比計算のためのサンプルサイズ計算・検出力計算のための準備
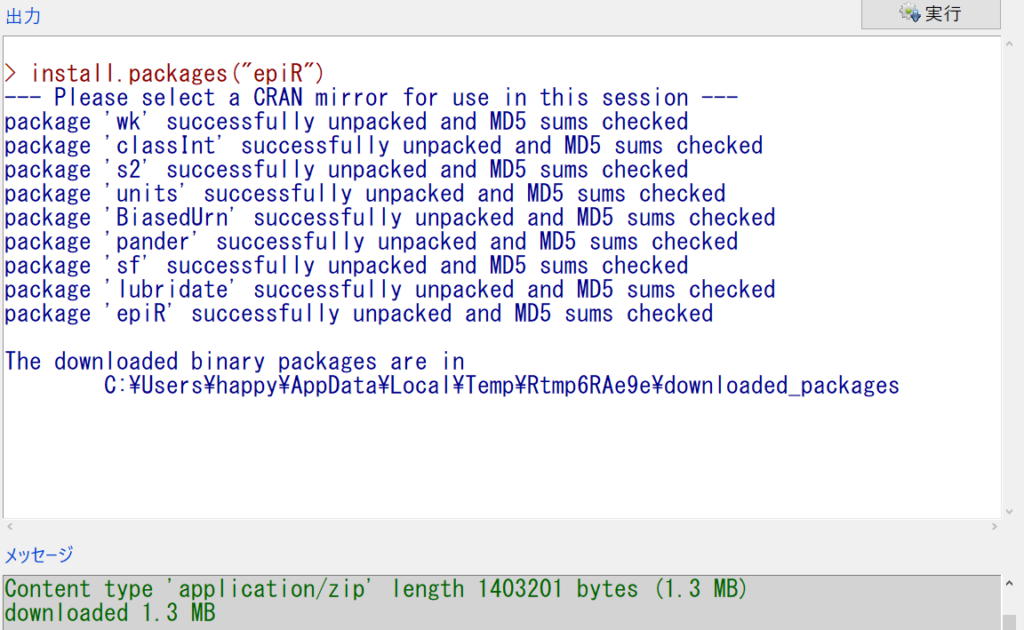
EZRにepiR パッケージをインストールする。
Rスクリプト窓にinstall.packages("epiR")と書いて実行をクリック。
ダウンロード元を選ぶ(2024 年 10 月現在、Tokyo は利用不可で、Yonezawa のみ)
インストール後の状態。
使うときは事前にlibrary(epiR)を実行する。
オッズ比計算のサンプルサイズ計算・検出力計算するための関数は?
epi.sscc()という関数を使う。
設定できる変数は様々あるが、マッチしていない通常のオッズ比の場合、覚えるべきは、
- OR(オッズ比)
- p0(コントロールで曝露している人の割合)
- n(ケースとコントロールの合計のサンプルサイズ)
- power(検出力)
- r(ケースを1としたときのコントロールの数)
の5つ。
epi.sscc(OR, p0, n, power, r = 1, rho.cc = 0, design = 1, sided.test = 2,
nfractional = FALSE, conf.level = 0.95, method = "unmatched", fleiss = FALSE)
オッズ比計算のサンプルサイズ・検出力を計算してみる
マッチしていない通常のデータで、オッズ比を計算するとして、想定オッズ比が1.5、コントロール群の曝露が3割、30%=0.3、検出力80%(慣例)、ケースとコントロールの比が1とすると、合計850人必要と計算される。
上記5つの要素のうち、求めたい要素を NA としておくことがこの関数の仕様である。
> epi.sscc(OR=1.5, p0=0.3, n=NA, power=0.8, r = 1)
$n.total
[1] 850
$n.case
[1] 425
$n.control
[1] 425
$power
[1] 0.8
$OR
[1] 1.5
サンプルサイズが1000例とすると、検出力は86%となる。
> epi.sscc(OR=1.5, p0=0.3, n=1000, power=NA, r = 1)
$n.total
[1] 1000
$n.case
[1] 500
$n.control
[1] 500
$power
[1] 0.8600573
$OR
[1] 1.5
ケースとコントロールの比を 1:2 とすると、ケースが321例、コントロールが642例の計963例必要と計算される。
ケースは少なくて済むが、全体のサンプルサイズは増える。
> epi.sscc(OR=1.5, p0=0.3, n=NA, power=0.8, r = 2)
$n.total
[1] 963
$n.case
[1] 321
$n.control
[1] 642
$power
[1] 0.8
$OR
[1] 1.5
合計サンプルサイズが1000例として、ケースとコントロールが 1:2 とすると、検出力は約81%になる。
1:1 のときが86%なので、少し下がったが、それでも80%以上。
> epi.sscc(OR=1.5, p0=0.3, n=1000, power=NA, r = 2)
$n.total
[1] 1000
$n.case
[1] 334
$n.control
[1] 666
$power
[1] 0.8149441
$OR
[1] 1.5
まとめ
オッズ比のためのサンプルサイズ・検出力計算は、epiRパッケージのepi.sscc()関数を使う。
参考になれば。
参考文献
Package ‘epiR’
https://cran.r-project.org/web/packages/epiR/epiR.pdf
おすすめ書籍









コメント