ログランク検定とは、生存時間解析で、二群以上のグループがある場合に、グループ間で統計学的に差があるかを検討する方法。
R での方法を解説。
R でログランク検定をする場合の関数は?
R でログランク検定をする場合、survival パッケージのsurvdiff()関数を使う。
survival パッケージは最初からインストールされているパッケージで、使うときにlibrary()で呼び出す。
library(survival)
survdiff()はどうやって使う?
survdiff()は、Surv()と組み合わせて使うことになる。
Surv()は、生存時間データとエンドポイントデータを使って、生存時間解析に使えるデータに変換する関数。
Surv()については、こちらも参照。
survdiff(Surv(時間データ, イベントデータ) ~ グループ変数)
という形が基本形。
survival パッケージの ovarian データを使って、ログランク検定をしてみる。
ovarian データセットは、卵巣がんの治療を、二種類の治療法にランダムに振り分けた時の試験結果データ。
futimeが生存時間データ、fustatが打ち切りか、死亡か、rxは二つの治療法のどちらを受けたかを表す変数。
ovarian データセットの内容
ovarian データセットの先頭部分を表示してみる。以下のようなデータであることがわかる。futimeは日数。
> head(ovarian)
futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5 431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2
生存時間データとイベントデータをSurv()してみる
まずSurv()をしてみる。
> Surv(ovarian$futime,ovarian$fustat)
[1] 59 115 156 421+ 431 448+ 464 475 477+ 563
[11] 638 744+ 769+ 770+ 803+ 855+ 1040+ 1106+ 1129+ 1206+
[21] 1227+ 268 329 353 365 377+
数値は生存日数で、+がついている日数は観察打ち切りの日数である。
その日数までは生きていたことはわかるが、それ以降の情報がないという意味になる。
これを打ち切り(censoring、censored、センサリング、センサード)データと呼ぶ。
survfit()でグループごとのカプランマイヤー曲線を描いてみる
検定の前にカプランマイヤー曲線で図示してみる。
二種類の治療でどのくらい異なるのか、生存曲線を書いてみる。
survfit1 <- survfit(Surv(futime,fustat)~rx, data=ovarian)
plot(survfit1,las=1,xlab="Survival Time (days)", ylab="Overall Survival", col=2:3)
legend("topright", paste("Treatment=",1:2,sep=""), lty=1, col=2:3)
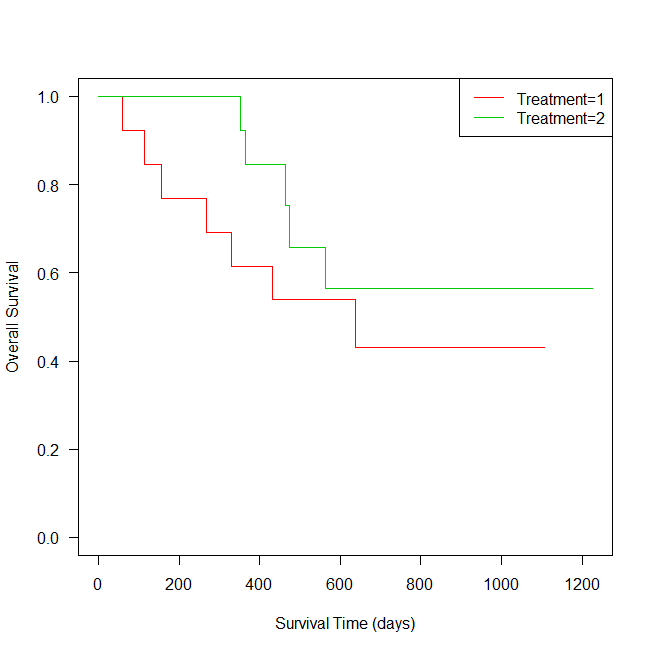
Treatment1よりも2のほうが生存確率が高いことがわかる。
統計学的に有意な差があるのかどうか気になるところだ。
survdiff()でログランク検定をしてみる
survdiff()を使って、ログランク検定をしてみる。
> survdiff(Surv(futime,fustat) ~ rx, data=ovarian)
Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)
N Observed Expected (O-E)^2/E (O-E)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06
Chisq= 1.1 on 1 degrees of freedom, p= 0.3
結果として、p=0.3で、統計学的有意ではない。
サンプルサイズの問題か、effect sizeの問題かは不明だが、カプランマイヤー曲線では差があるように見えるだけに惜しい気がする。
三群以上のログランク検定
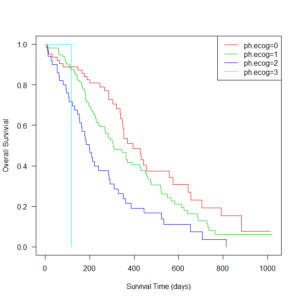
ところで、survival パッケージの肺がんデータでECOG performance score(四群)の差を検定してみると以下のようになる。
肺がんデータのカプランマイヤー曲線についてはこちらを参照。

> survdiff(Surv(time,status)~ph.ecog, data=lung)
Call:
survdiff(formula = Surv(time, status) ~ ph.ecog, data = lung)
n=227, 1 observation deleted due to missingness.
N Observed Expected (O-E)^2/E (O-E)^2/V
ph.ecog=0 63 37 54.153 5.4331 8.2119
ph.ecog=1 113 82 83.528 0.0279 0.0573
ph.ecog=2 50 44 26.147 12.1893 14.6491
ph.ecog=3 1 1 0.172 3.9733 4.0040
Chisq= 22 on 3 degrees of freedom, p= 7e-05
結果として、$ p = 7 \times 10^{-5} = 0.00007 $ なので、統計学的有意にグループ間で異なっていた。
ログランク検定をStep by stepでやってみる
survdiff() 関数を使わずにログランク検定をしてみるとどうなるか?
上述の ovarian データを使ってやってみた。
ovarian データを加工する
生存時間データ、イベントデータ、治療群データの三変数に絞り、生存時間が短い順に並べ替える。
治療群1と2にわけたデータも作成する。
dat <- ovarian[,c(1,2,5)]
dat0 <- dat[order(dat$futime), ]
dat1 <- subset(dat0, dat0$rx==1)
dat2 <- subset(dat0, dat0$rx==2)
観察・期待・at risk人数を計算する
各群のイベント観察データ(人数)をO1j、O2jとする。
各群の「イベントが起きた時点」の「イベントが起きうる(at risk)」人数をN1j、N2jとする。
各群の「イベントが起きた時点」のイベントの期待値をE1j、E2jとする。
イベント観察データ(O)の加工
O1jとO2jのそれぞれの合計をO1、O2とする。
O1は治療群1のイベント発現人数で7人、O2は治療群2のイベント発現人数で5人である。
O1j <- ifelse(dat0$fustat==1 & dat0$rx==1,1,0)
O2j <- ifelse(dat0$fustat==1 & dat0$rx==2,1,0)
O1 <- sum(O1j)
O2 <- sum(O2j)
At risk 人数データ(N)の加工
At riskの人数は、最初は全員だが、イベントが発現した後は、イベント発現者は除かれていく。
人数はだんだん減っていく。
N1j <- rep(0,length(dat0$fustat))
N2j <- rep(0,length(dat0$fustat))
N1j[1] <- length(dat1$fustat)
N2j[1] <- length(dat2$fustat)
for (j in 2:length(dat0$fustat)){
ifelse(dat0$rx[j-1]==1, N1j[j] <- N1j[j-1]-1, N1j[j] <- N1j[j-1])
ifelse(dat0$rx[j-1]==2, N2j[j] <- N2j[j-1]-1, N2j[j] <- N2j[j-1])
}
イベント期待値データ(E)の計算
イベントが発現した時点における、各群のat risk 人数の、全体 at risk 人数に対する割合に合わせて、期待されるイベント数が計算できる。
Oj <- O1j + O2j
Nj <- N1j + N2j
E1j <- Oj*N1j/Nj
E2j <- Oj*N2j/Nj
E1 <- sum(E1j)
E2 <- sum(E2j)
期待値の合計は治療群1で5.23人、治療群2で6.77人と計算され、survdiff()の結果と一致する。
治療群1の観察値O1が7人、治療群2の観察値O2が5人であるので、少しずつずれているのがわかる。
> E1
[1] 5.233531
> E2
[1] 6.766469
加工・計算した出来上がりのデータセット
上記で作成したデータを並べてみると以下のようになる。
> cbind(dat0,O1j,O2j,Oj,N1j,N2j,Nj,E1j,E2j)
futime fustat rx O1j O2j Oj N1j N2j Nj E1j E2j
1 59 1 1 1 0 1 13 13 26 0.5000000 0.5000000
2 115 1 1 1 0 1 12 13 25 0.4800000 0.5200000
3 156 1 1 1 0 1 11 13 24 0.4583333 0.5416667
22 268 1 1 1 0 1 10 13 23 0.4347826 0.5652174
23 329 1 1 1 0 1 9 13 22 0.4090909 0.5909091
24 353 1 2 0 1 1 8 13 21 0.3809524 0.6190476
25 365 1 2 0 1 1 8 12 20 0.4000000 0.6000000
26 377 0 2 0 0 0 8 11 19 0.0000000 0.0000000
4 421 0 2 0 0 0 8 10 18 0.0000000 0.0000000
5 431 1 1 1 0 1 8 9 17 0.4705882 0.5294118
6 448 0 1 0 0 0 7 9 16 0.0000000 0.0000000
7 464 1 2 0 1 1 6 9 15 0.4000000 0.6000000
8 475 1 2 0 1 1 6 8 14 0.4285714 0.5714286
9 477 0 1 0 0 0 6 7 13 0.0000000 0.0000000
10 563 1 2 0 1 1 5 7 12 0.4166667 0.5833333
11 638 1 1 1 0 1 5 6 11 0.4545455 0.5454545
12 744 0 2 0 0 0 4 6 10 0.0000000 0.0000000
13 769 0 2 0 0 0 4 5 9 0.0000000 0.0000000
14 770 0 2 0 0 0 4 4 8 0.0000000 0.0000000
15 803 0 1 0 0 0 4 3 7 0.0000000 0.0000000
16 855 0 1 0 0 0 3 3 6 0.0000000 0.0000000
17 1040 0 1 0 0 0 2 3 5 0.0000000 0.0000000
18 1106 0 1 0 0 0 1 3 4 0.0000000 0.0000000
19 1129 0 2 0 0 0 0 3 3 0.0000000 0.0000000
20 1206 0 2 0 0 0 0 2 2 0.0000000 0.0000000
21 1227 0 2 0 0 0 0 1 1 0.0000000 0.0000000
検定統計量 カイ二乗値と有意確率の計算
検定統計量は、観察値と期待値の差の2乗を期待値で割った値を各群で求め、合計する。
(O1-E1)^2/E1 + (O2-E2)^2/E2
計算結果のカイ二乗 $ \chi^2 $ はsurvdiff()の結果と一致して約1.1となった。
> (O1-E1)^2/E1 + (O2-E2)^2/E2
[1] 1.057393
自由度1で検定すると、上側有意確率は約0.3となる。これもsurvdiff()の結果と一致した。
> pchisq(1.057393,1,lower.tail=FALSE)
[1] 0.3038105
まとめ
Rで、二群以上の生存について統計学的に異なるかどうかを検定するログランク検定を行ってみた。
ログランク検定は、カイ二乗値を使った検定である。
ログランク検定をsurvdiff()を使わずにStep by stepでやってみると、実際にどんな計算をしているかがわかる。
イベントが起きた時点の観察値、at risk 人数から、イベントの期待値を計算し、$ \chi^2 $ を計算する。
検定は自由度1の $ \chi^2 $ 検定だ。
観察値が期待値に比べて大きく離れた場合、$ \chi^2 $ 値が大きくなり、統計学的有意と判断できる。
つまり、群間に統計学的に有意な差があるという結論になる。









コメント
コメント一覧 (1件)
[…] R でログランク検定を行う方法 […]