R で漸近分散法でオッズ比を統合するメタアナリシス

メタアナリシスのためにオッズ比を統合したい場合で、それぞれの研究のサンプルサイズが大きい場合、オッズ比の対数が漸近的に正規近似できる。

個々の研究のサンプルサイズが大きい場合は、漸近分散法を使う。

使用するデータの準備

データは以下の通り。

a <- c(3,7,5,102,28,4,98,60,25,138,64,45,9,57,25,65,17)
n1 <- c(38,114,69,1533,355,59,945,632,278,1916,873,263,291,858,154,1195,298)
c <- c(3,14,11,127,27,6,152,48,37,188,52,47,16,45,31,62,34)
n0 <- c(39,116,93,1520,365,52,939,471,282,1921,583,266,293,883,147,1200,309)
dat <- data.frame(a,n1,c,n0)

各試験のオッズ比と95%信頼区間を計算する

a, b, c, d, tn, lgor, se, low, uppは以下のことを表している。

a, b, c, dは2×2の分割表のマス目の名前。tnはサンプルサイズ。

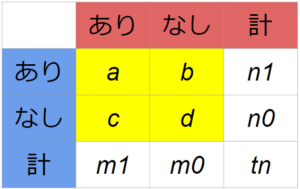
lgorは対数オッズ比、
seは標準誤差、
lowは95%信頼区間下限、
uppは95%信頼区間上限。

詳しくは以下の記事も参照のこと。

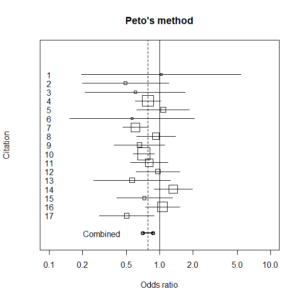
オッズ比は以下のように計算する。

$$ オッズ比 = \frac{ac}{bc} $$

se標準誤差は以下の通りの計算。

$$ se = \sqrt{\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d}} $$

ai <- dat$a
bi <- dat$n1 - dat$a
ci <- dat$c
di <- dat$n0 - dat$c
tn <- dat$n1 + dat$n0
lgor <- log(ai*di/bi/ci)
se <- sqrt(1/ai+1/bi+1/ci+1/di)
low <- exp(lgor-1.96*se)
upp <- exp(lgor+1.96*se)
round(cbind(ORi=exp(lgor), LLi=low, ULi=upp),4)

各試験のオッズ比と95%信頼区間は以下のようになる。

> round(cbind(ORi=exp(lgor), LLi=low, ULi=upp),4)
        ORi    LLi    ULi
[1,] 1.0286 0.1943 5.4454
[2,] 0.4766 0.1849 1.2287
[3,] 0.5824 0.1926 1.7611
[4,] 0.7818 0.5963 1.0250
[5,] 1.0719 0.6184 1.8581
[6,] 0.5576 0.1483 2.0964
[7,] 0.5991 0.4565 0.7862
[8,] 0.9244 0.6197 1.3788
[9,] 0.6543 0.3824 1.1194
[10,] 0.7155 0.5688 0.9000
[11,] 0.8078 0.5514 1.1836
[12,] 0.9618 0.6135 1.5081
[13,] 0.5525 0.2401 1.2713
[14,] 1.3252 0.8859 1.9822
[15,] 0.7252 0.4046 1.2998
[16,] 1.0558 0.7384 1.5096
[17,] 0.4893 0.2671 0.8965

統合オッズ比と95%信頼区間を計算する

漸近分散法でオッズ比を統合する。

q1は均質性の検定統計量。
q2は有意性の検定統計量。

# --------------- fixed effects ---------------
k <- length(ai)
w <- 1/se/se
sw <- sum(w)
varor <- exp(sum(lgor*w)/sw)
varorl <- exp(log(varor)-1.96*sqrt(1/sw))
varoru <- exp(log(varor)+1.96*sqrt(1/sw))
q1 <- sum(w*(lgor-log(varor))^2)
df1 <- k-1
pval1 <- 1-pchisq(q1, df1)
q2 <- log(varor)^2*sw
df2 <- 1
pval2 <- 1-pchisq(q2, df2)
list(round(c(ORv=varor, LL=varorl, UL=varoru, Q1=q1, df1=df1,P1=pval1, Q2=q2, df2=df2, P2=pval2),4))

結果は以下の通り。

オッズ比と95%信頼区間は 0.7831(0.7067 – 0.8677)

均質性q1は有意でなく、均質と言ってよさそう。

有意性q2は統計学的有意。

> list(round(c(ORv=varor, LL=varorl, UL=varoru, Q1=q1, df1=df1,P1=pval1, Q2=q2, df2=df2, P2=pval2),4))
1
   ORv      LL      UL      Q1     df1      P1      Q2     df2      P2
0.7831  0.7067  0.8677 21.4798 16.0000  0.1608 21.8063  1.0000  0.0000

フォレストプロットで眺めてみる

個々の試験をプロットして、統合オッズ比も同時にプロットする。

個々の試験の四角の大きさは、サンプルサイズの平方根で、試験の重み（重要度）を表している。

# ------------- individual graph ----------------
id <- k:1
plot(exp(lgor), id, ylim=c(-3,20),
log="x", xlim=c(0.1,10), yaxt="n", pch="",
ylab="Citation", xlab="Odds ratio")
title(main=" Variance-based method ")
symbols(exp(lgor), id, squares=sqrt(tn),
add=TRUE, inches=0.25)
for (i in 1:k){
j <- k-i+1
x <- c(low[i], upp[i])
y <- c(j, j)
lines(x, y, type="l")
text(0.1, i, j)
}
# -------------- Combined graph --------------
varorx <- c(varorl, varoru)
varory <- c(-1, -1)
lines(varorx, varory, type="o", lty=1, lwd=2)
abline(v=c(varor), lty=2)
abline(v=1)
text(0.2, -1, "Combined:fixed")

フォレストプロットはこちら。

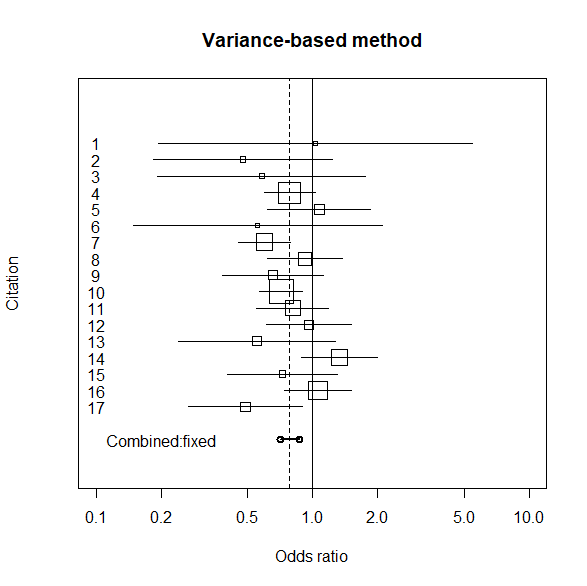
metaforパッケージを使った方法

metaforパッケージのrma.uni()を使うととても簡単できれいにできる。

初回だけインストールする。

install.packages("metafor")

library() 関数で metafor パッケージを呼び出して、以下のように計算する。

library(metafor)
dat.escalc <- escalc(measure="OR", ai=a, n1i=n1, ci=c, n2i=n0, data=dat)
res.fe <- rma.uni(yi, vi, method="FE", data=dat.escalc)

escalc()でestimate（オッズ比推定値）とvariance（分散）を計算する。

escalc()内のmeasureは何を指標にするかということ。

estimateはyi, varianceはviという変数名で計算される。

rma.uni()で漸近分散法の統合オッズ比が計算される。

method=”FE”のFEはFixed Effect（固定効果）の略語。

計算結果は以下の通り。

> res.fe
Fixed-Effects Model (k = 17)
Test for Heterogeneity:
Q(df = 16) = 21.4798, p-val = 0.1608
Model Results:
estimate      se     zval    pval    ci.lb    ci.ub
-0.2445  0.0524  -4.6697  <.0001  -0.3471  -0.1419  ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

estimateとci.lb, ci.ubが対数なので、よくわからない。

exp()して真数に戻そう。

round(exp(c(coef(res.fe), res.fe$ci.lb, res.fe$ci.ub)),4)

metaforパッケージを使わなかった上述の計算結果と同じく、オッズ比と95%信頼区間は 0.7831(0.7067 – 0.8677) となった。

> round(exp(c(coef(res.fe), res.fe$ci.lb, res.fe$ci.ub)),4)
intrcpt
0.7831 0.7067 0.8677

フォレストプロットも一瞬で完成。

forest(res.fe)

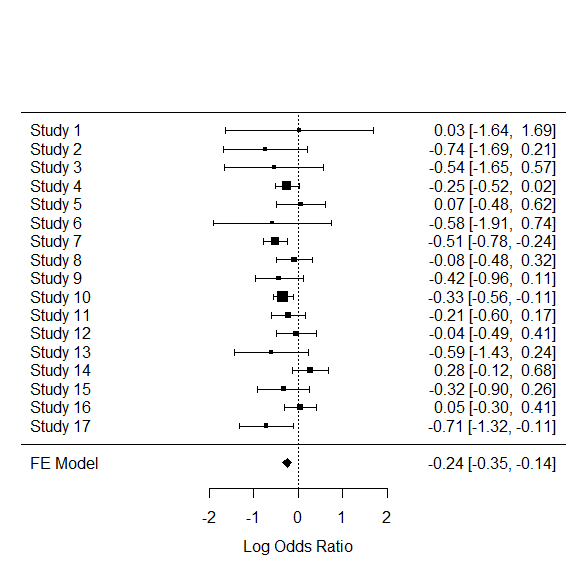
まとめ

漸近分散法でオッズ比を統合してメタアナリシスする方法を解説した。

参考になれば。

参考書籍

丹後俊郎著　メタ・アナリシス入門　朝倉書店
3.1 ２×２分割表　3.1.2 漸近分散法―オッズ比
付録B.4　アルゴリズム3.2 varor.s

新版はこちら