R で 生存時間データに対して、Penalized Spline(罰則付きスプライン)曲線を書く方法の解説
Penalized Spline とは
Penalized Spline(罰則付きスプライン、P スプライン)は、データに合わせた滑らかな曲線を求めるために使われる方法の一つだが、過剰適合(オーバーフィッティング)を防ぐためにペナルティ(罰則)を加える手法
曲線の 2 階微分(曲がり具合)に対してペナルティを課すことで、過度に複雑な形状を避けて、滑らかな推定を行う
自由度の 2 ~ 3 倍のノットを配置すると適切なスムージングが行える(連続データで自由度 1 であれば、2 ~ 3 個のノットという意味)
B スプラインとの違い
スプライン曲線では、B スプラインが知られている
B スプラインもデータを滑らかな曲線にフィットさせる方法だが、過剰適合を防ぐ仕組みがない
Penalized Spline は、データにフィットしつつも、過剰適合を防ぎ、過度に曲がりすぎない曲線を描画する
Penalized Spline を R で書いてみる
suvival パッケージの lung というデータセットを用いて、年齢に対するイベントリスクを Penalized Spline 曲線として書いてみる
スクリプトは以下のとおり
# penalized spline curve
library(survival)
fit <- coxph(Surv(time, status)~pspline(age), data=lung)
termplot(fit, se=TRUE)
abline(h=0)
summary(fit)
coxph 関数内の pspline が Penalized Spline 項である
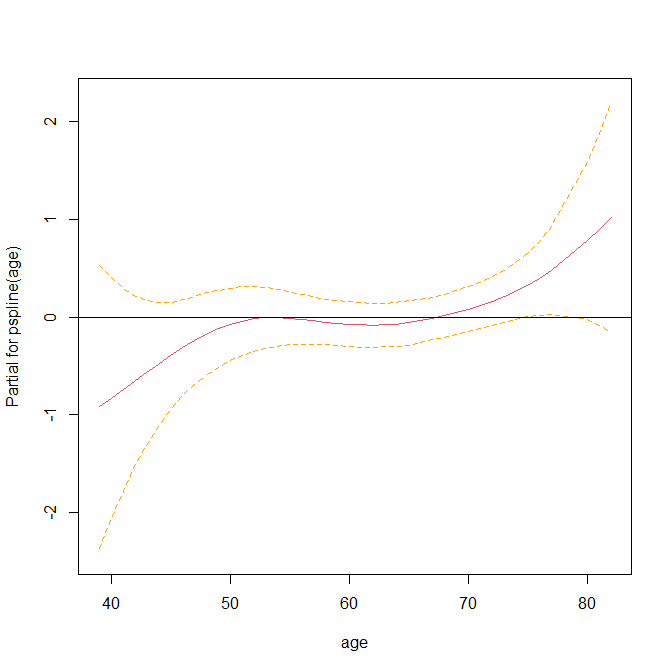
termplot で以下のグラフが書ける
se = TRUE が、信頼区間を表示する引数である
赤い線が点推定値で、オレンジの破線が 95 % 信頼区間である
Y 軸は対数ハザード比である
計算結果は以下のとおり
> summary(fit)
Call:
coxph(formula = Surv(time, status) ~ pspline(age), data = lung)
n= 228, number of events= 165
coef se(coef) se2 Chisq DF p
pspline(age), linear 0.01879 0.009014 0.009014 4.34 1.00 0.037
pspline(age), nonlin 2.91 3.09 0.420
exp(coef) exp(-coef) lower .95 upper .95
ps(age)3 1.458 0.68597 0.3474 6.117
ps(age)4 2.126 0.47029 0.2097 21.564
ps(age)5 3.089 0.32375 0.2128 44.842
ps(age)6 3.713 0.26930 0.2498 55.195
ps(age)7 3.575 0.27969 0.2562 49.897
ps(age)8 3.336 0.29972 0.2454 45.359
ps(age)9 3.371 0.29668 0.2478 45.848
ps(age)10 3.804 0.26289 0.2788 51.900
ps(age)11 4.525 0.22098 0.3298 62.094
ps(age)12 6.031 0.16582 0.4257 85.423
ps(age)13 10.027 0.09973 0.5887 170.793
ps(age)14 17.508 0.05712 0.5730 534.903
Iterations: 4 outer, 11 Newton-Raphson
Theta= 0.8062094
Degrees of freedom for terms= 4.1
Concordance= 0.535 (se = 0.027 )
Likelihood ratio test= 7.74 on 4.09 df, p=0.1linear の部分が 自由度 1 で、nonlinear の部分が自由度 3.09 とわかる
合わせて、Degrees of freedom for terms = 4.1 と理解できる(下から 3 行目)
加えて、以下のように、交絡因子を加えたり、自由度を制御することもできる
# ph.ecog を交絡因子として投入
fit1 <- coxph(Surv(time, status) ~ ph.ecog + pspline(age), lung)
# df (degree of freedom) を 8 に変更(デフォルトは 4)
fit2 <- coxph(Surv(time, status) ~ ph.ecog + pspline(age, 8), lung)
自由度は多くし過ぎず、複雑にしないほうがよく、デフォルトのままでよいように思う
まとめ
以上、R で 生存時間データに対して Penalized Spline 曲線を書く方法をお伝えした
連続データの説明変数に対して、線形にイベントのリスクが上昇しないと想定される場合、過剰適合を避けるためにペナルティがついた Penalized Spline 曲線で、説明変数とイベントとの関係性を描くのが一つの選択肢である
何らか参考になれば








コメント