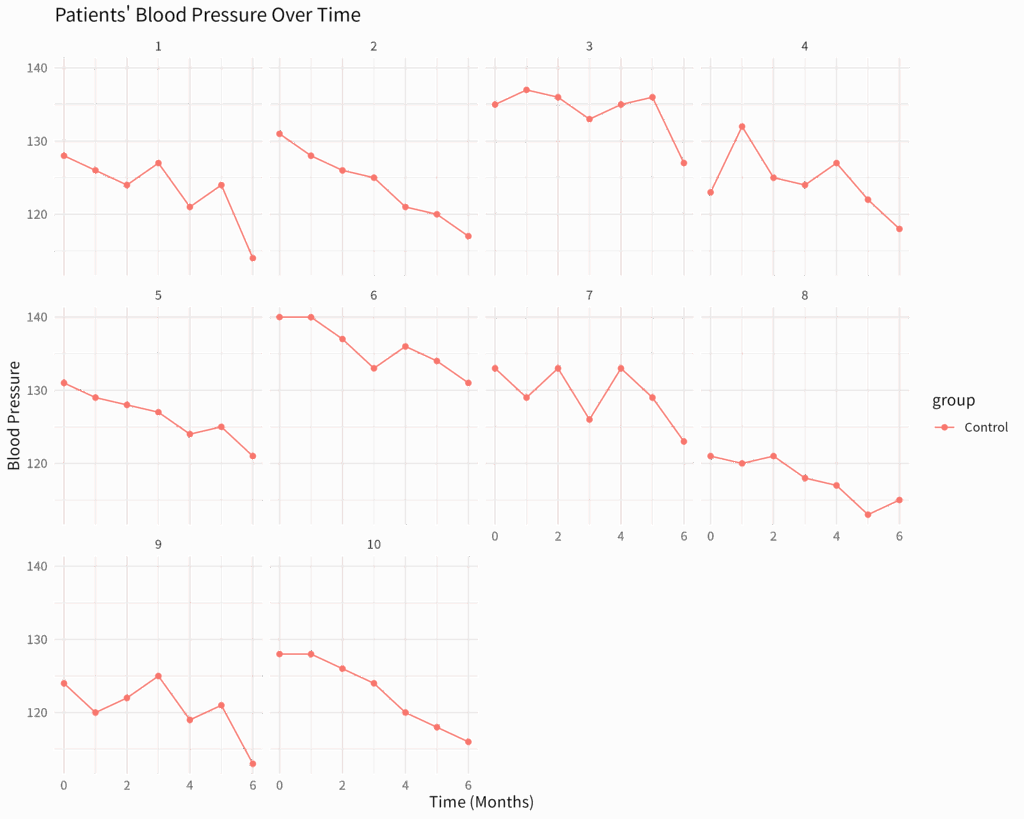2025年– date –
-

多重代入法後のCox回帰:Wald検定(ANOVA)カイ二乗値の統合
多重代入法 (Multiple Imputation, Mice) は、欠損値に対処するための強力な統計的手法である。しかし、多重代入法によって作成された複数のデータセットそれぞれに対して統計解析を行った後、それらの結果をどのように統合すればよいか迷うことがある。本... -

クラスターランダム化比較試験の基礎:研究デザインと適切なサンプルサイズ計算
従来のランダム化比較試験(RCT)は、個々の参加者をランダムにグループに割り付けることで、介入の効果を公平に評価するための強力な手法である。しかし、医療や教育の現場では、個人ではなくグループ(クラスター)単位で介入が行われることが少なくない... -

尺度開発 信頼性・妥当性研究論文リスト
随時追加していく 看護学分野 退院後早期の育児不安尺度の開発と信頼性・妥当性の検討 産後2週間の母親373名を対象とした調査で、育児不安尺度(20項目4因子:負担感、抑うつ気分、母乳不足感、児の哺乳の不安定感)の信頼性・妥当性が確認された。本尺度... -

線形混合効果モデル:反復測定データ解析の強力なツール
臨床研究や生物学研究において、同じ被験者から複数回測定されたデータ(反復測定データ)は頻繁に登場する。このようなデータは、従来の線形回帰モデルでは適切に解析できない場合がある。なぜなら、同じ被験者からの測定値は互いに相関を持つため、独立... -

信頼区間の重なりで「差」を判断してはいけない理由
2つのグループの平均値を比較する際、多くの人がそれぞれの平均値の95%信頼区間が重なっているかどうかを見て、「統計学的に有意な差があるか」を判断しようとする。しかし、これは誤りである。実は、2つの信頼区間が重なっていたとしても、統計学的に有意... -

生物学的同等性試験における90%信頼区間の重要性
新薬開発や後発医薬品(ジェネリック医薬品)の開発において、薬剤の有効性と安全性を科学的に評価することは極めて重要である。その中でも、すでに承認されている医薬品(先発医薬品)と新しい医薬品が、体内で同等に作用するかを評価する生物学的同等性... -

反復測定データの解析:EM平均を用いた群間・時点間比較
臨床研究では、同一の対象者に対して複数回測定を行う反復測定デザインが頻繁に用いられる。このようなデータは、時間経過に伴う変化や介入効果を評価する上で非常に有用だが、一方で、複雑な相関構造をモデル化するという課題がある。この複雑な相関構造... -

固定効果と変量効果:データ解析における「平均」と「個人差」の捉え方
医療研究や社会調査など、さまざまな分野のデータ解析で登場する固定効果と変量効果。これらは、データを回帰モデルで分析する際に、「集団全体の平均的な傾向」と「個々の対象が持つ固有のばらつき」をどのように扱うか、という考え方に基づいている。 固... -

一般化推定方程式(GEE)の基礎と臨床研究での応用
臨床研究や疫学研究において、繰り返し測定されるデータやクラスター化されたデータは頻繁に登場する。このようなデータでは、同じ被験者からの測定値や同じクラスター内の観測値には相関があるため、従来の独立性を仮定する統計手法では適切な解析ができ... -

一般化線形混合モデル(GLMM)の基本と応用
臨床研究や生物統計学の分野では、患者ごとのばらつきや測定の反復性など、データが持つ複雑な構造を考慮することが不可欠である。しかし、基礎的な統計モデルでは、このような複雑性を十分に捉えきれない。そこで必要となってくるのが、「一般化線形混合... -

同等性検定と必要サンプル数計算:臨床研究における実践的アプローチ
新しい治療法が既存のものと同等であることを証明したい。そんな時、従来の「優れているか」を問う研究だけでは不十分である。本記事では、臨床現場で役立つ同等性検定の基本から、医師が直面する具体的なケースでの活用法、そして研究の成功に不可欠な必... -

統計的推測のその先へ:効果量の計算と実践
研究論文や統計解析の結果を目にしたとき、「有意差があった」という報告に接する機会は多い。しかし、P値が示す統計的有意性は、あくまで偶然によるものか否かという確率的な指標に過ぎない。では、その研究によって「どれくらいの効果があったのか」「そ... -

効果量とサンプルサイズの関係性:統計的検出力の向上を目指して
統計的仮説検定は、日々直面する様々な疑問に科学的に答えを出すための強力なツールである。特に医療や教育といった分野では、新しい治療法や学習方法の効果を検証する際に不可欠である。この検証の鍵を握るのが「効果量」と「サンプルサイズ」。これら二... -

有意水準、検出力、サンプルサイズ:統計的仮説検定の三位一体
統計的仮説検定は、科学研究やビジネスにおいて意思決定を行う上で不可欠なツールである。しかし、その結果を正しく解釈し、適切な結論を導き出すためには、「有意水準」「検出力」「サンプルサイズ」という三つの重要な概念の相互関係を理解することが不... -

R で感度・特異度分析に必要なサンプル数を計算する方法
診断検査の感度・特異度分析におけるサンプルサイズ計算は、研究の目的、疾患有病率、期待される感度・特異度、許容誤差、検出力に基づいて行われる。小さすぎると信頼性が低く、大きすぎるとリソースが無駄になる。統計的に信頼できる結果を得るには、こ... -

R で適合度の検定に必要なサンプル数を計算する方法
「あなたのデータ、本当にその仮説に合ってる?」📈 統計分析でよくあるこの疑問。 今回は、観測されたデータが、ある理論的な分布や比率にどれくらい「適合しているか」を科学的に評価する「適合度検定」について、基本から具体例、必要なサンプル... -

R でマクネマー検定に必要なサンプル数を計算する方法
「治療前後の効果」「施策による意識の変化」など、同じ対象者の2つの時点での変化を知りたいとき、マクネマー検定が役立つ。この検定は2値データ(はい/いいえなど)の変化を分析するのに最適。 この記事では、マクネマー検定の基本から、Rを使った計算例... -

傾向スコア法でバランスが取れないときの対処法
バランスが取れないときの対処法 共変量を見直す 傾向スコア作成のための共変量は、アウトカムに関連があり、要因にも関連があるものが候補である だが、要因にしか関連ないものは、除くとよい その観点で見直すと良い 参考:傾向スコア作成の際の変数の選... -

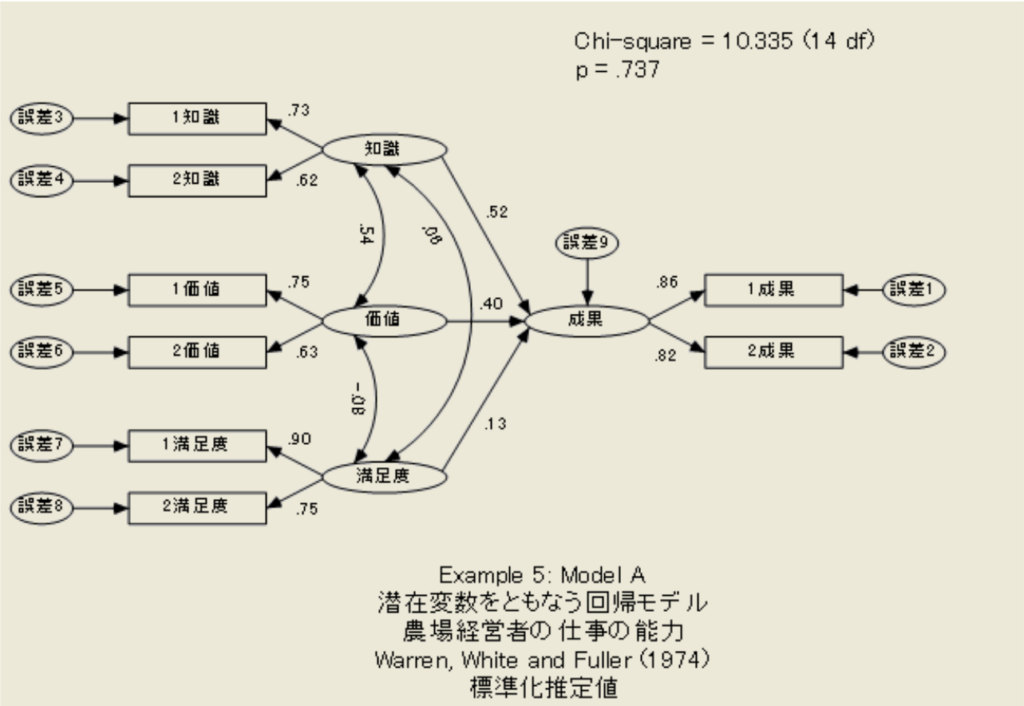
共分散構造分析の例と参考書籍
共分散構造分析は、構造方程式モデリング SEM とも呼ばれる、変数間の相関を元に、想定する概念モデルにデータが当てはまっているか、変数同士の関連性は強いのか弱いのか、ということを検討する手法である 具体的な事例が掲載されている論文および実践す... -

EZR と R を使って中央値に最小値・最大値のエラーバーがついた折れ線グラフを書く方法
反復測定データの各時点の中央値及び最小値・最大値を示したエラーバーがついた折れ線グラフを書きたいという要望はよく聞くが、そのようなグラフを書けるソフトウェアはなかなか見つからない EZR と R で中央値に最小値・最大値エラーバー付きの折れ線グ...
12