ギブスサンプリング(ギブス法)を R で実施する方法。
初期値を与えて、何度もサンプリングしていると、だんだんに形になってくる。
目次
ギブスサンプリング用のデータの用意
heikinという名前のデータを入力する。
heikin <- c(6.0,10.0,7.6,3.5,1.4,2.5,5.6,3.0,2.2,5.0,
3.3,7.6,5.8,6.7,2.8,4.8,6.3,5.3,5.4,3.3,
3.4,3.8,3.3,5.7,6.3,8.4,4.6,2.8,7.9,8.9)
mean1 <- mean(heikin)
n <- length(heikin)
mean(heikin)
var(heikin)
heikinデータの平均、分散、サンプルサイズは、以下の通り。
> mean(heikin)
[1] 5.106667
> var(heikin)
[1] 4.766161
> length(heikin)
[1] 30
ギブスサンプリングを行うためのパッケージをインストールする
psclパッケージをインストールする。一回だけ。
install.packages("pscl")
psclパッケージを、呼び出す。
library(pscl)
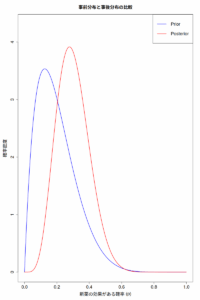
ギブスサンプリングの事前分布の図示
0.05から10まで、0.05刻みの変数xを作る。
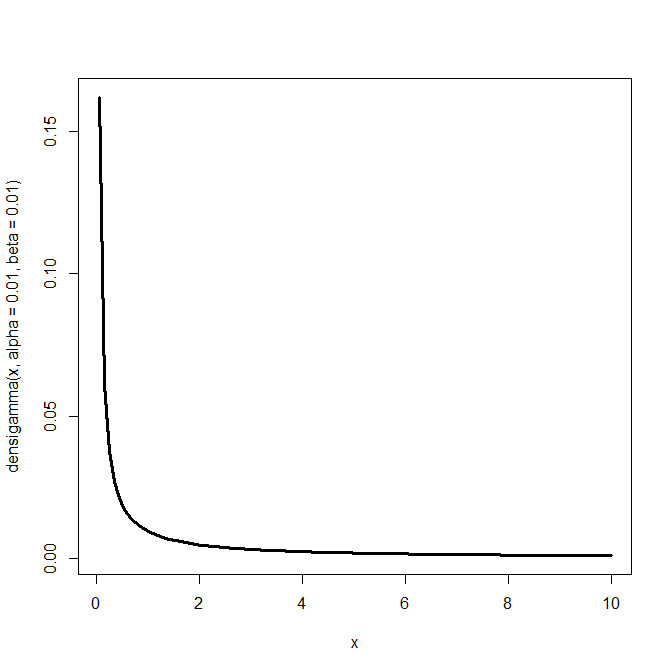
alpha=0.01, beta=0.01の逆ガンマ分布を描く。
これが事前分布。
x <- seq(0.05,10,0.05)
curve(densigamma(x,alpha=0.01, beta=0.01),from=0.05,to=10,lwd=3)
ギブスサンプリングのための条件設定
ここで条件設定。
n0 <- 2*0.01
n0S0 <- 2*0.01
S0 <- n0S0/n0
mu0 <- 5
m0 <- 1/4
m1 <- m0+n
n1 <- n0+n
mu1 <- (n*mean1+m0*mu0)/(m0+n)
Q <- sum((heikin-mean1)^2)
n1S1 <- n0S0+Q+m0*n/(m0+n)*(mean1-mu0)^2
サンプリングのための関数を準備する
分散の事後分布から母分散 $ \sigma^2 $ をサンプリングする関数。
my.sigma2 <- function(mu){
sigma2 <- rigamma(1, alpha=(n1+1)/2, beta=(n1S1+m1*(mu-mu1)^2)/2)
return(sigma2)
}
平均の事後分布から母平均をサンプリングする関数。
my.mu <- function(sigma2){
mu <- rnorm(1, mean=mu1, sd=sqrt(sigma2/m1))
return(mu)
}
モンテカルロ法によるシミュレーション
モンテカルロ シミュレーションを実行する。
my.montecarlo <- function(n){
set.seed(20110608)
mu <- 5
new.mu <- 5
sigma2 <- 4
for (i in 1:n){
new.sigma2 <- my.sigma2(new.mu)
sigma2 <- sigma2 + new.sigma2
new.mu <- my.mu(new.sigma2)
mu <- mu + new.mu
}
list("mu"=mu/n, "sigma2"=sigma2/n)
}
10万回サンプリングした結果は以下の通り。
> my.montecarlo(100000)
$`mu`
[1] 5.102863
$sigma2
[1] 4.936363
ギブスサンプリングで得られた事後分布の図示
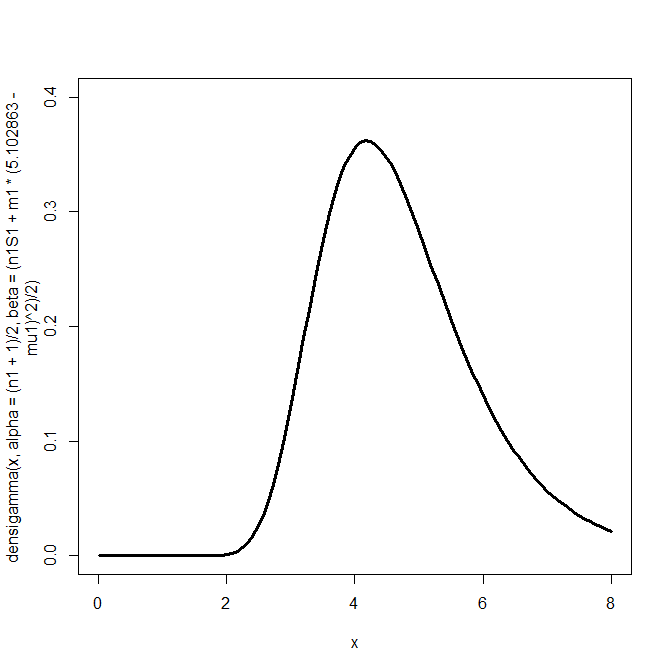
分散の事後分布を描いてみる。
curve(densigamma(x, alpha=(n1+1)/2, beta=(n1S1+m1*(5.102863-mu1)^2)/2),from=0.01,to=8.0, ylim=c(0,0.4),lwd=3)
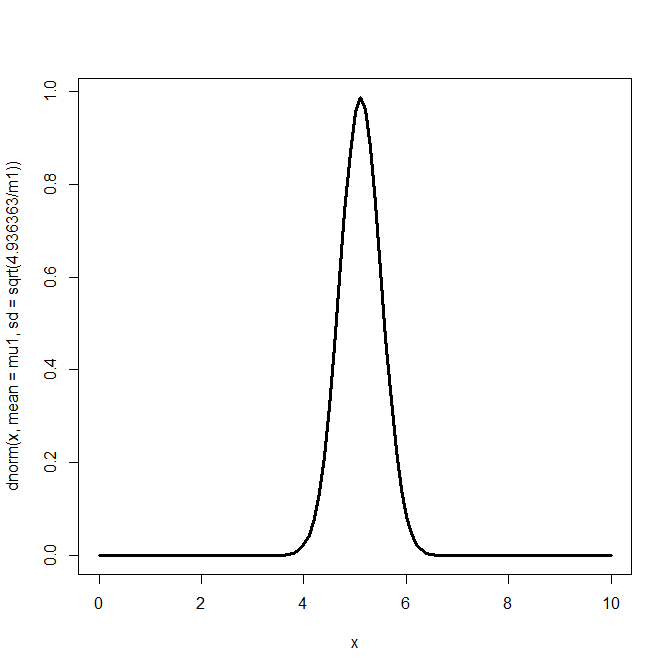
サンプリング結果を使って平均の分布を描いてみる。
curve(dnorm(x, mean=mu1, sd=sqrt(4.936363/m1)),from=0,to=10,lwd=3)
まとめ
ギブスサンプリングを参考書籍通りに R で行ってみた。
参考書籍







コメント