複数の研究結果を統合し、より強固なエビデンスを導き出すメタアナリシスは、医療や心理学、社会科学など多岐にわたる分野で重要な役割を果たしている。しかし、従来の頻度論的アプローチでは扱いにくい問題や、事前情報の活用といった点で限界があった。そこで近年注目されているのが、ベイズの定理を用いたメタアナリシスである。本記事では、ベイズメタアナリシスの概要から、そのメリット、具体的な計算例、そして結果の解釈までを分かりやすく解説する。
ベイズの定理を用いたメタアナリシスの概要
ベイズの定理を用いたメタアナリシスは、従来の頻度論的アプローチとは異なり、不確実性を確率分布として表現し、事前情報(事前分布)とデータ(尤度)を組み合わせることで事後情報(事後分布)を導き出す点が特徴だ。これにより、研究間の異質性やサンプルサイズの小ささといった課題に柔軟に対応し、より包括的な推論を可能にする。
主な手法としては、以下のものが挙げられる。
- ベイズメタアナリシス(Bayesian Meta-Analysis): 複数の研究から得られた効果量を統合し、共通の効果量や研究間の異質性の程度を推定する。個々の研究の結果を条件付きでモデル化し、統合された効果量の事後分布を導き出す。
- ベイジアンメタ回帰(Bayesian Meta-Regression): メタアナリシスに回帰分析の要素を導入したもので、研究間の異質性を説明する共変量(例:治療期間、患者の年齢層、出版年など)の効果を評価する。これにより、なぜ研究間で結果が異なるのかを統計的に探ることが可能となる。
ベイズメタアナリシスの使い所
ベイズメタアナリシスは、特に以下のような場面でその真価を発揮する。
- 事前情報を活用したい場合: 過去の研究結果や専門家の知見など、分析に利用できる事前情報がある場合に、それをモデルに組み込むことでより精度の高い推定が可能となる。
- サンプルサイズが小さい研究が多い場合: 個々の研究のサンプルサイズが小さい場合でも、事前情報を活用したり、MCMC(マルコフ連鎖モンテカルロ法)などのシミュレーションによって、安定した推定を行うことができる。
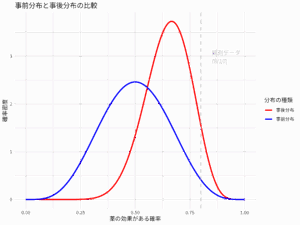
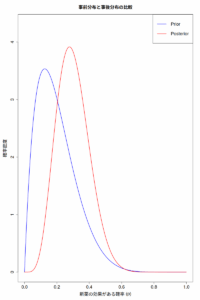
- 不確実性を明示的に表現したい場合: 推定される効果量が点推定ではなく、確率分布として得られるため、その不確実性を視覚的に理解しやすくなる。
- 研究間の異質性をより詳細に検討したい場合: ベイジアンメタ回帰を用いることで、異質性の原因となる要因を探索的に分析できる。
- エビデンスの累積的な統合: 新しい研究結果が得られるたびに、既存の事後分布を事前分布として更新していくことで、エビデンスを継続的に統合し、リアルタイムでの意思決定に役立てることができる。
具体例と R 計算例
ここでは、簡単な具体例として、複数の研究から得られた二値変数のオッズ比を統合するベイズメタアナリシスのRでの計算例を示す。今回はBayesmetaパッケージを使ったアプローチに加え、ベイジアンメタ回帰の例も示す。
例1:ある治療法の効果に関する複数の臨床試験のオッズ比の統合(Bayesmetaパッケージを使用)
架空の研究データ:
| 研究ID | オッズ比 (OR) | 95%信頼区間下限 | 95%信頼区間上限 |
| 1 | 1.5 | 0.8 | 2.8 |
| 2 | 2.0 | 1.2 | 3.3 |
| 3 | 1.3 | 0.7 | 2.4 |
| 4 | 1.8 | 1.0 | 3.2 |
これらのオッズ比の対数(log OR)とその標準誤差(SE)を計算する。
$\log(\text{OR})$の標準誤差は、
$$\frac{\log(\text{上限}) – \log(\text{下限})}{2 \times 1.96}$$
で近似できる。
R スクリプト例:
# bayesmetaパッケージのインストールと読み込み(初回のみ)
# install.packages("bayesmeta")
library(bayesmeta)
# データの準備 (架空のデータ)
study_id <- c(1, 2, 3, 4)
or <- c(1.5, 2.0, 1.3, 1.8)
lower_ci <- c(0.8, 1.2, 0.7, 1.0)
upper_ci <- c(2.8, 3.3, 2.4, 3.2)
# 対数オッズ比と標準誤差の計算
log_or <- log(or)
se_log_or <- (log(upper_ci) - log(lower_ci)) / (2 * 1.96)
# bayesmetaパッケージを使ったメタアナリシス
# y: 効果量 (log_or)
# sigma: 効果量の標準誤差 (se_log_or)
bm_result <- bayesmeta(y=log_or, sigma=se_log_or)
# 結果のサマリー表示
summary(bm_result)実行結果:
> # 結果のサマリー表示
> summary(bm_result)
'bayesmeta' object.
data (4 estimates):
y sigma
01 0.4054651 0.3195824
02 0.6931472 0.2580615
03 0.2623643 0.3143224
04 0.5877867 0.2967221
tau prior (improper):
uniform(min=0, max=Inf)
mu prior (improper):
uniform(min=-Inf, max=Inf)
ML and MAP estimates:
tau mu
ML joint 0 0.5122391
ML marginal 0 0.5071712
MAP joint 0 0.5122413
MAP marginal 0 0.5072305
marginal posterior summary:
tau mu theta
mode 0.0000000 0.50723049 0.5097047
median 0.2150901 0.50456349 0.5061422
mean 0.3679468 0.50200263 0.5020026
sd NA 0.39345130 0.8284503
95% lower 0.0000000 -0.07962523 -0.6943959
95% upper 1.1116819 1.07026688 1.6802258
(quoted intervals are shortest credible intervals.)
relative heterogeneity I^2 (posterior median): 0.3462448
> Bayesmetaパッケージは、主要な事前分布(一様分布など)を簡単に指定でき、MCMCサンプリングなどを意識せずに結果を得られるため、初心者にも扱いやすい。summary(bm_result)で、統合効果量(mu)と異質性(tau)の事後平均、中央値、信用区間などがまとめて表示される。
ベイズメタアナリシス結果解釈
1. データ概要
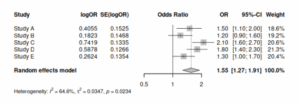
- 4つの研究が含まれており、各研究のオッズ比(OR)は1.3〜2.0の範囲
- 対数オッズ比に変換して分析が行われている
2. 事前分布の設定
- τ(異質性)の事前分布: 一様分布(0〜∞)- 非情報的事前分布
- μ(全体効果量)の事前分布: 一様分布(-∞〜∞)- 非情報的事前分布
3. 主要な結果
全体効果量(μ)
- 事後平均: 0.502(対数スケール)
- 事後中央値: 0.505
- 95%信用区間: -0.080 〜 1.070
- 標準偏差: 0.393
解釈: 対数オッズ比0.502は、元のスケールでは約1.65のオッズ比に相当する。95%信用区間が0を含んでいるので、統計的に有意な効果があるとは言えない結果である。
異質性(τ)
- 事後平均: 0.368
- 事後中央値: 0.215
- 95%信用区間: 0.000 〜 1.112
- I²統計量: 34.6%
解釈:
- 異質性は中程度(I² = 34.6%)
- 95%信用区間の下限が0であるため、研究間の異質性が統計的に有意とは言えない
- しかし、上限が1.112と比較的大きいため、異質性の可能性は残っている
4. 統計的推定量の比較
- ML(最尤)推定: τ = 0, μ = 0.507
- MAP(最大事後確率)推定: τ = 0, μ = 0.507
両方の推定値が非常に近い値となっており、推定の安定性を示している。
5. 実用的な解釈
- 効果の方向性: 介入は正の効果を示している(オッズ比 > 1)
- 研究間の一貫性: 中程度の異質性があるが、統計的に有意ではない
- 実用性: 95%信用区間が実用的な範囲内にあるため、臨床的に意味のある効果の可能性がある
この結果は、介入の有効性を示唆していますが、研究間の異質性についてはさらなる検討が必要かもしれない。
例2:治療期間が効果に与える影響を分析するベイジアンメタ回帰
ベイジアンメタ回帰については、Bayesmetaパッケージ単体では直接的な機能は提供されていない。これは、Bayesmetaが主に共通の効果量と異質性の推定に焦点を当てているためだ。メタ回帰のような複雑なモデルを構築するには、rstanやbrmsのようなより汎用的なベイズ統計モデリングパッケージを使用する必要がある。
以下に、brmsパッケージを使ったベイジアンメタ回帰の例を示す。brmsはStanをバックエンドとして利用し、非常に柔軟なベイズモデルを記述できるため、複雑なメタ回帰モデルにも対応可能だ。
架空の研究データに「治療期間(月)」を追加する。
| 研究ID | オッズ比 (OR) | 95%信頼区間下限 | 95%信頼区間上限 | 治療期間 (月) |
| 1 | 1.5 | 0.8 | 2.8 | 3 |
| 2 | 2.0 | 1.2 | 3.3 | 6 |
| 3 | 1.3 | 0.7 | 2.4 | 2 |
| 4 | 1.8 | 1.0 | 3.2 | 5 |
| 5 | 2.5 | 1.5 | 4.0 | 7 |
| 6 | 1.2 | 0.6 | 2.3 | 4 |
R スクリプト例:
# brmsパッケージのインストールと読み込み(初回のみ)
# install.packages("brms")
library(brms)
# データの準備 (架空のデータに治療期間を追加)
study_id_mr <- c(1, 2, 3, 4, 5, 6)
or_mr <- c(1.5, 2.0, 1.3, 1.8, 2.5, 1.2)
lower_ci_mr <- c(0.8, 1.2, 0.7, 1.0, 1.5, 0.6)
upper_ci_mr <- c(2.8, 3.3, 2.4, 3.2, 4.0, 2.3)
duration_mr <- c(3, 6, 2, 5, 7, 4) # 治療期間 (月)
# 対数オッズ比と標準誤差の計算
log_or_mr <- log(or_mr)
se_log_or_mr <- (log(upper_ci_mr) - log(lower_ci_mr)) / (2 * 1.96)
# データフレームの作成
data_meta_regression <- data.frame(study_id_mr, log_or_mr, se_log_or_mr, duration_mr)
print(data_meta_regression)
# brmsを使ったベイジアンメタ回帰モデル
# formula: log_or_mr | se(se_log_or_mr) は「log_or_mrを、標準誤差se_log_or_mrを考慮してモデル化する」を意味する
# ~ duration_mr + (1 | study_id_mr) は「治療期間を固定効果、研究IDをランダム効果としてモデルに含める」を意味する
# family: gaussian は正規分布に従うことを示す。効果量が対数オッズ比なので適切。
# prior: 事前分布を指定。ここではデフォルト(非情報的な事前分布)を使用しているが、必要に応じて調整できる。
# iter, chains: MCMCサンプリングの反復回数とチェーン数
# silent: true でサンプリング中のメッセージを非表示にする
brm_model_mr <- brm(log_or_mr | se(se_log_or_mr) ~ duration_mr + (1 | study_id_mr),
data = data_meta_regression,
family = gaussian(),
prior = prior(normal(0, 10), class = b), # 回帰係数の事前分布
iter = 2000, chains = 4, silent = TRUE)
#
# # 結果のサマリー
summary(brm_model_mr)実行結果:
> # # 結果のサマリー
> summary(brm_model_mr)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: log_or_mr | se(se_log_or_mr) ~ duration_mr + (1 | study_id_mr)
Data: data_meta_regression (Number of observations: 6)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Multilevel Hyperparameters:
~study_id_mr (Number of levels: 6)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.19 0.18 0.01 0.67 1.00 1435 1260
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept -0.09 0.45 -0.97 0.78 1.00 1926 1340
duration_mr 0.13 0.09 -0.04 0.31 1.00 1952 1404
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.00 0.00 0.00 0.00 NA NA NA
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
警告メッセージ:
There were 2 divergent transitions after warmup. Increasing adapt_delta above 0.8 may help. See http://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
>
>
> # # 結果のサマリー
> summary(brm_model_mr)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: log_or_mr | se(se_log_or_mr) ~ duration_mr + (1 | study_id_mr)
Data: data_meta_regression (Number of observations: 6)
Draws: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup draws = 4000
Multilevel Hyperparameters:
~study_id_mr (Number of levels: 6)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sd(Intercept) 0.19 0.20 0.00 0.71 1.00 895 840
Regression Coefficients:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
Intercept -0.08 0.49 -1.07 0.82 1.00 1757 1414
duration_mr 0.13 0.10 -0.04 0.33 1.00 1787 1342
Further Distributional Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.00 0.00 0.00 0.00 NA NA NA
Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
> ベイジアンメタ回帰分析結果の解釈
1. モデル概要
- 分析対象: 6つの研究
- 従属変数: 対数オッズ比(log_or_mr)
- 独立変数: 治療期間(duration_mr、月単位)
- モデル構造: 階層的線形モデル(研究IDをランダム効果として含む)
2. 主要な結果
固定効果(Population-Level Effects)
切片(Intercept)
- 推定値: -0.09
- 標準誤差: 0.45
- 95%信用区間: -0.97 〜 0.78
治療期間の効果(duration_mr)
- 推定値: 0.13
- 標準誤差: 0.09
- 95%信用区間: -0.04 〜 0.31
ランダム効果(Multilevel Hyperparameters)
研究間の標準偏差(sd(Intercept))
- 推定値: 0.19
- 標準誤差: 0.18
- 95%信用区間: 0.01 〜 0.67
3. 結果の解釈
治療期間の効果について
- 正の係数(0.13): 治療期間が長くなるほど、対数オッズ比が増加する傾向
- 95%信用区間: -0.04 〜 0.31(0を含む)
- 解釈: 治療期間の効果は統計的に有意ではない(p > 0.05相当)
実用的な意味
- 治療期間が1ヶ月増加するごとに、対数オッズ比が平均0.13増加
- 元のスケールでは、治療期間が1ヶ月増加するごとに、オッズ比が約1.14倍($e^{0.13}$)増加する傾向
- しかし、この効果は統計的に確実ではない
研究間の異質性
- 標準偏差: 0.19 研究間で中程度の異質性が存在
- 95%信用区間: 0.01 〜 0.67(下限が0に近い)
- 解釈: 研究間の異質性は比較的小さいが、存在する可能性がある
4. モデルの診断
収束性
- Rhat値: すべて1.00(良好な収束)
- Effective Sample Size: 十分なサンプルサイズ
- 警告: 2つの発散遷移が発生(adapt_deltaの調整が必要な可能性)
モデルの適合度
- sigma: 0.00(測定誤差が既に標準誤差として考慮されているため)
5. 実用的な結論
- 治療期間の効果: 治療期間が長いほど効果が大きくなる傾向があるが、統計的に確実ではない
- 臨床的意義: 治療期間の延長による効果増加の可能性は示唆されるが、さらなる研究が必要
- 研究間の一貫性: 比較的良好な一貫性を示している
- 推奨事項:
- より多くの研究での検証が必要
- 治療期間の最適化についてのさらなる検討が推奨される
この結果は、治療期間と効果量の関係についての予備的な知見を提供しているが、統計的な確実性は限定的である。
修正されたベイジアンメタ回帰分析結果の解釈
1. モデル診断の改善
- 発散遷移: 警告メッセージが解消され、MCMCサンプリングが安定化
- adapt_delta=0.995: より保守的なサンプリング設定により、収束性が向上
2. 主要な結果(修正版)
固定効果(Population-Level Effects)
切片(Intercept)
- 推定値: -0.08
- 標準誤差: 0.49
- 95%信用区間: -1.07 〜 0.82
治療期間の効果(duration_mr)
- 推定値: 0.13
- 標準誤差: 0.10
- 95%信用区間: -0.04 〜 0.33
ランダム効果(Multilevel Hyperparameters)
研究間の標準偏差(sd(Intercept))
- 推定値: 0.19
- 標準誤差: 0.20
- 95%信用区間: 0.00 〜 0.71
3. 修正された結果の解釈
治療期間の効果について
- 正の係数(0.13): 治療期間が長くなるほど、対数オッズ比が増加する傾向
- 95%信用区間: -0.04 〜 0.33(0を含む)
- 解釈: 治療期間の効果は統計的に有意ではないが、正の傾向は維持
実用的な意味
- 治療期間が1ヶ月増加するごとに、対数オッズ比が平均0.13増加
- 元のスケールでは、治療期間が1ヶ月増加するごとに、オッズ比が約1.14倍($e^{0.13}$)増加する傾向
- 信用区間の上限(0.33)は、最大で1.39倍($e^{0.33}$)の効果増加の可能性を示唆
研究間の異質性
- 標準偏差: 0.19 研究間で中程度の異質性が存在
- 95%信用区間: 0.00 〜 0.71(下限が0に近い)
- 解釈: 研究間の異質性は比較的小さいが、存在する可能性がある
4. モデルの診断(改善後)
収束性
- Rhat値: すべて1.00(良好な収束)
- Effective Sample Size: 十分なサンプルサイズ
- 発散遷移: 解消され、安定したサンプリング
モデルの適合度
- sigma: 0.00(測定誤差が既に標準誤差として考慮されているため)
5. 修正された実用的な結論
- 治療期間の効果:
- 治療期間が長いほど効果が大きくなる傾向がある
- 統計的に確実ではないが、臨床的に意味のある効果の可能性がある
- 最大で約39%の効果増加の可能性
- 臨床的意義:
- 治療期間の延長による効果増加の可能性は示唆される
- 個別の患者や疾患に応じた治療期間の最適化が重要
- 研究間の一貫性:
- 比較的良好な一貫性を示している
- 異質性は存在するが、管理可能な範囲内
- 推奨事項:
- より多くの研究での検証が必要
- 治療期間の最適化についてのさらなる検討が推奨される
- 個別化医療の観点からの治療期間の調整を検討
6. 改善点
- MCMCサンプリングの安定性: adapt_deltaの調整により、より信頼性の高い推定が可能
- 結果の一貫性: 警告なしで安定した結果が得られた
- 解釈の信頼性: 発散遷移がないため、結果の解釈により自信を持てる
この修正された結果は、治療期間と効果量の関係についてより信頼性の高い知見を提供している。
まとめ
ベイズの定理を用いたメタアナリシスは、従来の頻度論的アプローチの限界を克服し、より柔軟で包括的なエビデンス統合を可能にする強力なツールである。事前情報の活用、不確実性の明示的な表現、そして直感的な解釈は、研究者や意思決定者にとって大きなメリットとなる。特に、個別研究のサンプルサイズが小さい場合や、研究間の異質性の原因を探るベイジアンメタ回帰のような応用は、その有用性をさらに高める。
Bayesmetaパッケージを使えば、比較的シンプルなベイズメタアナリシスを簡潔に実行できる。一方、rstanやbrmsといった強力なパッケージを使えば、ベイジアンメタ回帰のようなより複雑なモデルを柔軟に構築し、MCMCサンプリングによる詳細な事後分布を得ることができる。ベイズ統計学の学習コストはあるものの、これらのパッケージの登場により、以前よりも手軽に実践できるようになった。ぜひこの機会に、ベイズメタアナリシスの世界に触れて、データからより深い洞察を得る挑戦をしてみてほしい。






コメント