「データから何かを学ぶ」とき、私たちは常に何らかの「信念」を持っている。ベイズ統計学は、この「信念」をデータに基づいて更新していくという、非常に人間らしい思考プロセスを数学的に表現したものだ。今回は、その中心となる「事前分布」と「事後分布」について、分かりやすい比喩を交えながら解説していく。
ベイズ統計の概略
まず、ベイズ統計学がどのようなものか、簡単に見ていこう。従来の統計学(頻度論統計学)が「データが与えられたとき、それがどのくらい珍しいか」という視点に立つことが多いのに対し、ベイズ統計学は「私たちが持っている知識(事前知識)をデータで更新していく」という考え方をする。
事前分布と事後分布の概略
ベイズ統計学を理解する上で、最も重要な概念が「事前分布」と「事後分布」だ。
- 事前分布(Prior Distribution): データを見る「前」に、私たちが持っている「世界のあり方」に対する信念や知識を表す。これは、過去の経験、専門家の意見、あるいは単なる直感などに基づいているかもしれない。
- 事後分布(Posterior Distribution): データを「見た後」に、そのデータによって更新された「世界のあり方」に対する信念や知識を表す。事前分布にデータからの情報が加わることで、より洗練された、確信度の高い分布になる。
事前分布と事後分布のイメージ
事前分布:宝探し前の「漠然とした期待」
あなたは宝探しに出かける。まだ宝の地図を見ていない段階で、「この島には宝があるらしい」という漠然とした情報や期待を持っているとしよう。もしかしたら、「この島のどこかに隠されているだろう」という漠然とした考えかもしれないし、「昔の噂では、この洞窟の奥にある可能性が高い」という具体的な推測かもしれない。これが事前分布だ。データ(宝の地図や目撃情報)を得る前に、宝の場所(知りたい真実)に対して持っている、あなたの最初の「当たり」のことだ。
事後分布:地図を手に入れて確信に変わる「期待」
いよいよ宝の地図を手に入れた!そこには「古い大木の根元」というヒントが書かれている。あなたは漠然とした期待から一転して、「宝は大木の根元にある!」という強い確信を得るだろう。これが事後分布だ。データ(宝の地図)によって、あなたの宝の場所に対する「信念」が更新され、より具体的な場所を指し示すようになった状態だ。
つまり、ベイズ統計学では、「漠然とした期待(事前分布)」に「具体的な情報(データ)」が加わることで、「確信(事後分布)」へと変化していくプロセスを数学的に記述しているのだ。
具体例と簡単な R での可視化
例:新しい薬の効果
ある新しい薬の効果について考えてみよう。あなたは薬学の専門家として、これまでの経験から「この種類の薬は、だいたい30%から70%くらいの患者に効果があることが多い(平均 0.5 で幅がある)」という事前知識を持っていたとしよう。これは、薬の有効性に対するあなたの事前分布だ。
ここで、実際にこの新しい薬を10人の患者に投与し、8人に効果があったというデータが得られた。
このデータとあなたの事前知識を組み合わせることで、薬の本当の有効性がどのくらいなのか、より正確な情報を得ることができる。
R での簡単な可視化
ここでは、架空のデータを用いて、事前分布と事後分布がどのように変化するかをRでシミュレーションし、可視化してみよう。
R スクリプト例:
# 必要なライブラリをロード (インストールされていない場合は install.packages("ggplot2") でインストール)
library(ggplot2)
# パラメータ設定
# 事前分布のパラメータ (ベータ分布を使用)
# 例えば、事前知識として「効果がある確率は中央値が0.5くらい、幅がそこそこある」と設定
alpha_prior <- 5
beta_prior <- 5
# データの観測 (10人中8人に効果があった)
successes <- 8
trials <- 10
# 事後分布のパラメータ
alpha_posterior <- alpha_prior + successes
beta_posterior <- beta_prior + (trials - successes)
# 確率の範囲
p <- seq(0, 1, length.out = 500)
# 事前分布の確率密度
prior_density <- dbeta(p, alpha_prior, beta_prior)
# 事後分布の確率密度
posterior_density <- dbeta(p, alpha_posterior, beta_posterior)
# データフレームの作成
df <- data.frame(
p = rep(p, 2),
density = c(prior_density, posterior_density),
type = c(rep("事前分布", length(p)), rep("事後分布", length(p)))
)
# 可視化
ggplot(df, aes(x = p, y = density, color = type)) +
geom_line(linewidth = 1.2) +
labs(
title = "事前分布と事後分布の比較",
x = "薬の効果がある確率",
y = "確率密度",
color = "分布の種類"
) +
theme_minimal() +
scale_color_manual(values = c("事前分布" = "blue", "事後分布" = "red")) +
geom_vline(xintercept = successes / trials, linetype = "dashed", color = "gray", linewidth = 0.8) +
annotate("text",
x = successes / trials + 0.05, y = max(posterior_density) * 0.8,
label = paste0("観測データ\n(", successes, "/", trials, ")"), color = "gray", hjust = 0
)
ggsave("Bayes_prior_posterior_distribution.png", width = 8, height = 6)
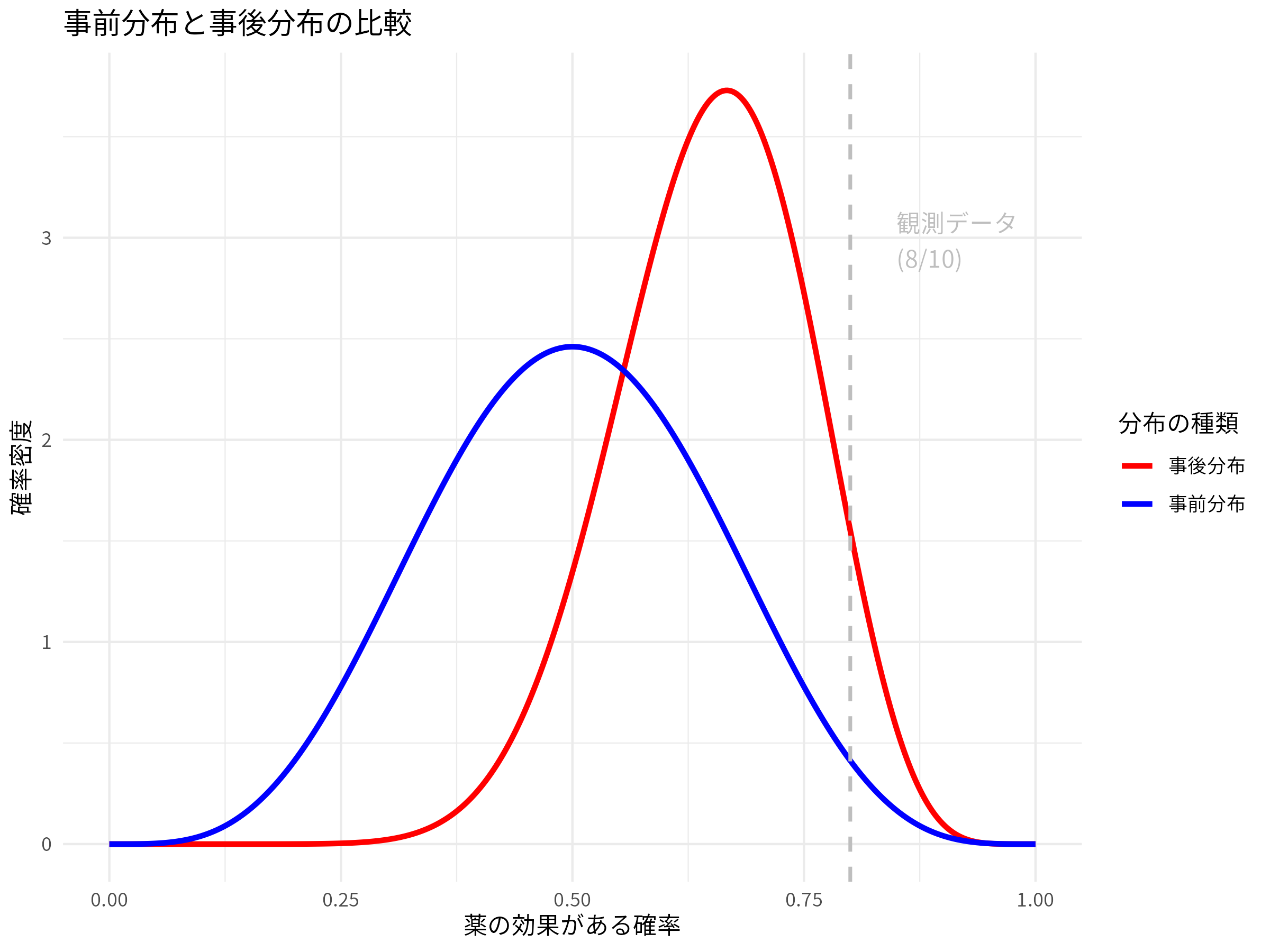
実行結果:
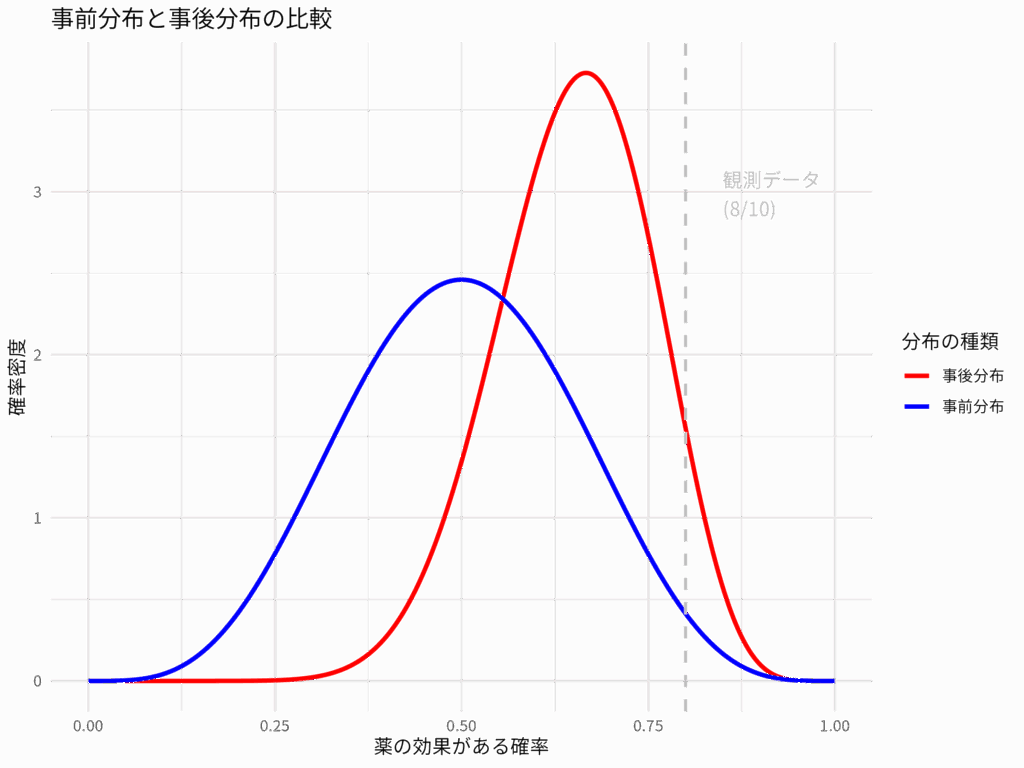
このグラフを見ると、青い線で示された事前分布は比較的幅広い範囲に広がっており、薬の効果に対するあなたの初期の不確実性を表している。しかし、赤い線で示された事後分布は、観測データ(10人中8人成功)の近くにピークが移動し、よりシャープになっていることがわかる。これは、データによって薬の効果に対するあなたの信念が更新され、より確信度が高まったことを示している。
まとめ
ベイズ統計学における事前分布と事後分布は、「データを見る前の知識」と「データを見た後の知識」をそれぞれ表し、データによって知識が更新されていくプロセスを明確に示している。宝探しの比喩のように、漠然とした期待が具体的な情報によって確信に変わるように、ベイズ統計学は私たちの「信念」がデータによって洗練されていく過程を理解するための強力な枠組みを提供してくれる。
あなたも、日々の生活の中で「これまでの経験」と「新しい情報」がどのようにあなたの判断を形成しているか、ベイズ統計の視点から考えてみてはどうだろうか?





コメント