私たちが生きる世界は不確実性に満ちている。明日の天気、新しい治療法の効果、マーケティングキャンペーンの成功率など、未来の出来事を完全に予測することはできない。しかし、この不確実性を数学的に捉え、合理的な意思決定を支援する強力なフレームワークが存在する。それが「ベイズの理論」であり、そこから発展した「ベイズ統計」である。本記事では、ベイズの理論の核心からベイズ統計へのつながり、その応用例、そして簡単なRコードでの計算例までを分かりやすく解説する。
ベイズ理論
ベイズ理論の根幹をなすのは、18世紀の牧師であり数学者であったトーマス・ベイズによって定式化されたベイズの定理である。ベイズの定理は、新しい情報（データ）が与えられたときに、ある仮説（または事象）の確率（信念）をどのように更新すべきかを示すものだ。
$$ P(H∣E)=\frac{P(E∣H)P(H)}{P(E)} $$
この式を構成する各要素は以下の通りだ。
- P(H∣E): 事後確率（Posterior Probability）。事象 E が起きた後での仮説 H の確率。私たちが知りたい「更新された信念」である。
- P(E∣H): 尤度（Likelihood）。仮説 H が真であるという条件下で、事象 E が観察される確率。
- P(H): 事前確率（Prior Probability）。事象 E が観察される前の仮説 H の確率。これは私たちの初期の信念や既存の知識を表す。
- P(E): 周辺尤度（Marginal Likelihood）。事象 E が観察される確率。これは通常、すべての可能な仮説について尤度と事前確率を合計（または積分）することで計算される。
簡単に言えば、ベイズの定理は「データを見る前に抱いていた信念（事前確率）を、新しいデータ（尤度）に基づいて更新し、より確からしい信念（事後確率）を得る」ためのルールなのだ。
ベイズ統計
ベイズ統計は、このベイズの定理を統計的推論に応用したものだ。従来の頻度論統計が、データが無限に繰り返される中で「真の値」が存在すると仮定し、その値が「有意」であるかどうかを判断するのに対し、ベイズ統計は未知のパラメーター（例えば、あるグループの平均や比率など）自体を確率変数として捉える。
ベイズ統計では、以下のステップで推論を進める。
- 事前分布の設定: 分析者がデータを見る前に持っている、未知のパラメーターに関する知識や信念を確率分布として表現する。これが事前分布（Prior Distribution）だ。
- 尤度の定義: データを生成する確率モデル（例えば、正規分布や二項分布など）を仮定し、未知のパラメーターの特定の値のもとでそのデータが観察される確率（尤度関数）を定義する。
- 事後分布の計算: ベイズの定理を用いて、事前分布と尤度関数を結合し、新しいデータが与えられた後の未知のパラメーターに関する信念を更新する。これが事後分布（Posterior Distribution）である。
得られた事後分布は、未知のパラメーターに関する私たちの最新かつ最も包括的な情報源となる。この分布から、パラメーターの最も確からしい値（事後平均や事後中央値）、信頼区間に相当する信用区間（Credible Interval）などを導き出し、意思決定に役立てる。
理論から統計へのつながり
ベイズ理論が「信念を更新するための一般的な数学的フレームワーク」であるのに対し、ベイズ統計は「そのフレームワークを統計的推論、つまりデータから未知の事柄を推測するプロセスに応用したもの」と言える。
具体的には、ベイズの定理のHを「未知のパラメーターの値」とみなし、Eを「観測されたデータ」とみなすことで、ベイズ統計が構築される。
- P(H): 未知のパラメーターに関する事前分布
- P(E∣H): パラメーターの値が与えられたときにデータが観察される尤度関数
- P(H∣E): データが観察された後の未知のパラメーターに関する事後分布
このように、ベイズの定理という理論的な柱を基盤として、データから学習し、不確実性を定量化し、信念を更新するという統計的な実践が可能になるのだ。頻度論統計が「仮説検定」を通じて結論を出すのに対し、ベイズ統計は「確率分布として不確実性を表現し、意思決定の材料とする」という点で異なる。
ベイズ統計の使い所
ベイズ統計は、特に以下のような場面でその真価を発揮する。
- データが少ない場合: 頻度論統計では十分なデータがないと安定した結果が得られにくいが、ベイズ統計は事前情報を活用することで、少ないデータからでも合理的な推論が可能だ。
- 事前情報が存在する場合: 過去の研究結果、専門家の意見、常識など、何らかの事前知識がある場合に、それを分析に組み込むことができる。
- 不確実性を明示的に扱いたい場合: 推定値の点推定だけでなく、その値が取りうる範囲（信用区間）や確率分布全体を知りたい場合に有効だ。
- 意思決定支援: 推定結果を確率的な言葉で表現できるため、リスクを考慮した意思決定に役立つ。
- 複雑な階層構造を持つデータ: 医療データや教育データなど、個体、グループ、地域といった階層構造を持つデータに対して、階層ベイズモデルが強力なツールとなる。
具体例と簡単な R 計算例
ある新薬が特定の疾患に効果があるかを確認する臨床試験を考えてみよう。この疾患の標準治療に対する新薬の有効性を評価したいとする。
シナリオ:
- 過去の経験から、この疾患の標準治療では約20%の患者に効果があると知られている。
- 新薬を10人の患者に投与したところ、4人に効果が見られた。
このデータから、新薬の有効性（効果がある確率 p）が標準治療よりも高いと言えるだろうか？
ベイズ統計では、この効果がある確率 p を確率変数として扱う。
- 事前分布の設定:新薬の効果 p について、データを見る前の私たちの信念を表す分布を設定する。今回は、過去の経験から「標準治療では20%」という情報があるため、pが0.2付近にある可能性が高いという事前情報を取り入れたいとする。ベータ分布は確率の事前分布としてよく用いられる。ここでは、平均が0.2となるようなベータ分布 $\text{Beta}(\alpha, \beta) $ を仮定しよう。例えば、$\alpha=2, \beta=8$ とすると平均は $\frac{\alpha}{\alpha+\beta} = \frac{2}{2+8}=0.2$ となる。
- 尤度関数の定義:10人中4人が効果を示したというデータは、二項分布に従うと考えられる。$P(\text{data}∣p)=\text{Binomial}(10,4,p)$
- 事後分布の計算:ベータ分布と二項分布の組み合わせは、事後分布もベータ分布になるという便利な性質（共役事前分布）がある。事後分布のパラメーターは、$\alpha_\text{posterior}=\alpha_\text{prior}+\text{成功数}、\beta_\text{posterior}=\beta_\text{prior}+\text{失敗数} $となる。今回のケースでは、成功数=4、失敗数=10-4=6 なので、$\alpha_\text{posterior}=2+4=6, \beta_\text{posterior}=8+6=14$したがって、事後分布は $\text{Beta}(6,14)$ となり、その平均は、$6/(6+14) = 6/20 = 3/10 = 0.3$ となる。
簡単なR計算例
Rを使って、これらの分布を視覚化し、事後分布から推定値を得てみよう。
R スクリプト例：
# 事前分布のパラメータ
alpha_prior <- 2
beta_prior <- 8
# 観測データ
successes <- 4 # 効果があった患者数
trials <- 10 # 投与した患者数
failures <- trials - successes # 効果がなかった患者数
# 事後分布のパラメータ
alpha_posterior <- alpha_prior + successes
beta_posterior <- beta_prior + failures
# pの取りうる範囲
p_values <- seq(0, 1, length.out = 1000)
# 事前分布の確率密度
prior_density <- dbeta(p_values, alpha_prior, beta_prior)
# 事後分布の確率密度
posterior_density <- dbeta(p_values, alpha_posterior, beta_posterior)
# プロット
par(mar = c(5, 5, 4, 2), cex.main = 1.5, cex.lab = 1.5, cex.axis = 1.5)
plot(p_values, prior_density,
type = "l", col = "blue", lwd = 2,
main = "事前分布と事後分布の比較",
xlab = "新薬の効果がある確率 (p)", ylab = "確率密度",
ylim = c(0, max(prior_density, posterior_density) * 1.1)
)
lines(p_values, posterior_density, col = "red", lwd = 2)
legend("topright", legend = c("Prior", "Posterior"), col = c("blue", "red"), lwd = 2, cex = 1.5)
# 事後分布の平均と95%信用区間
posterior_mean <- alpha_posterior / (alpha_posterior + beta_posterior)
credible_interval <- qbeta(c(0.025, 0.975), alpha_posterior, beta_posterior)
print(paste("事後分布の平均:", round(posterior_mean, 3)))
print(paste("95%信用区間:", round(credible_interval[1], 3), "-", round(credible_interval[2], 3)))
実行結果：
> print(paste("事後分布の平均:", round(posterior_mean, 3)))
[1] "事後分布の平均: 0.3"
> print(paste("95%信用区間:", round(credible_interval[1], 3), "-", round(credible_interval[2], 3)))
[1] "95%信用区間: 0.126 - 0.512"結果解釈
上記のRコードを実行すると、次のような結果が得られる。
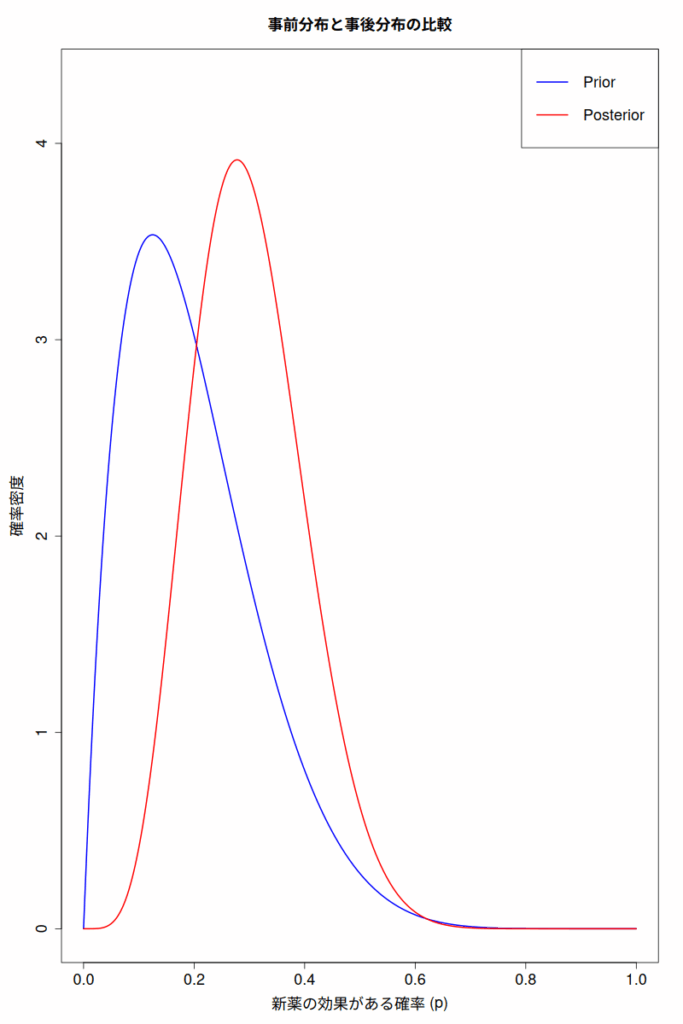
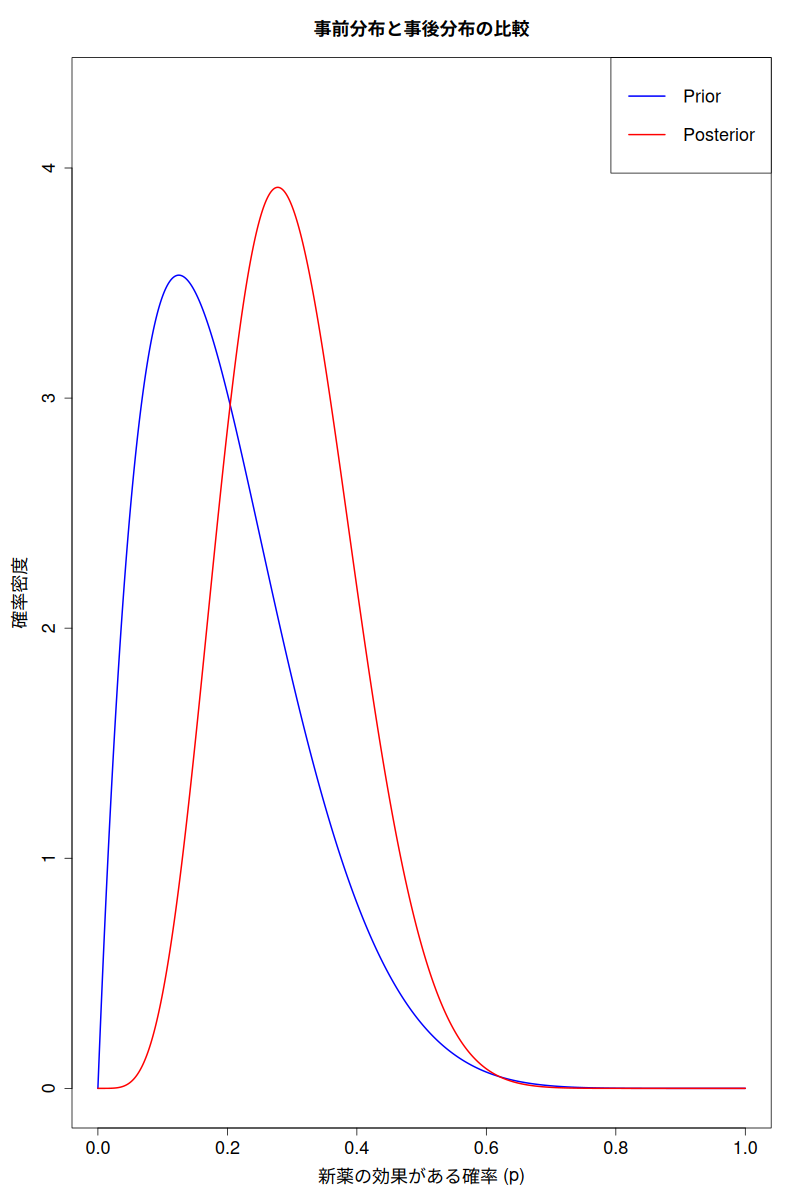
- 事前分布（青線）は、新薬の効果が20%あたりに中心があることを示している。これは、データを見る前の私たちの初期の信念だ。
- 事後分布（赤線）は、データ（10人中4人に効果）を考慮した後の新薬の効果の確率分布である。この分布は事前分布よりも右にシフトし、より狭くなっているはずだ。これは、新しいデータによって「効果がある確率 p」に関する私たちの信念が更新され、不確実性が減少したことを意味する。
- 事後分布の平均は、新薬の効果の最も確からしい値を示す。上記の例では、0.3（30%）になるだろう。
- 95%信用区間は、新薬の効果の真の値が95%の確率でこの範囲内にあると私たちが信じる区間である。例えば、[0.126, 0.512] のような結果が得られれば、「新薬の効果がある確率は95%の確率で12.6%から51.2%の間にある」と解釈できる。
この結果から、「新薬の効果が標準治療の20%よりも高い可能性」について、確率的な評価を行うことができる。事後分布が20%よりも高い値にどれくらいの確率を割り当てているかを直接確認できるのが、ベイズ統計の強力な点である。
まとめ
ベイズの理論は、新しい情報に基づいて信念を合理的に更新するための数学的な指針を提供する。そして、ベイズ統計は、この理論をデータから未知の事柄を推論するという統計的な問題に応用したものだ。事前情報を活用し、不確実性を確率分布として明示的に表現できるベイズ統計は、データが少ない状況や複雑な問題を扱う際に特に強力なツールとなる。
従来の統計学とは異なるアプローチを提供することで、ベイズ統計は私たちのデータ分析と意思決定の方法に新たな視点をもたらしている。不確実な世界でより良い意思決定を行うために、ベイズ統計は今後ますます重要な役割を担っていくことだろう。
コメント