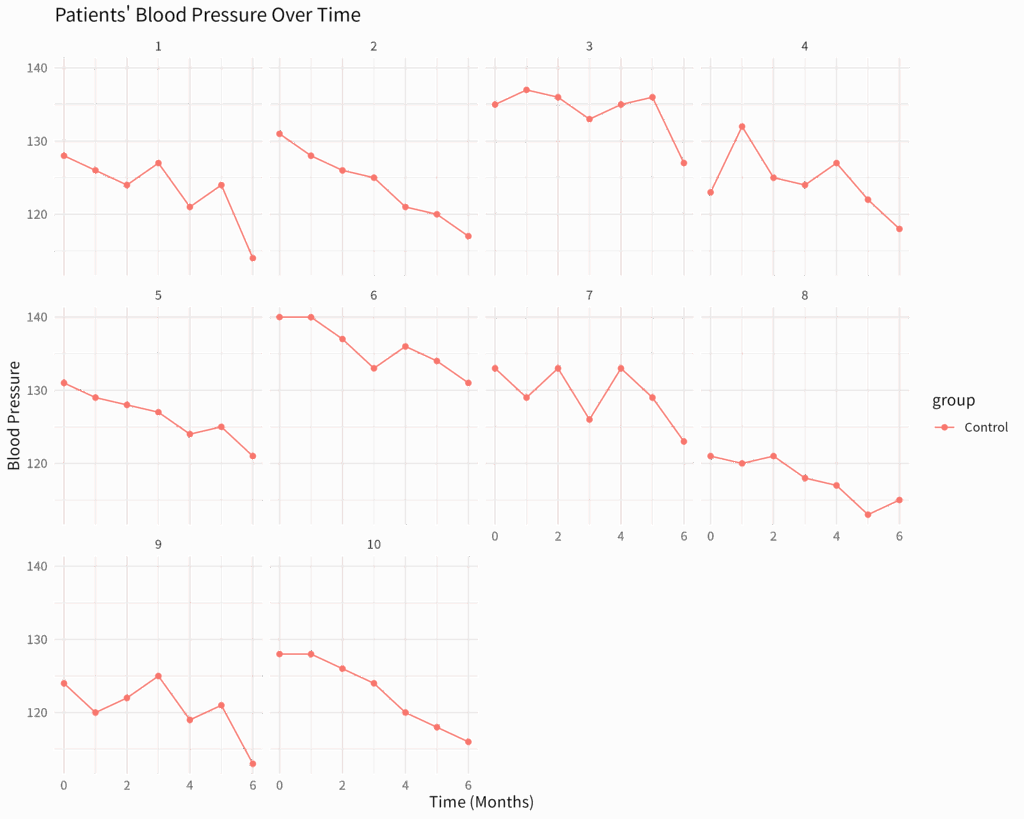-

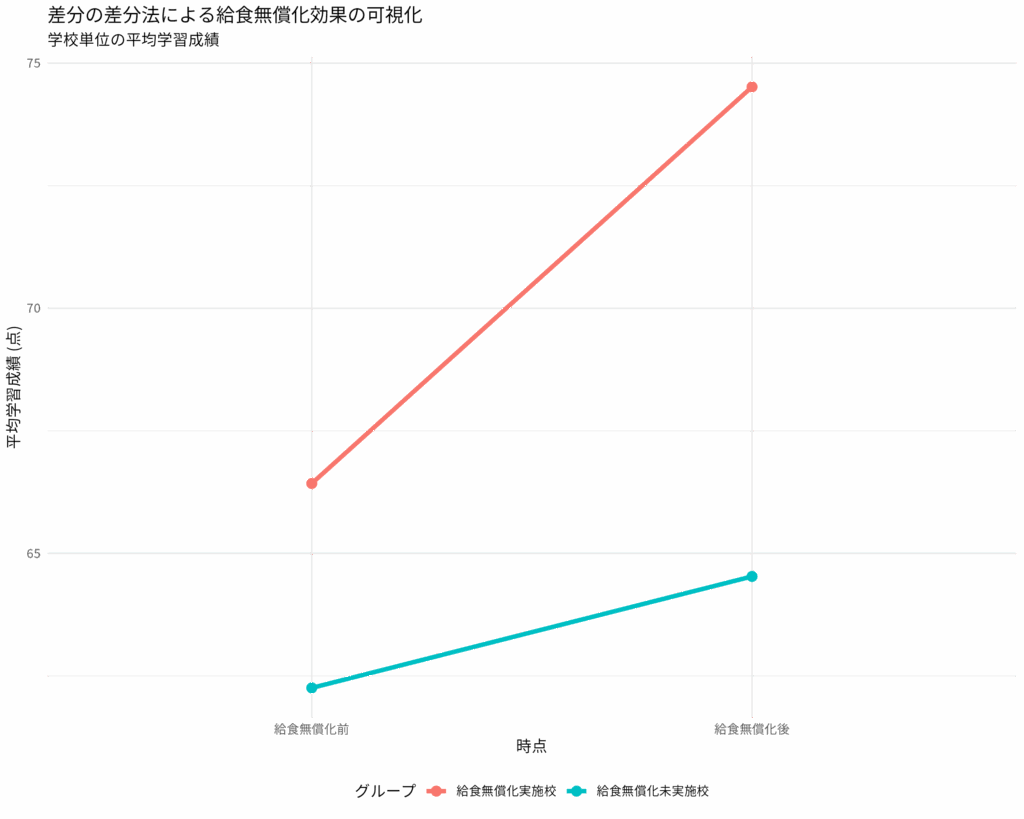
差分の差分法を理解する:因果推論の強力なツール
差分の差分法(Difference-in-Differences, DiD)は、政策変更や介入の効果を評価する際に非常に強力な統計的手法だ。この記事では、DiDの基本的な考え方から、その使い所、関連する統計手法との違い、DiDの核心である並行トレンドの仮定について詳しく解... -

操作変数法を徹底解説!見せかけの相関にだまされないための強力な武器
見せかけの相関に惑わされていないだろうか?世の中には、一見すると関係がありそうに見えて、実はそうではない現象がたくさん存在する。例えば、「アイスクリームが売れるとプールの事故が増える」という話を聞いたことはないだろうか?これは、アイスク... -

SEMにおけるMIMICモデル:潜在変数で測定誤差を考慮した分析を
SEM(構造方程式モデリング)は、心理学や社会学といった分野で複雑な因果関係を分析する際に非常に強力なツールとなる。しかし、アンケート調査などで収集されるデータには、回答者の個人的な解釈の違いや測定尺度の不完全性から生じる「測定誤差」がつき... -

媒介効果と調整効果:2つの「影響」を理解する
研究論文やデータ分析でよく耳にする「媒介効果」と「調整効果」。どちらも変数間の関係性を深く掘り下げる際に重要な概念であるが、その意味するところは大きく異なる。本記事では、これら二つの効果の違いを明確にし、具体的な例とRでの計算例を交えなが... -

媒介因子、媒介変数、媒介分析を徹底解説! データ分析の奥深さを知る
データ分析を進める上で、「ある原因が結果にどう影響するか」を直接的に見るだけでなく、その間に存在する「別の要因」の存在を意識することは非常に重要だ。この「別の要因」が、ときに原因と結果の関係性をより深く理解するための鍵となる。今回は、こ... -

媒介因子とは?研究デザインにおける重要な概念を徹底解説
疫学研究や社会科学研究において、ある事象が別の事象に影響を与えるメカニズムを解明することは非常に重要である。しかし、単に「AがBを引き起こす」というだけでなく、その間に別の要因が介在することがよくある。このような時に登場するのが「媒介因子... -

Rで実践!構造方程式モデリング:複雑な関係性を解き明かす強力なツール
構造方程式モデリング(SEM)は、社会科学、心理学、マーケティングなど、多岐にわたる分野で活用されている統計分析手法である。観測されたデータから、直接観測できない潜在的な変数間の因果関係や複雑なパスを統計的に推定・検定することが可能である。... -

欠測値の対処法:研究と分析を成功させるためのロードマップ
研究やデータ分析において、欠測値 (Missing Values) は避けて通れない問題である。データの一部が欠けていると、分析結果の信頼性が損なわれたり、偏った結論が導き出されたりする可能性がある。しかし、適切な対処法を知っていれば、この課題を克服し、... -

Full Information Maximum Likelihood (FIML) による欠損データ処理:概要とRでの実践
データ分析を行う際、欠損データは避けて通れない課題の一つである。単純な欠損処理方法では情報が失われたり、結果に偏りが生じたりする可能性がある。そこで注目されるのが、Full Information Maximum Likelihood(FIML)である。FIMLは、欠損データを統... -

欠測率の計算方法と論文への記載方法:研究の信頼性を高めるために
研究データには、しばしば「欠測値(Missing Values)」という問題がつきまとう。この欠測値を適切に処理することは、研究結果の信頼性や妥当性を確保するために不可欠である。本記事では、欠測率の基本的な計算方法から、統計解析ソフトウェアRを用いた具... -

多重代入法後のCox回帰:Wald検定(ANOVA)カイ二乗値の統合
多重代入法 (Multiple Imputation, Mice) は、欠損値に対処するための強力な統計的手法である。しかし、多重代入法によって作成された複数のデータセットそれぞれに対して統計解析を行った後、それらの結果をどのように統合すればよいか迷うことがある。本... -

クラスターランダム化比較試験の基礎:研究デザインと適切なサンプルサイズ計算
従来のランダム化比較試験(RCT)は、個々の参加者をランダムにグループに割り付けることで、介入の効果を公平に評価するための強力な手法である。しかし、医療や教育の現場では、個人ではなくグループ(クラスター)単位で介入が行われることが少なくない... -

尺度開発 信頼性・妥当性研究論文リスト
随時追加していく 看護学分野 退院後早期の育児不安尺度の開発と信頼性・妥当性の検討 産後2週間の母親373名を対象とした調査で、育児不安尺度(20項目4因子:負担感、抑うつ気分、母乳不足感、児の哺乳の不安定感)の信頼性・妥当性が確認された。本尺度... -

線形混合効果モデル:反復測定データ解析の強力なツール
臨床研究や生物学研究において、同じ被験者から複数回測定されたデータ(反復測定データ)は頻繁に登場する。このようなデータは、従来の線形回帰モデルでは適切に解析できない場合がある。なぜなら、同じ被験者からの測定値は互いに相関を持つため、独立... -

信頼区間の重なりで「差」を判断してはいけない理由
2つのグループの平均値を比較する際、多くの人がそれぞれの平均値の95%信頼区間が重なっているかどうかを見て、「統計学的に有意な差があるか」を判断しようとする。しかし、これは誤りである。実は、2つの信頼区間が重なっていたとしても、統計学的に有意... -

生物学的同等性試験における90%信頼区間の重要性
新薬開発や後発医薬品(ジェネリック医薬品)の開発において、薬剤の有効性と安全性を科学的に評価することは極めて重要である。その中でも、すでに承認されている医薬品(先発医薬品)と新しい医薬品が、体内で同等に作用するかを評価する生物学的同等性... -

反復測定データの解析:EM平均を用いた群間・時点間比較
臨床研究では、同一の対象者に対して複数回測定を行う反復測定デザインが頻繁に用いられる。このようなデータは、時間経過に伴う変化や介入効果を評価する上で非常に有用だが、一方で、複雑な相関構造をモデル化するという課題がある。この複雑な相関構造... -

固定効果と変量効果:データ解析における「平均」と「個人差」の捉え方
医療研究や社会調査など、さまざまな分野のデータ解析で登場する固定効果と変量効果。これらは、データを回帰モデルで分析する際に、「集団全体の平均的な傾向」と「個々の対象が持つ固有のばらつき」をどのように扱うか、という考え方に基づいている。 固... -

一般化推定方程式(GEE)の基礎と臨床研究での応用
臨床研究や疫学研究において、繰り返し測定されるデータやクラスター化されたデータは頻繁に登場する。このようなデータでは、同じ被験者からの測定値や同じクラスター内の観測値には相関があるため、従来の独立性を仮定する統計手法では適切な解析ができ... -

一般化線形混合モデル(GLMM)の基本と応用
臨床研究や生物統計学の分野では、患者ごとのばらつきや測定の反復性など、データが持つ複雑な構造を考慮することが不可欠である。しかし、基礎的な統計モデルでは、このような複雑性を十分に捉えきれない。そこで必要となってくるのが、「一般化線形混合... -

同等性検定と必要サンプル数計算:臨床研究における実践的アプローチ
新しい治療法が既存のものと同等であることを証明したい。そんな時、従来の「優れているか」を問う研究だけでは不十分である。本記事では、臨床現場で役立つ同等性検定の基本から、医師が直面する具体的なケースでの活用法、そして研究の成功に不可欠な必... -

統計的推測のその先へ:効果量の計算と実践
研究論文や統計解析の結果を目にしたとき、「有意差があった」という報告に接する機会は多い。しかし、P値が示す統計的有意性は、あくまで偶然によるものか否かという確率的な指標に過ぎない。では、その研究によって「どれくらいの効果があったのか」「そ... -

効果量とサンプルサイズの関係性:統計的検出力の向上を目指して
統計的仮説検定は、日々直面する様々な疑問に科学的に答えを出すための強力なツールである。特に医療や教育といった分野では、新しい治療法や学習方法の効果を検証する際に不可欠である。この検証の鍵を握るのが「効果量」と「サンプルサイズ」。これら二... -

有意水準、検出力、サンプルサイズ:統計的仮説検定の三位一体
統計的仮説検定は、科学研究やビジネスにおいて意思決定を行う上で不可欠なツールである。しかし、その結果を正しく解釈し、適切な結論を導き出すためには、「有意水準」「検出力」「サンプルサイズ」という三つの重要な概念の相互関係を理解することが不... -

R で感度・特異度分析に必要なサンプル数を計算する方法
診断検査の感度・特異度分析におけるサンプルサイズ計算は、研究の目的、疾患有病率、期待される感度・特異度、許容誤差、検出力に基づいて行われる。小さすぎると信頼性が低く、大きすぎるとリソースが無駄になる。統計的に信頼できる結果を得るには、こ... -

R で適合度の検定に必要なサンプル数を計算する方法
「あなたのデータ、本当にその仮説に合ってる?」📈 統計分析でよくあるこの疑問。 今回は、観測されたデータが、ある理論的な分布や比率にどれくらい「適合しているか」を科学的に評価する「適合度検定」について、基本から具体例、必要なサンプル... -

R でマクネマー検定に必要なサンプル数を計算する方法
「治療前後の効果」「施策による意識の変化」など、同じ対象者の2つの時点での変化を知りたいとき、マクネマー検定が役立つ。この検定は2値データ(はい/いいえなど)の変化を分析するのに最適。 この記事では、マクネマー検定の基本から、Rを使った計算例... -

傾向スコア法でバランスが取れないときの対処法
バランスが取れないときの対処法 共変量を見直す 傾向スコア作成のための共変量は、アウトカムに関連があり、要因にも関連があるものが候補である だが、要因にしか関連ないものは、除くとよい その観点で見直すと良い 参考:傾向スコア作成の際の変数の選... -

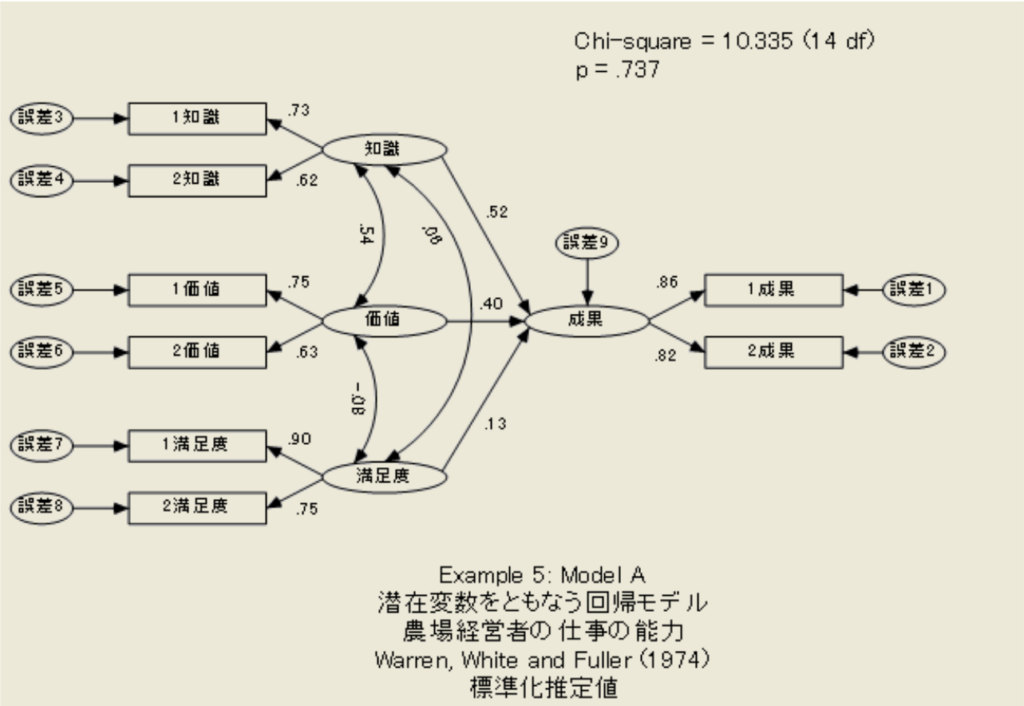
共分散構造分析の例と参考書籍
共分散構造分析は、構造方程式モデリング SEM とも呼ばれる、変数間の相関を元に、想定する概念モデルにデータが当てはまっているか、変数同士の関連性は強いのか弱いのか、ということを検討する手法である 具体的な事例が掲載されている論文および実践す... -

EZR と R を使って中央値に最小値・最大値のエラーバーがついた折れ線グラフを書く方法
反復測定データの各時点の中央値及び最小値・最大値を示したエラーバーがついた折れ線グラフを書きたいという要望はよく聞くが、そのようなグラフを書けるソフトウェアはなかなか見つからない EZR と R で中央値に最小値・最大値エラーバー付きの折れ線グ... -

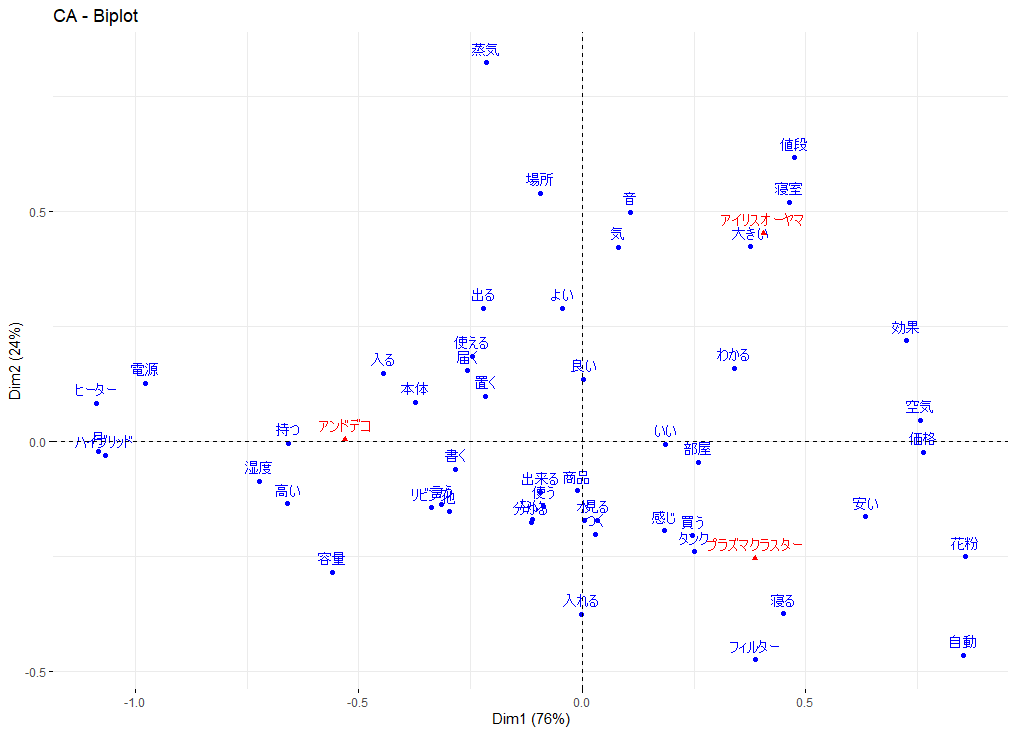
R でテキストマイニングを行い対応分析でバイプロットを書く方法
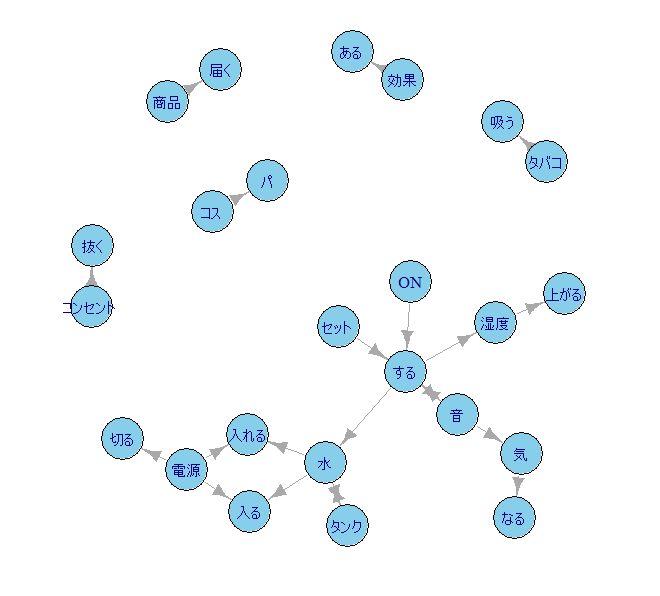
R で形態素解析を行い、外部変数との対応分析を実行し、バイプロット(biplot)を書く方法の解説 前準備:データの読み込みから外部変数で分割したファイルの保存 テキストデータは、例えば、以下のようなデータを準備する ここで、comment が分析対象のテ... -

R でテキストマイニングを行い頻度表を作成し n-gram を書く方法
R でテキストデータを単語に区切り、頻度表を作成して、N-gram を書く方法を解説 テキストデータの読み込みから頻度表作成まで まず、前提として、MeCab と RMeCab をインストールしておく MeCab と RMeCab の準備については、以下の関連記事を参照 まず、... -

EZR でサンプルの IPTW 背景データのサマリー表を出力する方法
EZR で IPTW を作成したのち、IPTW 背景データのサマリー表を作成したい場合どうしたらよいか IPTW 背景データのサマリー表作成手順全体像 EZR で IPTW(逆確率重み)を作成したのち、IPTW 背景データの集計表を作成したい場合、どのようにしたらよいか 具... -

R の解析結果をきれいにエクセルに貼り付ける方法
R の解析結果をきれいにエクセルに貼り付けられると、とても助かる 簡単きれいにエクセルに貼り付ける方法のご紹介 clipr パッケージを使用する方法 clipr パッケージを使うと簡単である 使用する前にインストールしておく install.packages("clipr") 例え... -

傾向スコア作成時に説明変数はいくつ入れてよいのか
傾向スコア作成時に、説明変数はいくついれてもよいのだろうか 最終モデルに交絡因子をたくさん入れないようにしたくて傾向スコアを使いたい場合利点があるのだろうか ロジスティック回帰分析における説明変数の数 傾向スコアは、ロジスティック回帰分析モ... -

傾向スコアを利用した解析
傾向スコアは、処方意向の確率を、背景因子で推測するという枠組みで計算される数値である 傾向スコアを用いることで、観察データを使用した、仮説に基づいた比較ができることになる 実際の利用方法を簡単に解説する 傾向スコアを利用した解析の総論 臨床... -

Mac に EZR をインストールすると英語版になってしまう件の対処法 2025年 6 月現在最新情報
日本語MacにEZRをインストールすると英語になってしまって困っている人へ 暫定結論 いったん R の完全アンインストール → 参考ブログ:https://dr-wolf.hatenablog.com/entry/2023/12/12/055302 R をインストール(R は最新版で問題なさそう) XQuartz 2.8... -

傾向スコアを共変量にした調整はなぜダメなのか
傾向スコアを用いた解析はいくつか知られているが、傾向スコアを共変量にした解析は推奨されていない その理由は何か 傾向スコアを共変量にした調整は推奨されていない 傾向スコアを用いた解析は、主に以下の 4 つである 傾向スコアマッチング 傾向スコア... -

傾向スコア法の利点と交絡因子の決め方
傾向スコア法は、交絡因子調整という点では、線形の多変量解析、例えば重回帰分析やロジスティック回帰分析と同様である しかし、線形回帰モデルとは異なる利点が存在する どんなときに傾向スコア法を用いるのが良いのか 傾向スコア法と多変量解析の比較 ... -

重回帰分析の結果の書き方 ― 論文にはどの数値を書いたらよいか
教科書的には何を計算するかは決まっているが、論文にどの数値を掲載するかは決まっていない。 そういうときは、実例をもとに、まねするのが良いが、最低限の目安を示す。 回帰分析の結果の書き方の基本 一番大事な要素は、点推定値と95%信頼区間である。... -

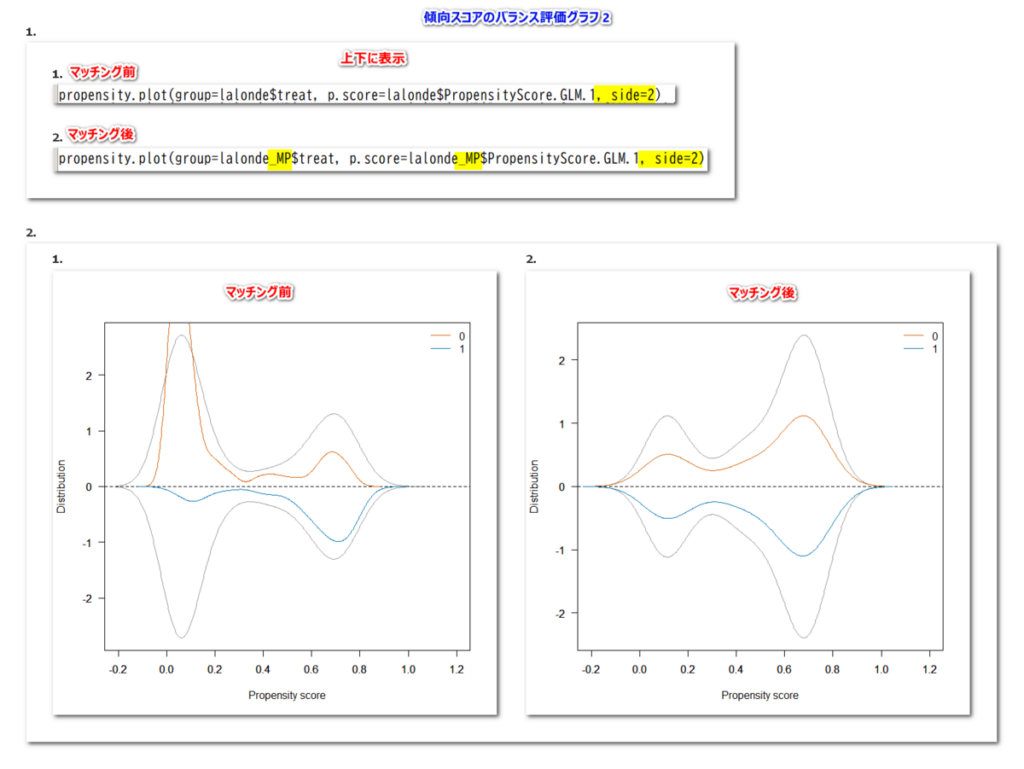
EZR で傾向スコアマッチングのバランス評価プロットを書く方法
傾向スコアマッチングの後に、バランス評価をするためのプロットを EZR で作成したいと考えた場合、どのようにするか 傾向スコアマッチングのバランス評価プロット 傾向スコアマッチングをした後に、マッチングのバランスを評価するプロットは、傾向スコア... -

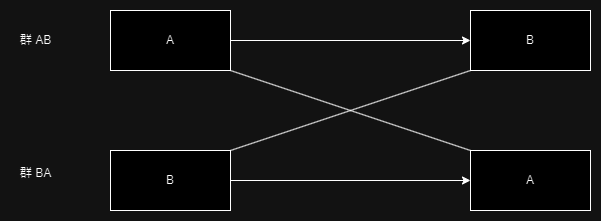
EZR でクロスオーバー試験データを解析する方法
クロスオーバー試験は、一人の症例が複数の介入を受けることで、並行群間試験よりも効率よく行える試験 EZR でクロスオーバー試験データを解析する方法を紹介する クロスオーバー試験とは クロスオーバー試験とは、介入 A と介入 B の両方を同じ被験者で行... -

EZR で IPTW カプランマイヤー 曲線の生存期間中央値と 95 % 信頼区間を計算する方法
EZR で IPTW(逆確率重み付け)カプランマイヤー曲線の生存期間中央値と 95 % 信頼区間を計算する方法を紹介する IPTW カプランマイヤー曲線とは何か? IPTW(逆確率重み付け) カプランマイヤー曲線とは、傾向スコアの逆数を用いた IPTW で交絡因子を調... -

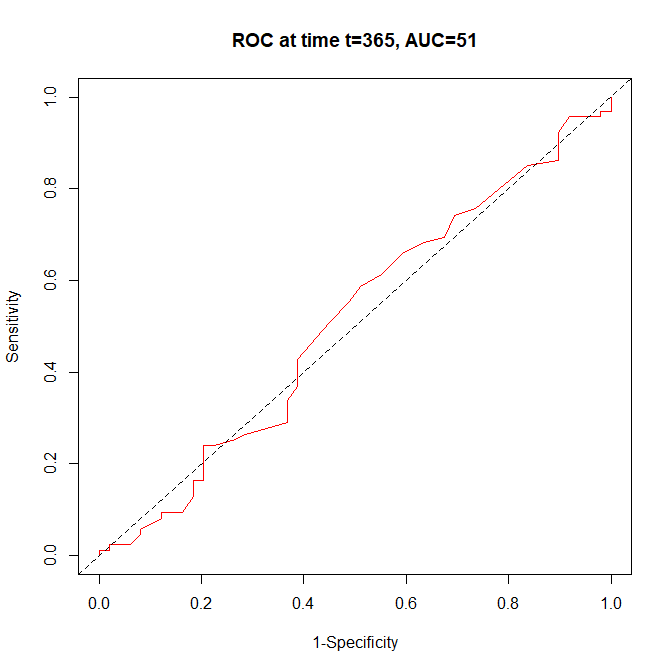
EZR で時間依存型 ROC 曲線 を比較する方法
EZR では、時間依存型 ROC 曲線の曲線下面積を求めることができる では、2 つの時間依存型 ROC 曲線の曲線下面積を比較することはできるだろうか? 時間依存型 ROC 曲線とは 時間依存型 ROC 曲線とは、生存時間イベントデータを予測する連続データのカット... -

SPSS と EZR で共分散分析の群間比較における主効果・単純主効果・EM 平均を求める方法
SPSS で、一般線型モデルなどで求めることができる EM 平均(調整平均、調整推定平均、推定周辺平均など呼び方はいろいろあり)は、EZR ではどのように求めればよいか、emmeans パッケージを使って計算してみた 因子が二つで交互作用を考える場合 計算メニ... -

EZR でスピアマンの順位相関係数の 95%信頼区間を計算する方法
EZR で Spearman の順位相関係数の 95%信頼区間を計算する方法 デフォルトでは計算できないが、パッケージをインストールすると計算できる EZR で Spearman の順位相関係数を計算する方法 統計解析 → ノンパラメトリック検定 → 相関係数の検定(Spearman ... -

EZR で効果量・事後検出力・事後サンプルサイズ計算を行う方法
統計解析を実施して、結果を見て初めて、検出力やサンプルサイズの問題が意識されることは多い 手元にすでにあるデータから効果量を計算し、事後検出力、事後サンプルサイズ計算に進む流れを紹介する 事後に検出力やサンプルサイズ計算が必要になることは... -

EZR で一人一行の反復測定データを一人複数行のデータに変換する方法
一人一行で反復測定データが入力されているときに、一人複数行のデータに変換したい場合、EZR ではどのようにするか? 反復測定データの準備方法には二つの方法がある 一人複数回測定しているデータの場合、一人一行で入力している場合(例:測定1、測定2... -

SPSS でフリードマン検定を行う方法
SPSS で対応のある多群のノンパラメトリック検定である、フリードマン検定を行う方法 概略 分析メニューのノンパラメトリック検定 → 対応サンプル というメニューから行う 対応サンプルのメニューを開いた後に、解析する変数を選択し、検定の種類を選択す... -

SPSS で複数条件を満たす症例ごとに分けたカテゴリカルデータを作成する方法
SPSS で複数の変数を組み合わせた条件で、新たなカテゴリカルデータを作成したいことがある 複数条件を満たす症例ごとに分けたカテゴリカルデータを作成する方法をご紹介 状況設定と方針 例として、以下の X1, X2 という 2 つの変数の組み合わせで、X3 と... -

SPSS でカテゴリ変数を別の区切りのカテゴリ変数にする方法
SPSS で、カテゴリ変数の区切り方を変えたい場合がある カテゴリ変数から別の区切りのカテゴリ変数を作成する方法 新しい区切りのカテゴリ変数の作成は「変換」から メニューバーの「変換」から、「他の変数への値の再割り当て」というメニューを選択する ... -

R で多重代入 IPTW Cox 回帰 ブートストラップ信頼区間を計算する方法
説明変数がいくつかある生存時間データで、いくつかの説明変数に欠損値があり、多重代入して IPTW Cox 回帰分析がしたい場合、R でどのようにすればよいか IPTW Cox 回帰の場合、ブートストラップ信頼区間がより適切であるが、それはどうやるか 多重代入と... -

R を使った多重代入で欠損値を補完した後、合計得点を計算して解析したい場合
多重代入法の際に、代入した変数を使って、合計得点などを計算して、最終的な解析がしたい場合がある そんなときに、どうすればよいか R で多重代入法を実施する方法の概要 R で多重代入法を行う基本的な方法は、以下の記事を参照 多重代入した後に変数同... -

R を使った多重代入法で欠損値を補完した後に Cox の Wald 検定のカイ二乗値を統合する方法
多重代入法で欠損値を補完した後に Cox 回帰の Wald 検定を統合する方法 多重代入法 多重代入法とは、欠損値を、取得されている変数から推測して、いくつかの値で補完して、いくつかのデータセットを作成し、解析したのち、結果を統合する方法 詳しくは、... -

EZR で多重代入法を行う方法
EZR で多重代入法を行いたい場合、どのようにしたらよいか EZR には、多重代入のメニューはないが、R スクリプト枠にスクリプトを書いていく方法で実行できる はじめに 欠損値(欠測値と同じ)があるデータセットにおいて、推定値にバイアスがかかると言わ... -

重回帰分析における当てはまりの良さに関するいくつかの指標の違いと使い分け
重回帰分析(以下、線形回帰も同義)には当てはまりの良さの指標としていくつかあるが、それらの違いと使い分けはどうしたらよいのか? 自由度調整済み決定係数の特徴 説明率とも言われる決定係数の説明変数の個数を考慮したバージョン 0 から 1 の間の値... -

決定係数が小さい場合の考え方
重回帰分析の評価指標の一つ、決定係数が小さいときに、どう考えたらよいか どのくらいの数値であったら、大丈夫なのだろうか 決定係数がどのくらいであれば意味があるか? 決定係数は、0.7 以上欲しいとか、0.5 でもよいとか、分野によっては 0.3 でもよ... -

標準化偏回帰係数の簡単な解説
標準化偏回帰係数(ひょうじゅんかへんかいきけいすう)とは何か? 一言で言えば、単位が異なる説明変数の、目的変数に対する影響力を比較したいときに、便利な数値と言える 順を追って、式なしでイメージだけでわかりやすく解説 標準化偏回帰係数の前に回... -

SPSS を使ってやりたい解析別重回帰分析の実行方法
SPSS で重回帰分析をしたい場合、どのようにすればよいか やりたいこと別にまとめてみた 説明変数が連続データの場合で、交絡因子調整が目的の場合 目的変数、説明変数ともに連続データで、交絡因子調整が目的の場合は、以下のように解析する 分析 → 回帰 ... -

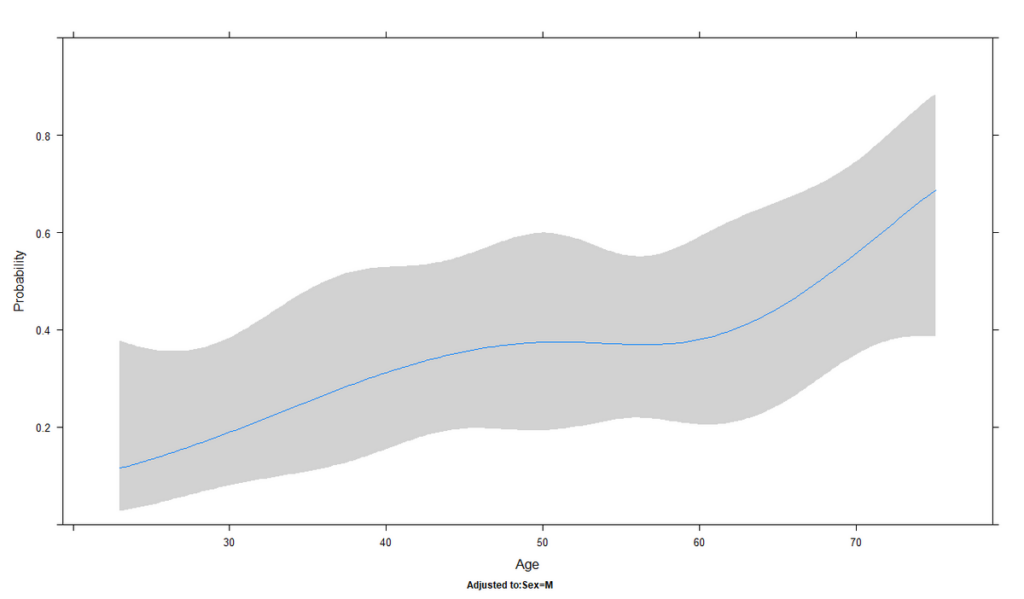
R で 制限付き 3 次スプライン曲線を二値アウトカムの場合に書く方法
制限付き 3 次スプライン曲線は、データの非線形関係をとらえるために書いてみるグラフのこと 二値のアウトカムの場合、R でどのように書くか紹介 制限付き 3 次スプライン曲線とは 制限付き 3 次スプライン曲線は、データの非線形関係をとらえるために用...