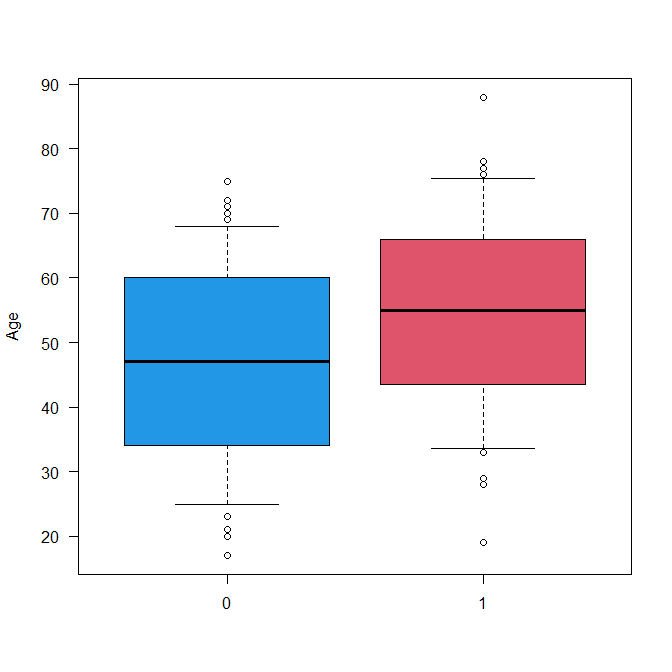-

統計解析における各種変数・データの呼び方を整理する
統計解析において、同じ意味合いで、違う呼び名が存在する それらを列挙して、整理したい 目的変数 研究の目的の項目、事項、事象、アウトカム、エンドポイントを測定、観測したデータのこと ほぼ同じ意味合いの言葉従属変数、応答変数、アウトカム、エン... -

R で IPTW の極端な重みを Trim によって Truncate する方法
IPTWにおける極端な重みのTruncation処理について 逆確率重み(IPTW)は、観察研究における交絡の調整手法として広く用いられているが、重みが極端な値をとる場合、推定量の分散が著しく増加し、結果が不安定になることがある そのため、極端な重みに対し... -

エクセルでデータ分析ボタンを表示させる方法
エクセルでデータ分析をしたいが、データ分析というボタンが見つからない エクセルで、データ分析がない場合の対処法 エクセルでデータ分析がない場合はファイルから まず、ファイルをクリック 次に、オプション(一番左下)をクリック アドイン → 分析ツ... -

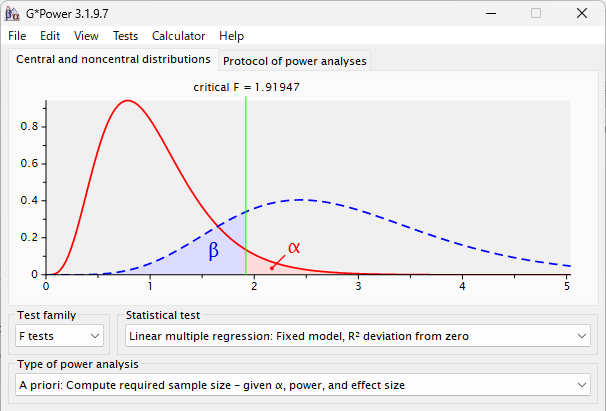
G*Power で重回帰分析に必要なサンプル数を計算する方法
G*Power は、サンプルサイズや検出力を計算するソフトウェアである 重回帰分析のサンプルサイズや検出力を計算する方法の紹介 GPower で重回帰分析のサンプル数を計算する方法 重回帰分析のサンプル数を計算するときは、予想される決定係数を見積もる必要... -

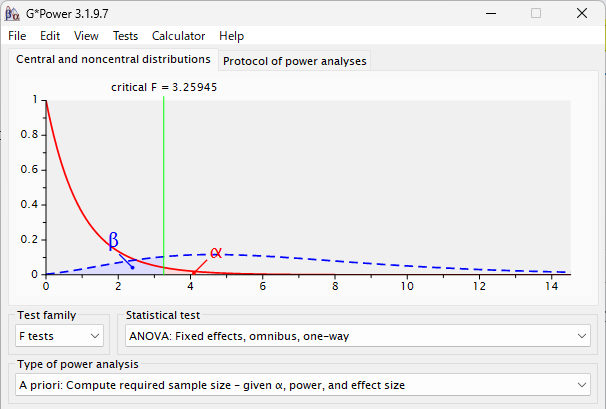
G*Power で分散分析に必要なサンプル数を計算する方法
G*Power は、サンプルサイズや検出力を計算するソフトウェア 分散分析の場合のサンプルサイズや検出力の計算方法の紹介 GPower で分散分析のサンプル数を計算する方法 3 群以上の群があるときに、いずれかの群が異なるかどうかを検討する場合に使う、一元... -

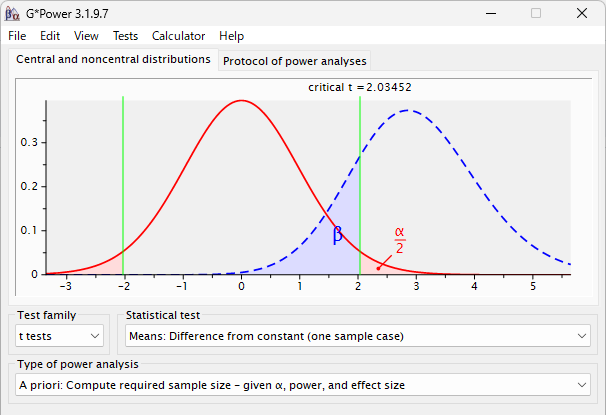
G*Power で対応のある t 検定に必要なサンプル数を計算する方法
GPower は、サンプル数を計算するソフトウェアである 事後検出力を計算することもできる 対応のある t 検定の場合の使い方を紹介 GPower で 対応のある t 検定のサンプル数を計算する方法 対応のある t 検定を使って、同じ人から 2 回測定して、その差を検... -

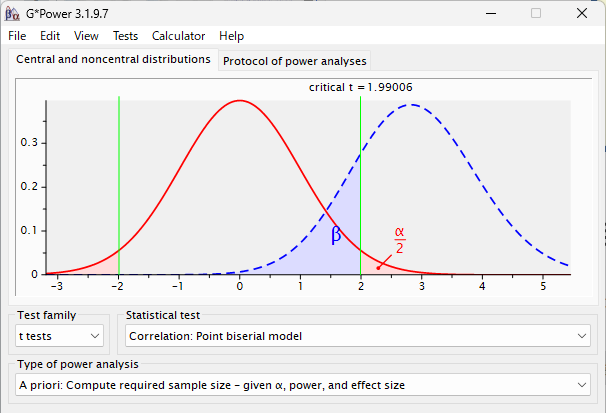
G*Power で相関係数に必要なサンプル数を計算する方法
G*Power は、サンプルサイズ計算ソフトである 相関を計算するのに必要なサンプル数を計算するときの使い方を解説する GPower で相関の必要サンプル数計算 G*Power での設定は以下のように行う Effect size に予想される相関係数を入れる 0.3 とすると以下... -

EZR で IPTW ロジスティック回帰を行う方法
IPTW ロジスティック回帰を EZR で行う方法 IPTW とは IPTW とは、日本語では逆確率重み付けと呼ばれる方法で、群間の交絡因子を調整する方法の一つ 詳しくは、こちらを参照のこと また、他の解析方法、例えば、IPTW Cox 回帰は、以下を参照のこと EZR で ... -

R で IPTW Cox 回帰を行う方法
IPTW 逆確率重み付け Cox 回帰を R で行う方法 IPTW Cox 回帰の前提 IPTW に関しては、こちらの記事を参照 IPTW はすでに作成済みというところから始める IPTW は、EZR で作成するのが簡単なので、EZR を使うことをお勧めする 以下の記事が参考になる IPTW... -

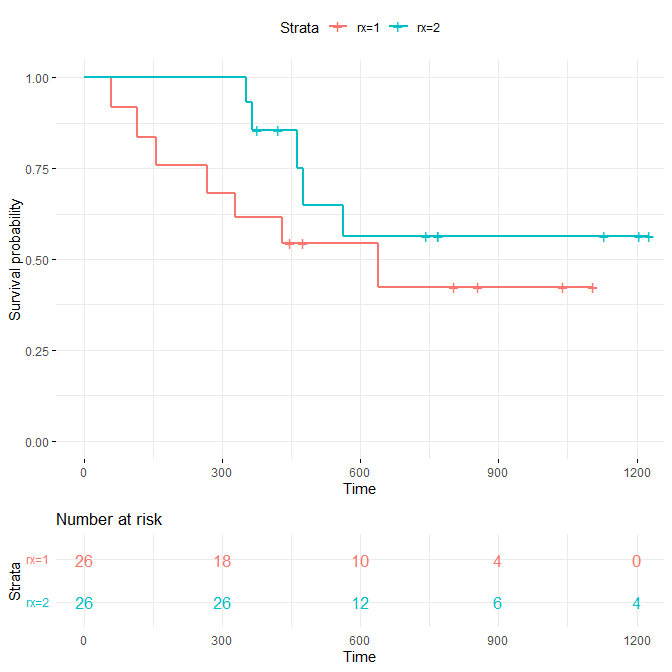
R で IPTW カプランマイヤー曲線グラフに Number at Risk を書き入れる方法
IPTW カプランマイヤー曲線において、任意の時点における Number at Risk を書き入れる方法 R で作成する方法 IPTW カプランマイヤー曲線 IPTW は、逆確率重み付けとも呼ばれ、ランダム割り付けしていない群間の交絡因子を調整する方法の一つ 詳しくはこち... -

論文におけるクラスカルウォリス検定の結果の書き方
クラスカルウォリス検定は、ノンパラメトリック版の一元配置分散分析 平均値というパラメータを使わないが、その結果はどのように書いたらよいか クラスカルウォリス検定はどんな計算をしているのか クラスカルウォリス検定は、連続データを順位に変換して... -

SPSS で線形混合モデルを実行する前にデータをワイドフォーマットからロングフォーマットへの変更する方法
SPSS で線形混合モデルを実行する場合、反復測定データを一人一行のワイドフォーマットからロングフォーマットへデータセットを変形する必要がある ワイドフォーマット(反復測定が横方向に並ぶ)からロングフォーマット(反復測定が縦方向に並ぶ)へ変更... -

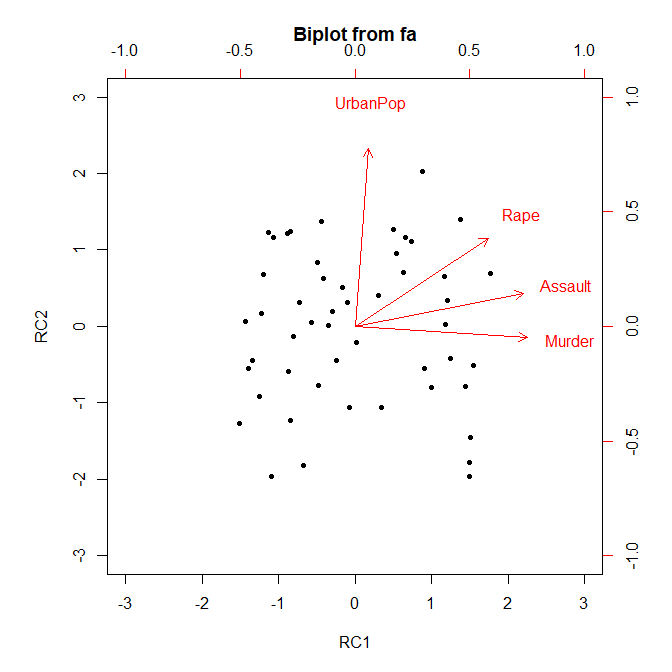
R と SPSS の主成分分析における主成分得点係数行列について
主成分分析 SPSS と R の比較をしてみる 主成分分析で主成分負荷量を計算する R は、psych パッケージの principal を使用する まず、psych パッケージをインストールする install.packages("psych") psych パッケージを呼び出して、principal を用いて主... -

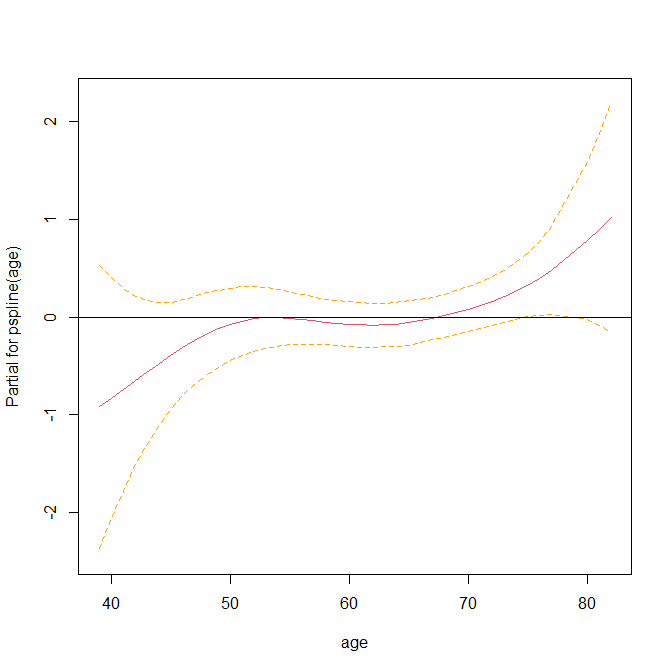
R で Cox 回帰を用いて Penalized Spline 曲線を書く方法
R で 生存時間データに対して、Penalized Spline(罰則付きスプライン)曲線を書く方法の解説 Penalized Spline とは Penalized Spline(罰則付きスプライン、P スプライン)は、データに合わせた滑らかな曲線を求めるために使われる方法の一つだが、過剰... -

論文におけるマンホイットニー U 検定の結果の書き方
ノンパラメトリック検定のマンホイットニー U 検定を実施した際に、p 値以外の結果はどのように書いたらよいのだろうか? マンホイットニーの U 検定 マンホイットニーの U 検定とは、母集団が正規分布しているかどうか、判断がつかない場合、母集団が正規... -

欠損値の分類 3 つとそれぞれの簡単な解説
欠損値(欠測値も同じ)は、生じる理由や前提から考えて、3 つに分けられるという話 欠損値とは 本来取得したかったデータで、取得できなかったデータのこと もともと取得できない・取得しなかったデータも同じ扱いなので、同じように欠損値と呼んでも問題... -

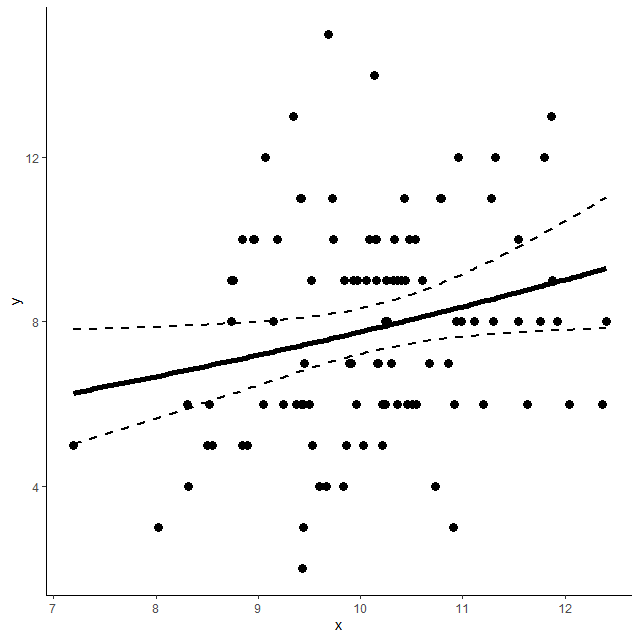
R でポアソン回帰の 95 % 信頼区間付き回帰直線のグラフを描く方法
カウントデータの散布図に、ポアソン回帰の回帰直線と予測値の 95 % 信頼区間を書き入れたグラフの書き方 ポアソン回帰 まれな事象が起きることを表現したポアソン分布を示すカウントデータ(発生数の数を数えたデータ)を予測する回帰モデル こちらも参... -

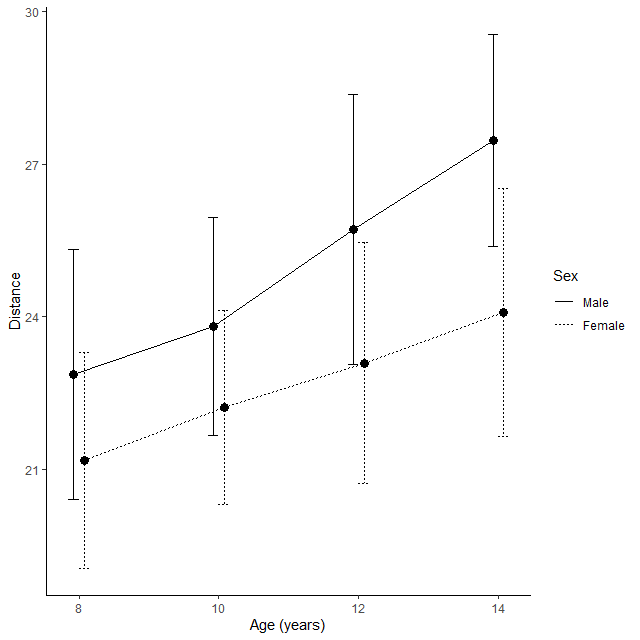
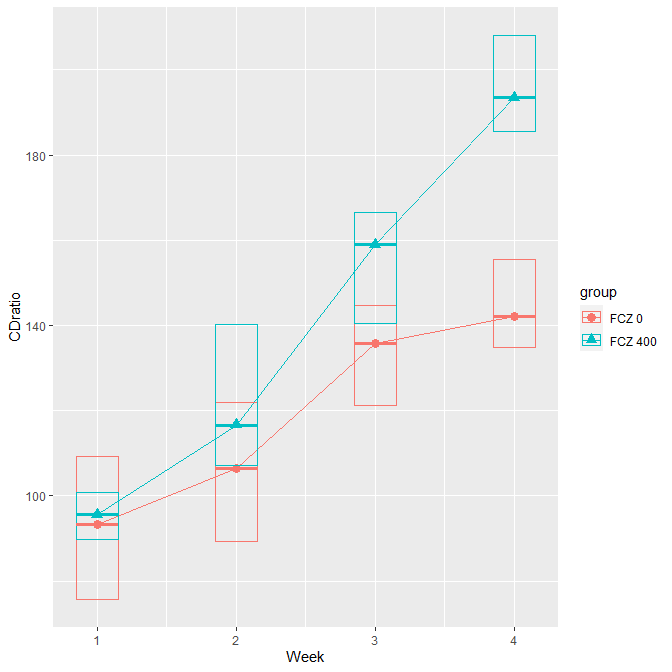
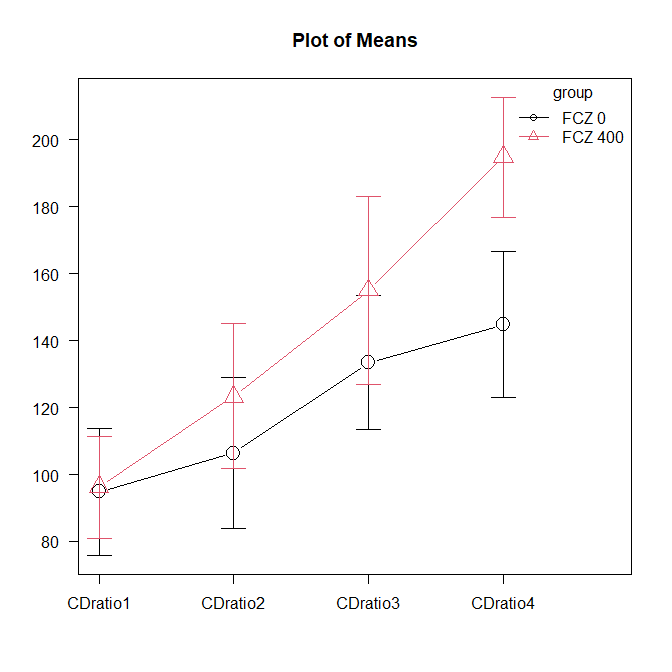
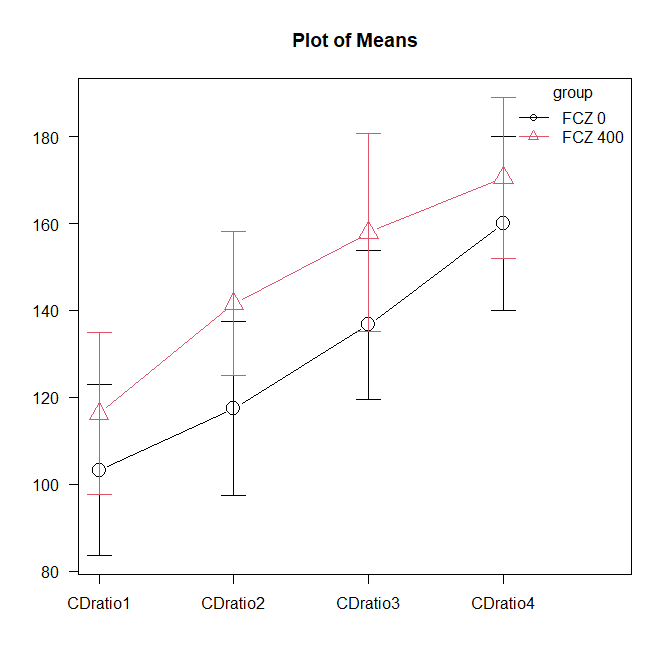
R で反復測定データの平均値の折れ線グラフを書く方法
反復測定データの群ごと時点ごとの平均値を結んだ折れ線グラフを書く方法 反復測定データと平均値の折れ線グラフ 反復測定データとは、同じ対象者がある決まった時点で何回か測定したアウトカムデータのことである 例えば、今回のサンプルデータのように、... -

EZR でポアソン回帰分析を行う方法
ポアソン回帰を EZR で行う方法の解説 ポアソン回帰・ポアソン分布とは ポアソン回帰とは、まれにしか起こらない現象を数えたカウントデータを目的変数にした回帰分析のこと カウントデータがポアソン分布に従うと仮定している 平均 $ \lambda $ 回起こる... -

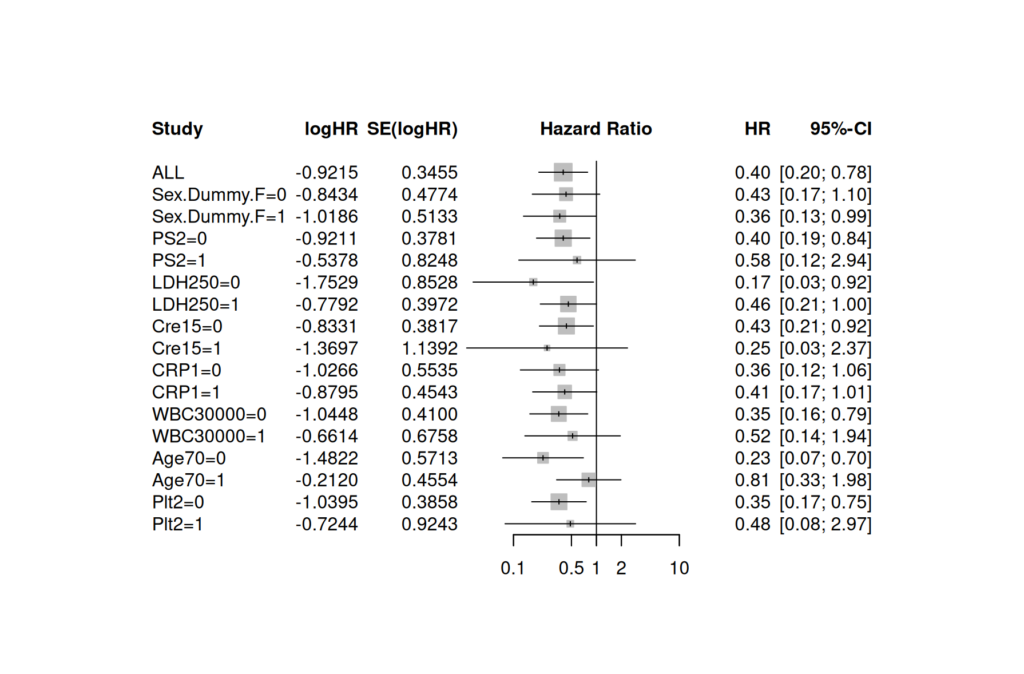
R でサブグループ解析の結果をフォレストプロットで書く方法
サブグループ解析の結果をフォレストプロットで書く方法はいくつかあるが、ここでは、R スクリプト中心に書く方法を解説する EZR の機能を使う方法 R のスクリプトの方法の前に、EZR のメニューをいろいろ駆使して書く方法の記事をご紹介 EZR になれている... -

R で IPTW 重回帰で行ってロバスト分散を用いた信頼区間を求める方法
IPTW 重回帰を実施した後、ロバスト分散から信頼区間を求める方法 ロバスト分散信頼区間を求める必要性 IPTW(逆確率重み付け)の元となる傾向スコアの値は、真の値ではなく、推定値であるため、通常の重み付き回帰のソフトウェアが出力する分散の推定量は... -

平均値の傾向検定をわかりやすく解説
グループごとの平均値が線形の傾向を示しているかどうかを検定する傾向検定をわかりやすく解説 平均値の線形傾向とは グループごとの平均値の線形傾向とは以下のような状態のことを言う 図の中の点は、平均値を表している 平均値を線で結んでいる図である ... -

分散分析に必要なサンプル数を計算したいと思った時に考えたほうがよいこと
分散分析のサンプルサイズ計算がしたいと思った時に考えるべきこと もしかしたら、あなたが必要なのは、分散分析のサンプルサイズ計算ではないかもしれない 分散分析のサンプルサイズ計算が必要と思った時には立ち止まる必要がある 分散分析をしなければな... -

SPSS でカイ二乗検定に必要なサンプル数を計算する方法
カイ二乗検定のサンプルサイズ計算を SPSS で行う方法 拡張機能のインストール 拡張機能 → 拡張ハブ を選択 検索窓に power と入力して、Power Analysis for Chi-Square Models を見つけて、拡張の取得にチェックを入れ、OK をクリック 規約に同意して、イ... -

R でカイ二乗検定に必要なサンプル数を計算する方法
カイ二乗検定のためのサンプルサイズ計算の方法 パッケージのインストール R の pwr パッケージをインストールして使用する install.packages('pwr') # 1 回だけインストール library(pwr) サンプルサイズ計算をする分割表の例 サンプルサイズ計算をする分... -

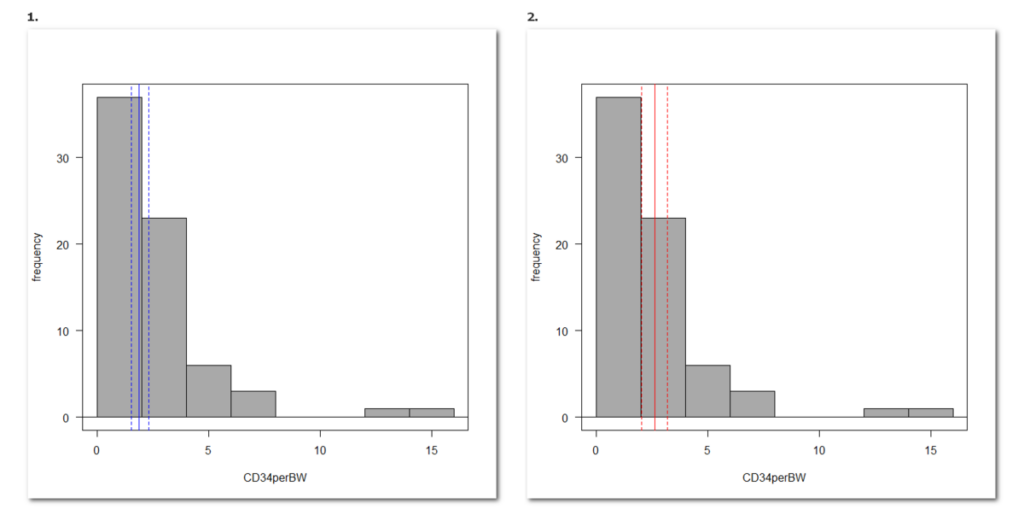
R で多重代入法を実行した後に Fine-Gray 回帰を行う方法
多重代入法で欠測値を補完し、Fine-Gray 回帰 を実施する方法 サンプルデータ 競合リスクを含むイベント変数、時間変数、着目したい変数、交絡因子を以下のとおりとする 競合リスクを含むイベント変数:CompRisk 時間変数:DaysFPS 着目したい変数:PS34 ... -

Mac で EZR を起動するためには RcmdrPlugin.EZR を適用する必要がある
Mac で EZR を使い始めるときに、EZR プラグインを当てて起動する方法 Mac で EZR を起動するために EZR プラグインの適用 EZR のインストールが終了したあと、ツール → Rcmdr プラグインのロード を選択 RcmdrPlugin.EZR が選ばれていることを確認して OK... -

因子分析の推定法の種類と使い分けについて簡単な解説
因子分析の推定法にはどんなものがあり、どう使い分けるか 因子分析の推定法 因子分析の推定法には、主に、最尤法、最小二乗法、重み付き最小二乗法の 3 つがある 因子分析の推定法 最尤法 最尤法は、精度よく推定できる サンプルサイズが十分大きいときに... -

ロジスティック回帰分析に投入する説明変数の数はいくつまでなら問題ないか
ロジスティック回帰の説明変数の数はいくつ入れてよいのか? ロジスティック回帰の説明変数の数 ロジスティック回帰分析をする場合、サンプルサイズによっていくつの説明変数を投入できるか サンプルサイズ諸論 の記述がもっともクリアでわかりやすい 二項... -

重回帰分析の説明変数に対数変換した変数がある場合の結果の書き方
説明変数を対数変換した場合の重回帰分析の結果の書き方 重回帰分析の結果の書き方 重回帰分析をはじめ、様々な回帰分析の結果の書き方を見比べられる、リンク集はこちら 重回帰分析の結果の書き方 対数変換した説明変数がある場合どう書くか 例 1 : ( lo... -

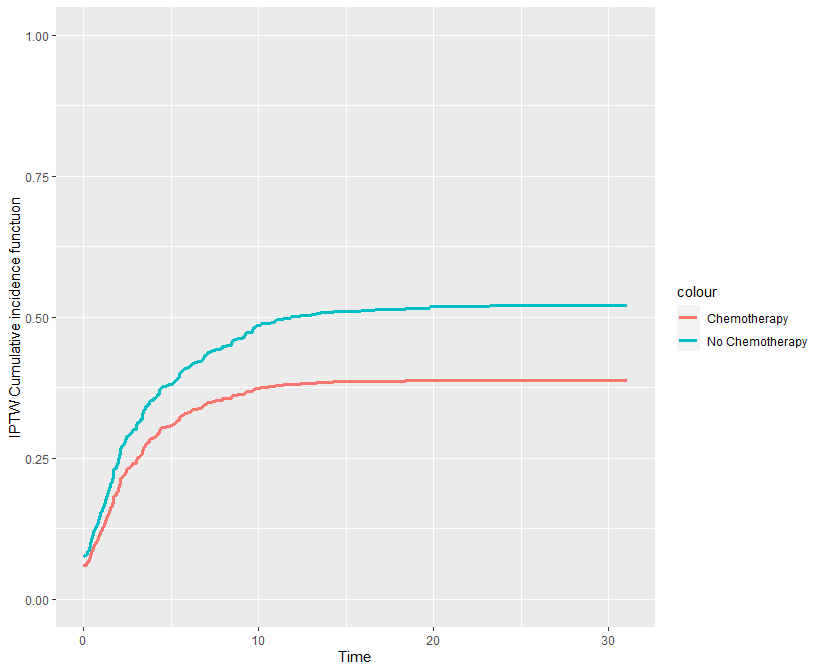
R で IPTW 競合リスク累積発生率曲線を書く方法
IPTW で重み付けした競合リスク累積発生曲線を書く方法 IPTW 競合リスク累積発生率曲線の書き方の前に IPTW、競合リスク、累積発生曲線とは? IPTW に関しては以下の過去記事を参照 競合リスクに関しては以下の過去記事を参照 累積発生率(累積イベント)... -

SPSS で二項検定を使って 3 群を多重比較する方法
SPSS で 3 群比較を二項検定を繰り返して行う方法 SPSS で 3 群比較する方法 多重比較 ここで言う、3 群比較&多重比較とは、3 群が同じ割合かどうかを、2 群ずつ確認する方法 3 群のうち、2 群のみを取り出し、二項検定を繰り返す 4 群以上も同様に行える... -

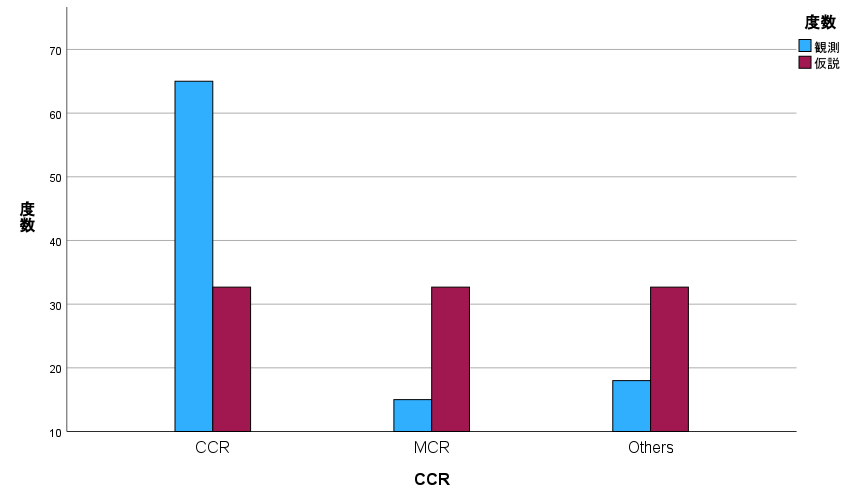
SPSS で適合度検定を使って 3 群を比較する方法
SPSS で 3 群が同じ割合かどうかを検定する方法 SPSS で 3 群比較する方法 検定の種類 ここで言う、3 群比較とは、3 群の割合が同じかどうかを検討することである すべての割合が同じと仮定した分布への適合度検定を行う ちなみに、4 群以上でも同様である... -

SPSS で二項検定を使って 2 群を比較する方法
SPSS で 2 群の比較をする方法の解説 SPSS で 2 群比較する方法 ここで言う 2 群比較というのは、2 群の割合の比較のことであり、半々かどうかの検定という意味である つまり、二項分布を使った二項検定のことである まず、分析 → ノンパラメトリック検定 ... -

R で中央値の折れ線グラフを描く方法
反復測定データを用いて、時点ごとの中央値を計算した後、折れ線グラフを書く方法 中央値の折れ線グラフの前に 平均値の折れ線グラフ 中央値の折れ線グラフの前に、平均値の折れ線グラフを示す ここでは、平均値の折れ線グラフとは、以下のようなグラフを... -

EZR で平均値の折れ線グラフを書く方法
EZR で反復測定データの時点ごとの平均値を結んだ折れ線グラフを書く方法の解説。 EZR で平均値の折れ線グラフを書くデータの準備 まず、下記のようなデータを用意する。 一人一行で、列方向に反復測定データを並べたデータである。 EZR で平均値の折れ線... -

SPSS で連続データをカテゴリ化する方法
SPSS で連続データを区切ってカテゴリカルデータを作る方法を解説 SPSS で連続データをカテゴリカルデータにする方法 例 1 :変数の計算 年齢を 10 歳の区切りでカテゴリカルデータにしたい場合 10 で割って小数点以下を切り捨てるという方法を使う まず、... -

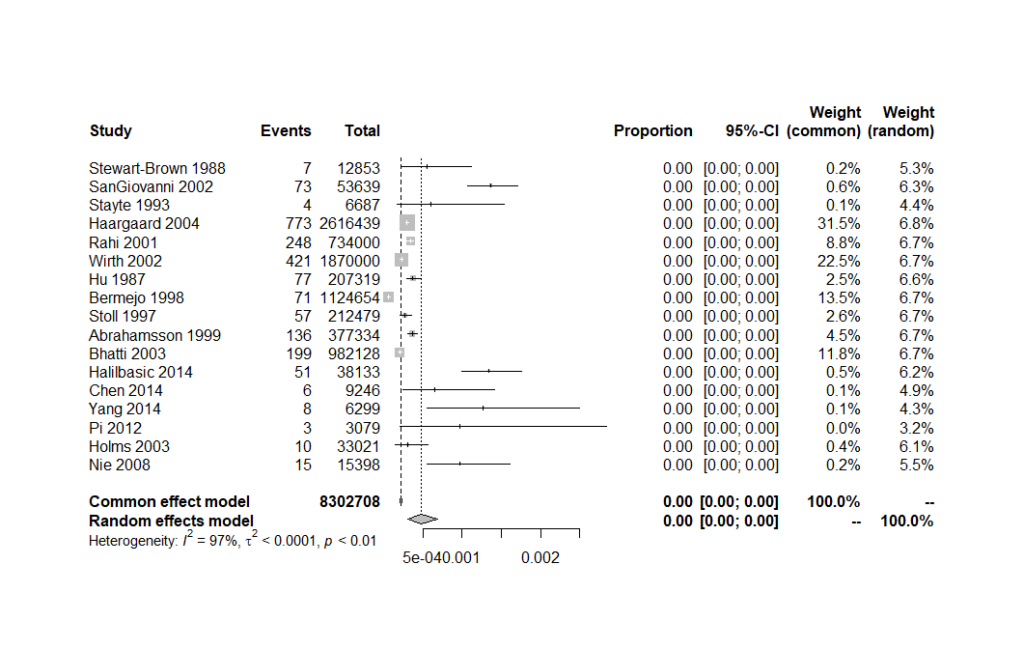
R で割合のメタアナリシスを行う方法
割合のメタアナリシスの方法の解説 割合のメタアナリシスデータ準備 R で割合のメタアナリシスを行う準備 metafor と meta というパッケージをインストールして準備する install.packages(c("metafor", "meta")) library(metafor) library(meta) サンプル... -

SPSS でグループごとの分析を行う方法
SPSS でグループごとの分析を行う場合、どのようにしたらよいか? SPSS でグループごとの分析を行う方法 1: ケースの選択 分析するデータを読み込んだ後、以下の手順で設定する データ → ケースの選択 をクリック 例えば性別 gender が 1 のグループだけ... -

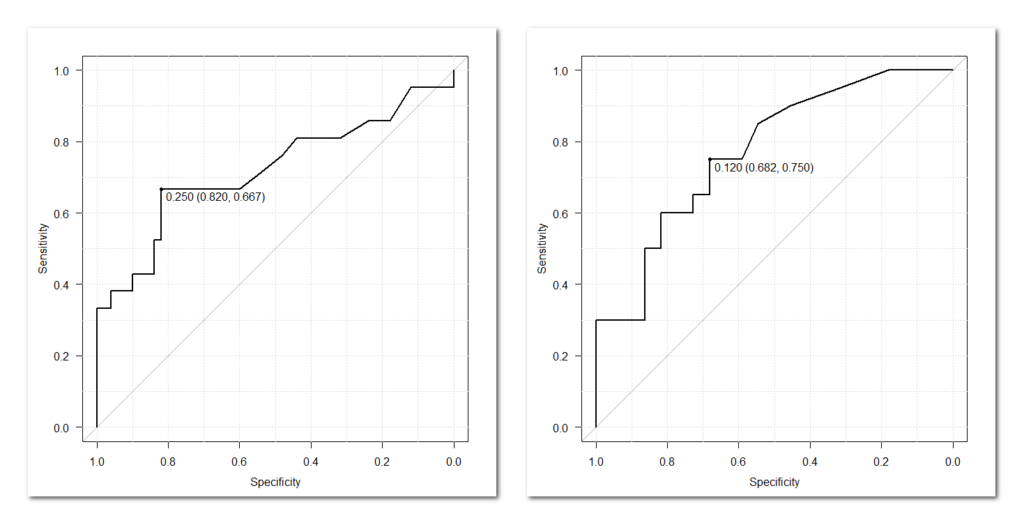
SPSS で ROC 曲線の比較をする方法
SPSS で ROC 曲線を群間比較する方法 2 つの検査値を比較する方法も紹介 ROC 曲線を比較する方法を解説するデータ アウトカムデータ outcome, 検査値データ s100b, 性別データ gender を含むデータ こちらからダウンロードして試してみることが可能 aSAH.s... -

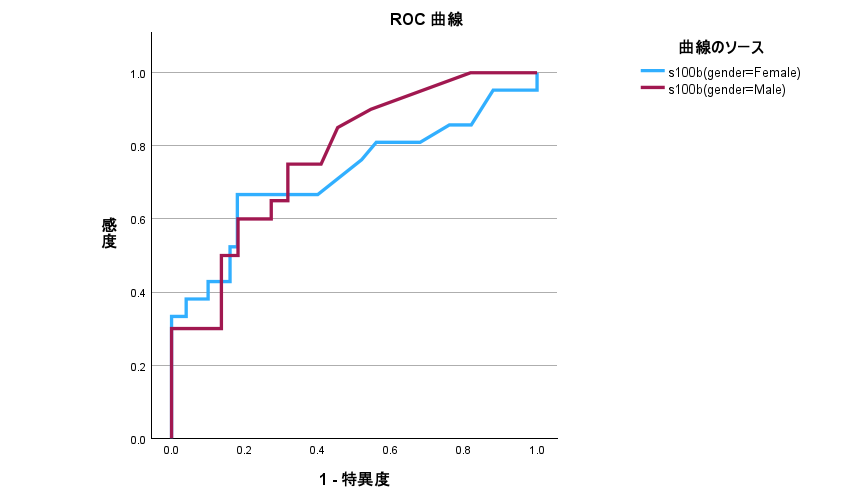
EZR で ROC 曲線の群間比較をする方法
EZR で ROC 曲線を群間比較する方法 ROC 曲線を比較するためのサンプルデータ R の pROC パッケージに含まれる aSAH データセットを使う outcome データで s100b という検査値のカットオフ値を求める gender で female と male の群間比較を行う pROC パッ... -

カイ二乗検定における効果量
カイ二乗検定は、2つのカテゴリカル変数の間に統計的に有意な関連があるかどうかを判断するのに役立つ手法である。しかし、統計的有意性だけでは、その関連性の「強さ」についてはわからない。そこで重要になるのが効果量である。効果量は、群間の差や変数... -

EZR で正規分布していない連続データから 95 % 信頼区間を計算する方法
サンプルの連続データが正規分布していない場合に、平均値の 95 % 信頼区間を計算する方法 正規分布していない連続データが対数正規分布だった場合 正規分布していない連続データを対数変換すると正規分布に見える場合、その連続データは対数正規分布のデ... -

EZR でステップワイズ変数選択を行うときにある変数だけは必ず選択されるようにする方法
ステップワイズ変数選択の際に ある変数だけは残っていてほしい場合の指定方法 ステップワイズ変数選択を EZR で実行する方法 ステップワイズ変数選択を EZR で実行するには、データを読み込んだ後、例えば重回帰のメニューからステップワイズを選択する ... -

対数変換した値の要約値の書き方
対数変換した後の数値の要約値の論文表への書き方 実際、どのように記載されているか 幾何平均を書いている論文 Does the association of the triglyceride to high-density lipoprotein cholesterol ratio with fasting serum insulin differ by race/eth... -

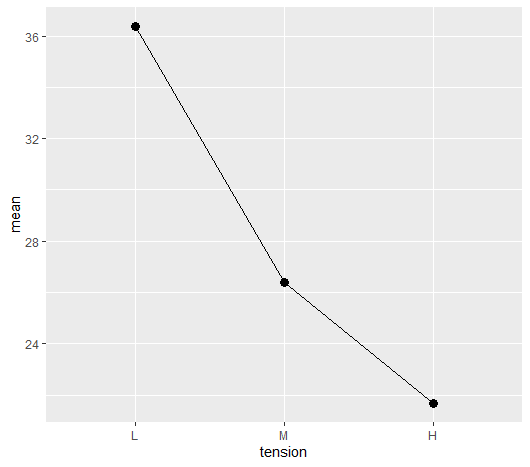
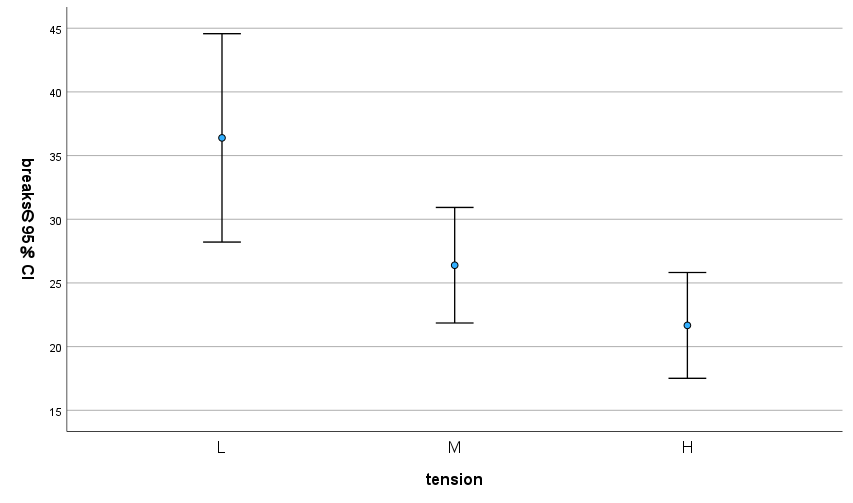
SPSS で分散分析に必要なサンプル数を計算する方法
分散分析のサンプルサイズ計算をSPSSで行う方法 分散分析のサンプルサイズをSPSSで計算する前に効果量を見積もる 分散分析のサンプルサイズをSPSSで計算する際に、必要なのは効果量を見積もること 先行研究の分散分析表を使うとよい 今回は tension の高さ... -

SPSS でダミー変数を作成し重回帰分析でカテゴリ変数を使う方法
重回帰分析で、独立変数にカテゴリ変数を使う方法を解説する。 SPSSでは、ダミー変数を作成しておく必要がある。 ダミー変数とは何か? ダミー変数の作り方は? 重回帰分析をSPSSで行う方法 重回帰分析をSPSSで行う場合、2つの方法がある。 ひとつは、「... -

EZR と R で IPTW ログランク検定を実行する方法
IPTW ログランク検定をEZRとRを使って行う方法。 IPTWとは? IPTW とは、Inverse Probability of Treatment Weights の頭文字語。 日本語では、逆確率重みづけと言う。 交絡因子調整方法の一つ。 詳しくは他の記事も参照のこと。 IPTW ログランク検定とは... -

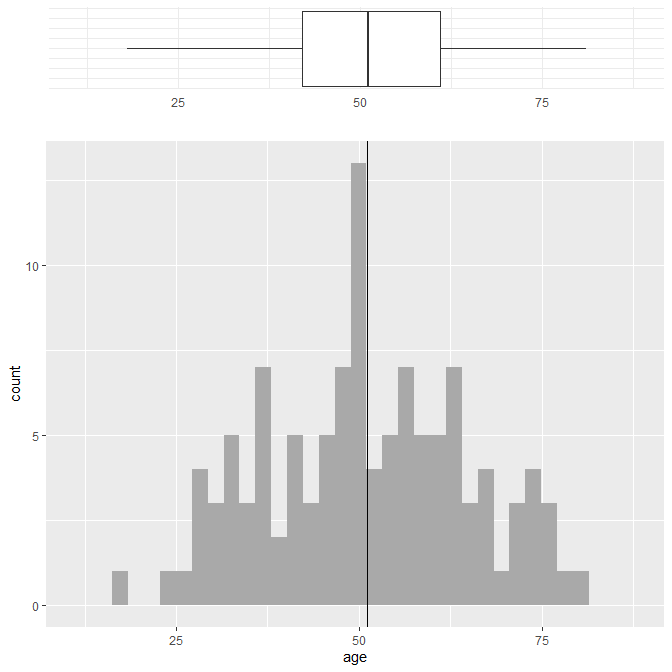
R で ggplot を使ってヒストグラムと箱ひげ図を一つのグラフに書く方法
Rでヒストグラムと箱ひげ図をggplot2 を使って重ねて描く方法の紹介。 Rでヒストグラムをggplot2 を使って描く方法 Rでヒストグラムをggplot2を使って描く方法を紹介する。 まずggplot2 パッケージをインストールして、呼び出しておく。 install.packages(... -

エクセルでカイ二乗検定を行う方法を例題でわかりやすく解説
カイ二乗検定をわかりやすく解説。 エクセルでの計算方法も紹介。 カイ二乗検定とは? カイ二乗検定とは、サンプルのグループ間の「何か」の割合を比較することで、グループの母集団の割合が統計学的に違うかどうかを調べる方法である。 グループ間で何か... -

カテゴリ変数を用いた主成分分析を行う方法
主成分分析をカテゴリ変数が含まれるデータセットで実施する方法を紹介する。 主成分分析をカテゴリ変数で実施可能か? カテゴリ変数でも主成分分析はできるか? 答えはYesである。 SPSSで実施可能である。 ただし、追加のパッケージ (Complex Sample) が... -

脳ネットワーク分析 Brain Network Analysis の簡単な解説
Brain Network Analysisでよく使われている手法について理解したところをまとめてみる。 Brain Network Analysisで登場する用語 Brain Network Analysisで登場する用語は、一般的なネットワーク分析で登場する用語と被るものが多い。 ネットワーク分析の基... -

EZR で箱ひげ図を書くとき色分けする方法
EZR で箱ひげ図を書くにはどうしたらよいか? 色分けするにはどうしたらよいか? EZR で箱ひげ図を書く方法 データを読み込んだ後、グラフと表から箱ひげ図メニューを選択する。 変数のほうで連続データを指定し、群別する変数の枠で群を表すカテゴリカル... -

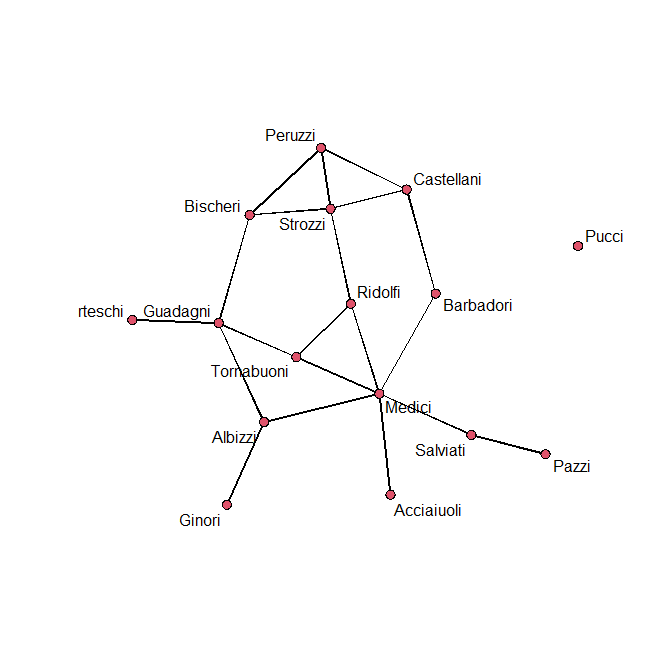
ネットワーク分析の簡単な解説
ネットワーク分析の基礎知識として用語の簡単な解説。 ネットワーク分析とは? ネットワーク分析とは、社会学や通信ネットワークなどの分野で用いられる分析手法である。 脳画像を用いた脳内のネットワーク分析も行われている。 このネットワーク分析は、... -

SPSS と R の主成分分析で軸の回転を行う方法
主成分分析で軸の回転をすることはできるか 主成分分析とは? 主成分分析とは、多数の変数の情報を少数の合成変数に縮約する解析手法である。 たくさん変数があると何がどうなっているかわからないが、それら変数同士の相関関係を活用して、代表的な方法と... -

MMRM に必要なサンプルサイズ計算を行う方法
MMRMは、Mixed Model with Repeated Measuresの略である。 反復測定の連続データを線形混合モデルで解析することを意味している。 この試験・研究デザインのとき、サンプルサイズ計算はどのようにしたらよいか? MMRMのサンプルサイズ計算サイト 以下のサ... -

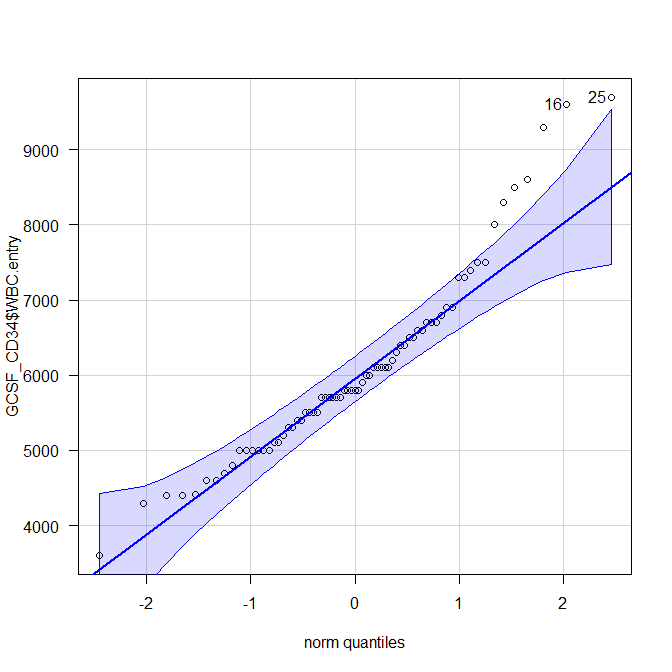
正規性の確認に用いる QQ プロットの解説
正規性の確認は、検定は不要で、グラフで確認すればよい。 ヒストグラムが一番簡単な方法だが、もう一つグラフで確認する方法がある。 それがQQプロットだ。 QQプロットとは何か? QQプロットの前に 正規性とは? 統計解析の検定において正規性が条件であ... -

R でネットワーク図を書く方法
R におけるネットワーク分析のパッケージ network の簡単な使い方。 network パッケージのインストール まず統計ソフトRにパッケージをインストールして呼び出す。 install.packages("network") library(network) 準備するデータ ネットワークのつながりあ... -

対数変換された説明変数のハザード比を真数の説明変数のハザード比に変換できるか
対数変換した説明変数の単位数当たりのハザード比を、真数に戻した説明変数の単位数当たりのハザード比に計算できるだろうか? 論文で発表された数値を使うメタアナリシスを行うことはできるか? つまり、生データがない場合である。 どういう状況か? 例... -

正準相関分析をわかりやすく解説
正準相関分析とは、どんな分析で、どんなときに使うのか? 正準相関分析とはどんな分析か 正準相関分析 canonical correlation analysis は、一言で言うと、2つの変数群を2つの合成変数にまとめ、その合成変数間の相関係数を最大にする方法である。 正準...