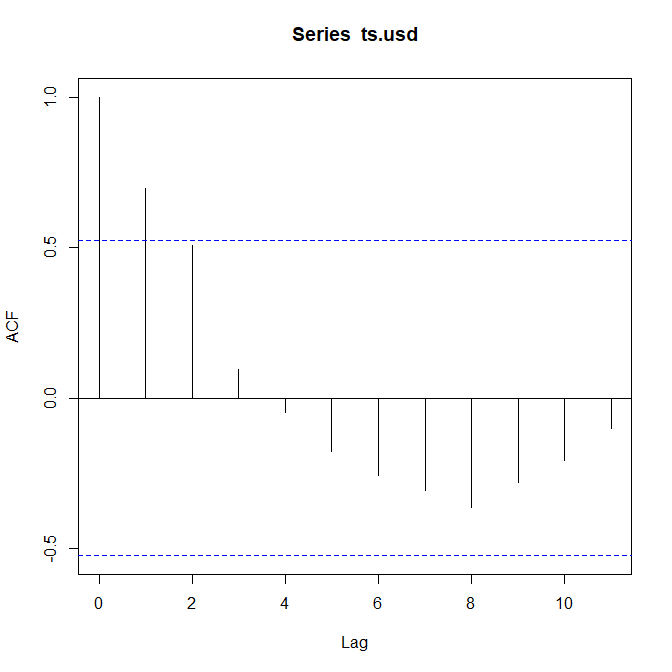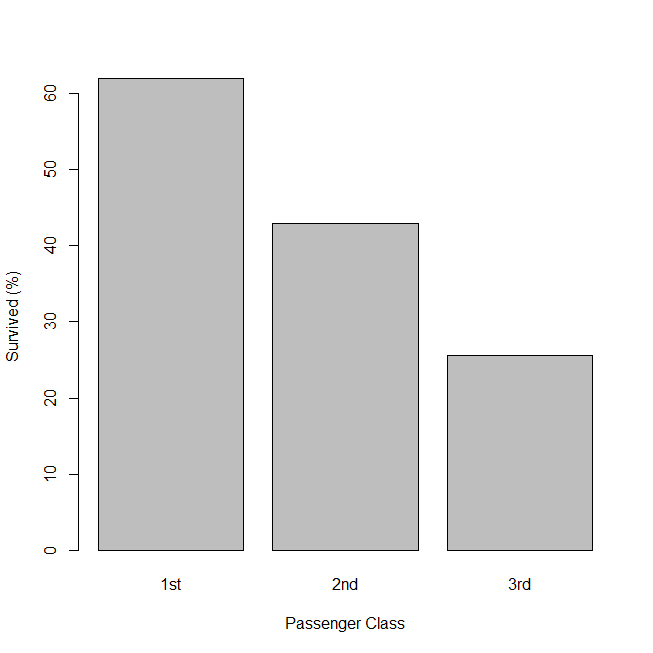-

SPSS で平均値の折れ線グラフを書く方法
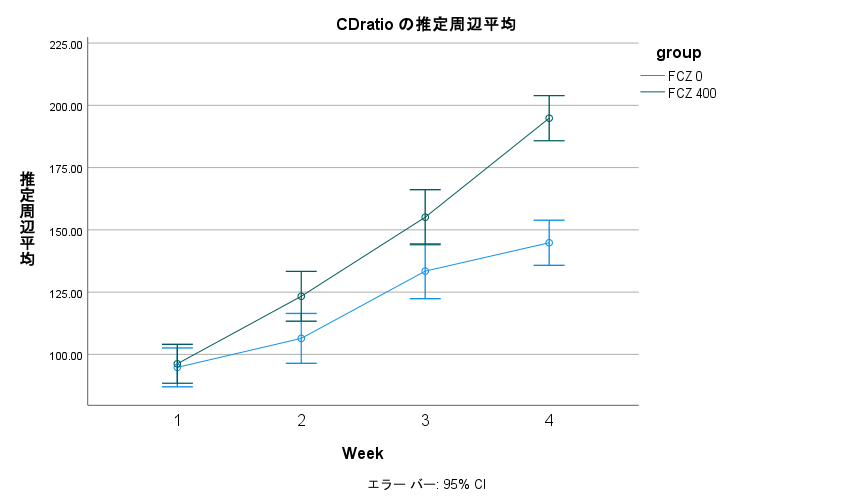
平均値の折れ線グラフとは、経時的な測定によって得た測定値の平均値を線で結んだグラフを指している。 SPSS で書く方法の解説。 SPSS で平均値の折れ線グラフを書くデータ準備と解析準備 まず、一人一行で、反復測定を列方向に並べたデータを準備する。 ... -

多重代入法で必要な補完データセット数
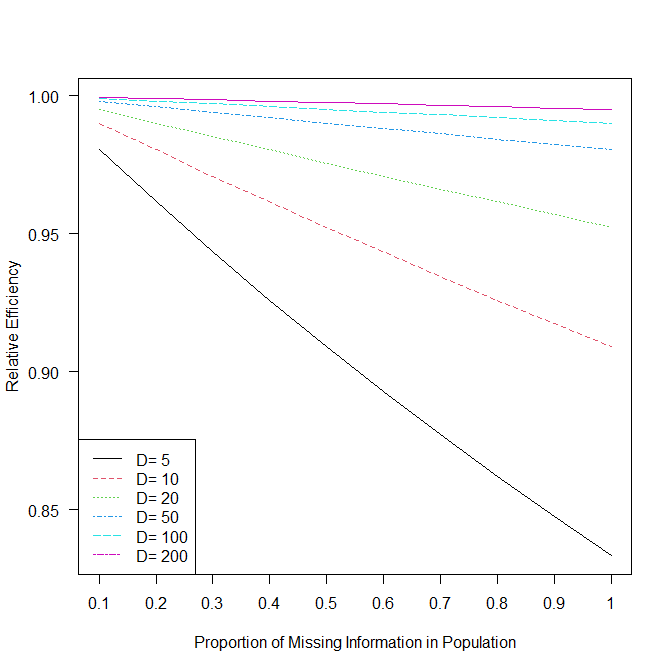
欠測値があった場合、対処する方法がいくつかある。 そのうちの一つが多重代入法である。 多重代入法で作成すべき欠測値補完データの数はいくつがよいのか? 多重代入法で作成するデータセットはいくつがよいと言われているか? 多重代入法の提案者Rubinは... -

SPSS で適合度検定を実行する方法
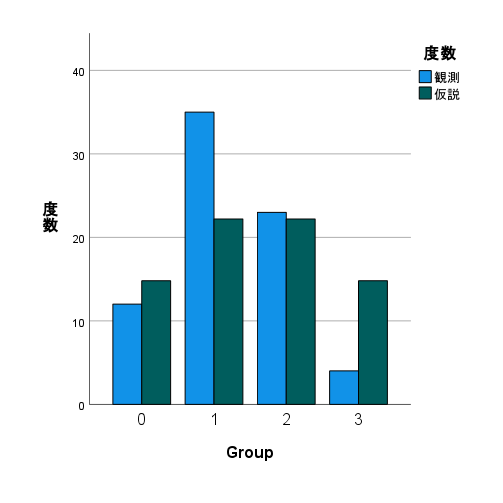
SPSS で理論分布・期待分布・母集団の分布に適合しているかどうかの適合度検定を行う方法 適合度検定とは? ここで言う適合度検定とは、理論分布・期待分布・母集団の分布に適合しているかどうかを検定するものを言っている。 適合度検定というような名称... -

SPSS のカイ二乗検定で3つ以上のカテゴリがある場合の多重比較の方法
カイ2乗検定で3つ以上のカテゴリがある場合、カテゴリ同士の比較はどうやればよいか? その場合は、3群以上の割合の比較と考えればよい。 例えば、SPSSで3群以上の割合を比較するには、z検定を使って繰り返し検定し、必要に応じ、Bonferroni調整を行... -

傾向スコアマッチング回帰分析 簡単な説明
傾向スコアマッチングは、ある因子についてランダム化していなかった観察研究データにおいて、そのある因子以外は同様にした2つのグループをマッチングで作成する方法である。 目的変数が連続量の場合でも利用可能だろうか? 傾向スコアマッチングとは? ... -

AICとBICの違いは何か?統計解析での特徴比較
統計モデルの当てはまりの指標である、AICとBIC。 違いは何か? AICやBICとは何か? AICは、Akaike's Information Criterion 赤池情報量規準の頭文字語、BICは、Bayesian Information Criterion ベイズ情報量規準の頭文字語である。 AICもBICも予測性能に... -

決定係数の目安 ― 決定係数 R 2 乗値はいくつならよいか?
重回帰分析の当てはまりの良さを示す決定係数。 決定係数はR2乗値ともいう。 決定係数の目安はあるのだろうか? ゼロから1の範囲をとるわけだが、いくつなら良いのか? 決定係数の目安は? 決定係数は、重回帰分析の当てはまりの良さ、適合度の良さとして... -

クラスカルウォリス検定とマンホイットニーの U 検定は何を検定しているか
ノンパラメトリック検定の場合、平均値の差を使っているわけではないが、では何の検定なのか? クラスカルウォリス検定は何の差を見ているのか? クラスカルウォリス検定は、3群以上の連続量を比較するノンパラメトリック検定である。 クラスカルウォリス... -

EZR でオッズ比の計算に必要なサンプルサイズを計算する方法
オッズ比のサンプルサイズ計算の方法 オッズ比計算のためのサンプルサイズ計算・検出力計算のための準備 EZRにepiR パッケージをインストールする。 Rスクリプト窓にinstall.packages("epiR")と書いて実行をクリック。 ダウンロード元を選ぶ(2024 年 10 ... -

JMP のノンパラメトリックな多重比較の使い分け
JMPでノンパラメトリックのDunnett検定として、Steel検定と併合順位のDunn検定がある。 どちらを選択すべきか? JMPで利用可能なノンパラメトリックなDunnett検定としての検定 2 つ 統計ソフトJMPでは、コントロール群と複数の実験群を多重比較するDunnett... -

SPSS のロジスティック回帰で方程式中にない変数とは何か?
SPSSでロジスティック回帰を実行すると方程式中にない変数という表が現れる。 あれはいったい何なのだろうか? SPSSでロジスティック回帰に説明変数を投入すると SPSSではまず定数項だけでロジスティック回帰を実施する。 変数を投入したモデルと比較する... -

SPSS でロジスティック回帰をするときに投入変数をだんだん増やす方法
SPSSでロジスティック回帰を実行するときに調整変数をだんだん増やしていきたい時がある。 そんなときはブロックを使うと便利。 SPSSでロジスティック回帰をするときに独立変数をブロックに分けて投入する方法 まず、分析 → 回帰 → 二項ロジスティック を... -

R で分散の信頼区間を計算する方法
分散の信頼区間を R で計算する方法の解説。 分散の信頼区間を計算するスクリプト Rスクリプトは以下の通り。 var.interval <- function(data, conf.level=0.95){ df <- length(data) - 1 chilower <- qchisq((1-conf.level)/2, df) chiupper <... -

EZR の出力をエクセルに貼り付ける方法
EZRの出力は固定長といってスペースできれいに整えられている。 Excelのテキストファイルウィザードを使用すればきれいに貼り付けることができる。 EZRの出力をエクセルにきれいに貼り付ける方法 EZRを機能を使ってきれいに出力する方法は下記のブログ記事... -

EZR の 2 群の比率の差の信頼区間計算で小数点以下の桁を増やす方法
EZRで2群の比率の差の信頼区間を求めると小数点以下3桁に丸められた数値が出力される。 小数点以下の桁数を増やす方法。 EZRで2群の比率の差の信頼区間を求める 「統計解析」→「名義変数の解析」→「2群の比率の差の信頼区間の計算」メニューを使って、計... -

EZR で出力結果をエクセルに貼り付けたりファイルに出力したりする方法
EZRの出力をきれいにエクセルに貼り付ける方法があるか? エクセルで開けるファイルに出力する方法があるか? EZRの出力結果をきれいにエクセルに貼り付ける方法 EZRで分割表の出力結果をエクセルに貼り付ける方法を紹介する。 まずEZRで分割表を計算する... -

EZR で比例ハザード性を二重対数プロットで確認する方法
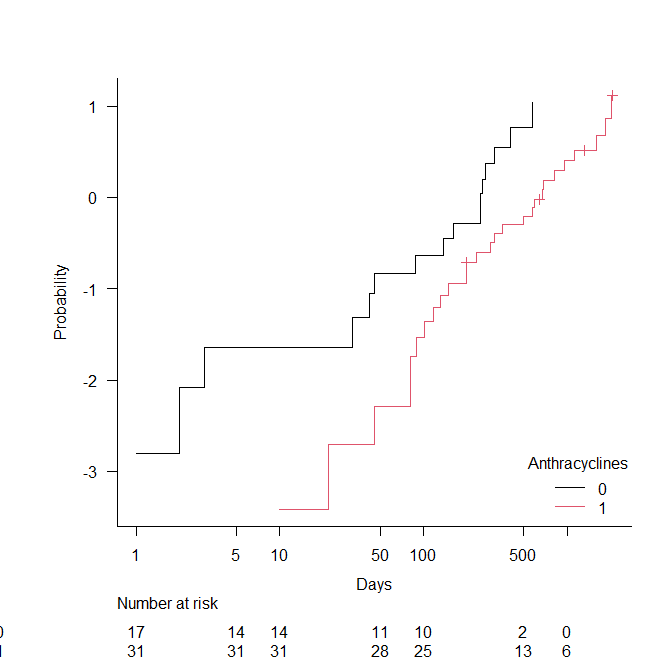
Cox 回帰で必要な、比例ハザード性を確認する方法の解説 比例ハザード性を二重対数プロットで確認する方法 EZRで比例ハザード性を確認する方法の一つ目として、グラフで確認する方法がある。 二重対数プロット( Complementary log-log plot )というもの... -

R で Box-Cox 変換を行う方法
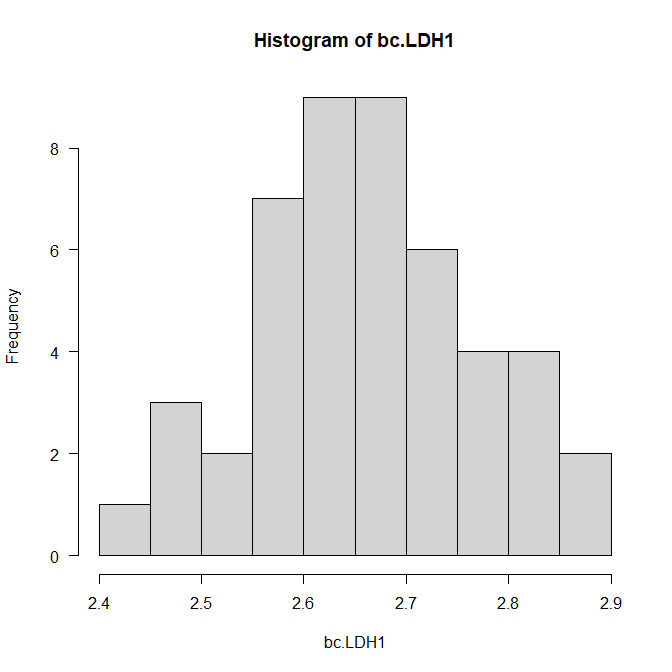
連続量を何らかの方法で正規分布に近づける方法はいくつかある。 ここではBox-Cox変換の方法をまとめてみた。 R で Box-Cox変換を行う実例 まず、car パッケージを呼び出す。 library(car) car パッケージの中の、powerTransform()とbcpower()を使って変換... -

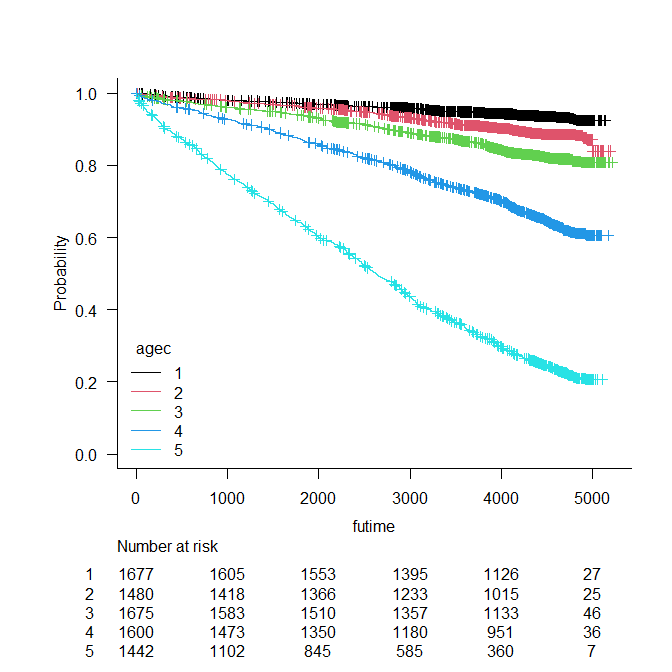
EZR で書いたカプランマイヤー曲線グラフの横軸を変更する方法
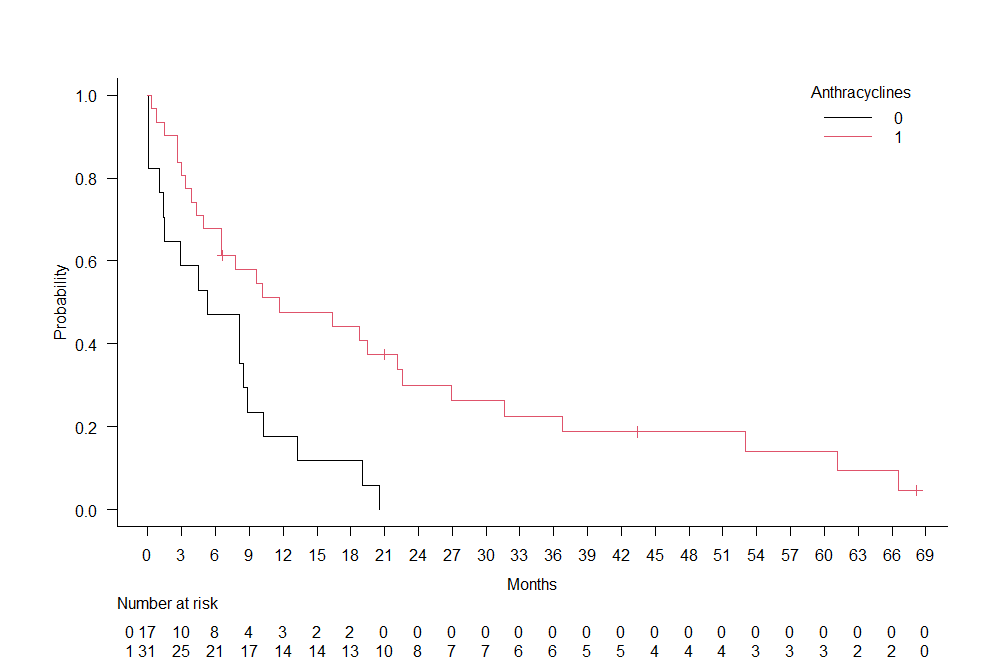
EZRでカプランマイヤー曲線を書いた後に、横軸を調整する方法 EZRでカプランマイヤー曲線を描いているスクリプト部分を特定する EZRで生存期間解析、ログランク検定からカプランマイヤー曲線を描く。 EZRでカプランマイヤー曲線を描く方法は、以下の動画を... -

EZR で書いたグラフを別のソフトウェアで編集する方法
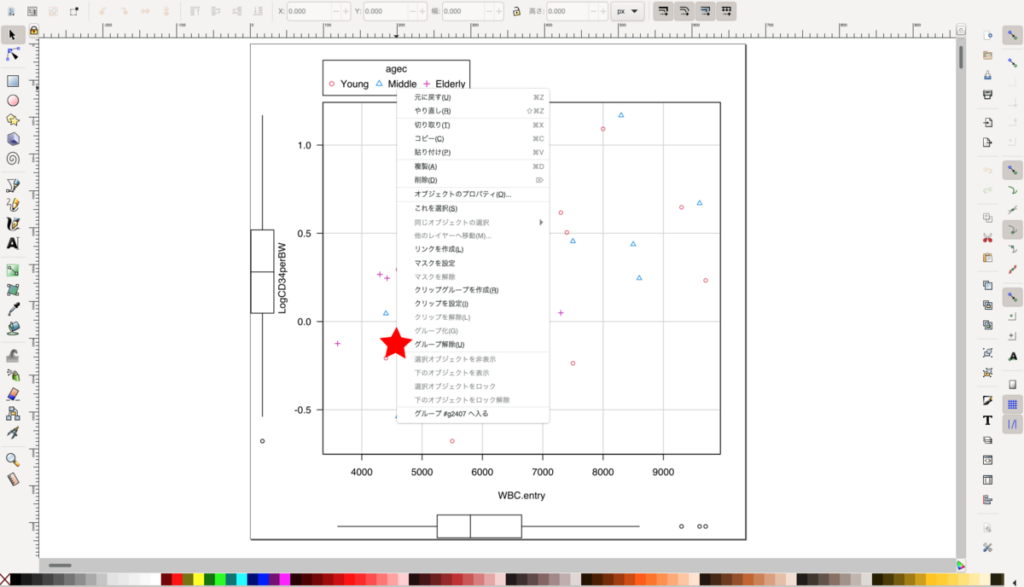
EZRでグラフを描いたあと、一部文字を消したり、文字を加えたり、図形を加えたり、ちょっとした修正を行う方法 EZR のグラフを編集する方法 ― Mac の場合 Mac版のEZRでグラフを描いた場合、その後に修正するときは、どうしたらよいのか? グラフはPDFの形... -

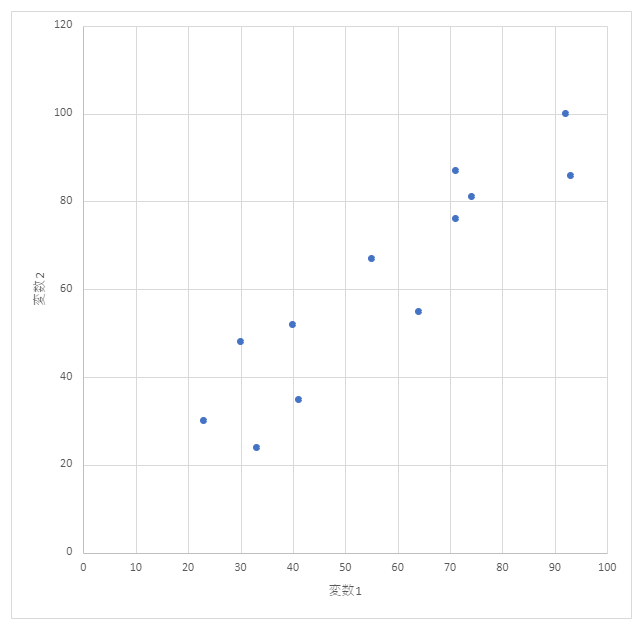
EZR で散布図を書くときに色分けする方法と点の形を変更する方法
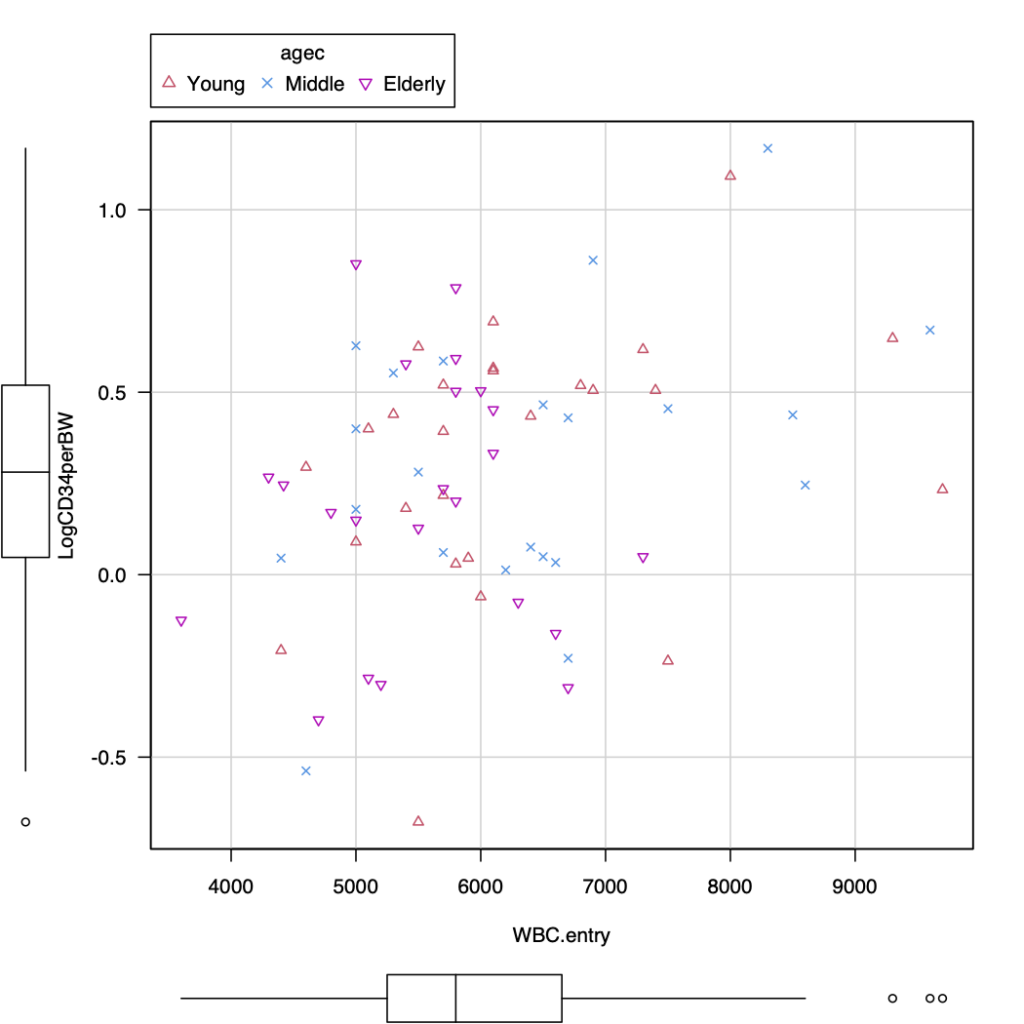
EZRで散布図を書く方法を解説。 色分けや点の形を変えて、グループ別に描画する方法を解説する。 EZRで散布図を色分けしてグループ別に書く方法 EZRを起動して、データを読み込んだら、「グラフと表」から「散布図」を選択する。 x軸の変数とy軸の変数を... -

SPSS で偏相関係数計算に必要なサンプルサイズを計算する方法
お互いにある変数と相関がある変数同士の相関係数を算出する場合、お互いに相関がある変数の影響を排除したうえでの相関を検討したいことがある。 そのようなときに使う方法が偏相関係数だ。 偏相関係数を算出する試験デザインを考える際に、サンプルサイ... -

EZR のフィッシャーの正確検定で 95 %信頼区間が 1 をまたいでいるが統計学的有意である場合の対処法
オッズ比の95%信頼区間が1をまたいでいないことと、有意水準5%で統計学的有意であることはイコールである。 しかし、EZRでフィッシャーの正確検定を実施すると、有意確率が5%未満であるにもかかわらず、オッズ比の95%信頼区間が1をまたいでいること... -

EZR のフィッシャーの正確検定で計算されるオッズ比の注意点
EZRのFisherの正確検定の関数でオッズ比を計算すると、通常の手計算で計算できるオッズ比と異なる数値が計算される。 これはなぜなのか? EZRのFisherの正確検定を使わないオッズ比の計算 オッズ比は、通常は以下のような分割表だった場合、$ \frac{a/c}{b... -

EZR のフィッシャー正確検定でオッズ比の信頼区間のパーセントを変える方法
EZR のフィッシャーの正確検定でオッズ比の信頼区間のパーセントを変える方法。 EZRでフィッシャーの正確検定を行うには? EZRでフィッシャーの正確検定(Fisher’s Exact Test)を行うには、使用するデータを読み込んでから「統計解析」から「名義変数の解... -

EZR で書いたカプランマイヤー曲線の凡例を調整する方法
EZR のグラフの凡例を移動したり、軸の範囲を広げたりして、調整する方法 EZR でグラフを書く方法 総論 ヒストグラムや散布図など一般的なグラフは、「グラフと表」から選択する。 たいていのグラフはこのメニューから描ける。 カプランマイヤー曲線を描き... -

EZR でフォント・フォントサイズの変更と EZR 自動起動の設定方法
EZR のフォントやフォントサイズを変更するにはどうやったらいいか。 EZRの起動時フォントなどはオプションから設定する EZRの起動時フォントなどはメニューバーの「ツール」→「オプション」から変更する。 EZRのオプション画面のフォントタブでフォントと... -

尤度とは?わかりやすく解説
読み方も意味しているところも分かりにくい尤度(ゆうど)。 わかりやすく解説。 尤度と似ている確率とは何か? まず尤度は確率に似ているものだが、確率とは違う。 まず確率とは何かを、尤度との対比になるような説明を紹介したい。 統計学で考える場合、... -

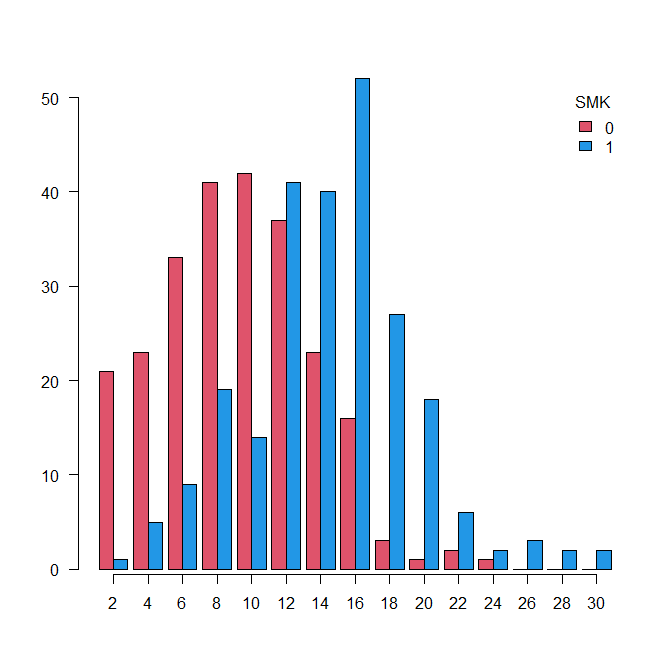
EZR で書いたヒストグラムの色を変える方法
EZR でヒストグラムを書いて、色を変える方法 EZR でヒストグラムをグループ別にカラーで描いてみる KTSND という連続データと SMK というカテゴリカルデータを用いて、ヒストグラムを書いてみる EZRのメニュー「グラフと表」から「ヒストグラム」を選択。... -

R EZR エクセル SPSS で相関係数の計算・検定・必要なサンプル数を計算する方法
相関係数の計算に必要なサンプル数はいくつか? 相関係数の検定との関係から紹介。 相関係数のサンプル数計算の前提となる検定の計算方法 相関係数の検定は、母集団の相関係数、母相関係数(ぼそうかんけいすう)がゼロかどうかの検定である。 通常はt分... -

R で時系列データの自己相関を計算する方法
自己相関を時系列データで計算する方法を解説した。 時系列データとは? 時系列データは、時間とともに計測したデータのこと。 毎日のデータ、毎月のデータ、四半期のデータ、毎年のデータというような定期的な時間で取得したデータのこと。 このデータを... -

R で分割プロット分散分析に必要なサンプルサイズを計算する方法
分割プロット分散分析のサンプルサイズ計算の方法。 分割プロット分散分析とは? 同じ対象者のある指標を反復して測定したときのデータを分析したいことがある。 対象者をいくつかの群に振り分けて比較したいことが多い。 ここでは、この解析方法を「分割... -

R で分散分析に必要なサンプル数を pwr.anova.test() で計算する方法
分散分析のサンプルサイズ計算を統計ソフトRで行う方法を解説。 分散分析は三群以上の平均値を比較する分析方法。 少なくともどれか一つの群がほかの群とは異なることを証明するための分析方法だ。 分散分析のサンプルサイズ計算を行うために必要なデータ ... -

R と SPSS でウェルチの t 検定を実行する方法
ウェルチの t 検定は、2 群が等分散でも等分散でなくても使える t 検定 R と SPSS での実行方法 ウェルチの t 検定とは? ウェルチ (Welch) の t 検定は、二つのサンプルの母分散が等分散とは仮定できないときにも適切に比較できる平均値の差の検定だ。 等... -

おすすめ統計本―医学統計を中心に
統計ER的おすすめ統計本のリストアップ 何らか参考になれば 医学統計学 医学への統計学 基本的なことがきちんと書いてある本。しっかり勉強するのにおすすめ。サンプルサイズ計算についてもかなり充実している。 医学への統計学 (統計ライブラリー) 医学デ... -

R でサポートベクターマシンを実行する方法
サポートベクターマシンを R で実装する方法について。 サポートベクターマシンとは? サポートベクターマシンについては、過去記事参照。 サポートベクターマシンを R で実装するのに必要なパッケージ e1071パッケージを使う。 まず最初一回インストール... -

R で割合の差の検定に必要なサンプルサイズを計算する方法
割合の差の検定のサンプルサイズ計算を R で行う方法、エクセルで行う方法 割合の差の検定のサンプルサイズ計算 R の関数を使って 統計ソフトRには、power.prop.test()という関数が用意されていて、簡単に計算できる。 第1群が50%(0.5)、第2群が75%(0.75)... -

R で クロッパーピアソンの割合の信頼区間を計算する方法
正規分布近似を用いた信頼区間とClopper-Pearson 信頼区間を計算する方法。 割合の区間推定(正規分布近似を用いた簡易的な方法) 割合の分散は、割合をp、サンプルサイズをnとすると、 $$ \frac{p (1 - p)}{n} $$ で計算できる。 標準誤差はその平方根で... -

R のパッケージを source からインストールする方法
R はパッケージを追加すると新しい機能が追加できる。 その方法もとても簡単だ。 R のパッケージの追加方法として source からインストールする方法があるので、その解説。 R のパッケージを source からインストールする方法 R のパッケージは、Windows用... -

R で時系列データ分析を行う方法
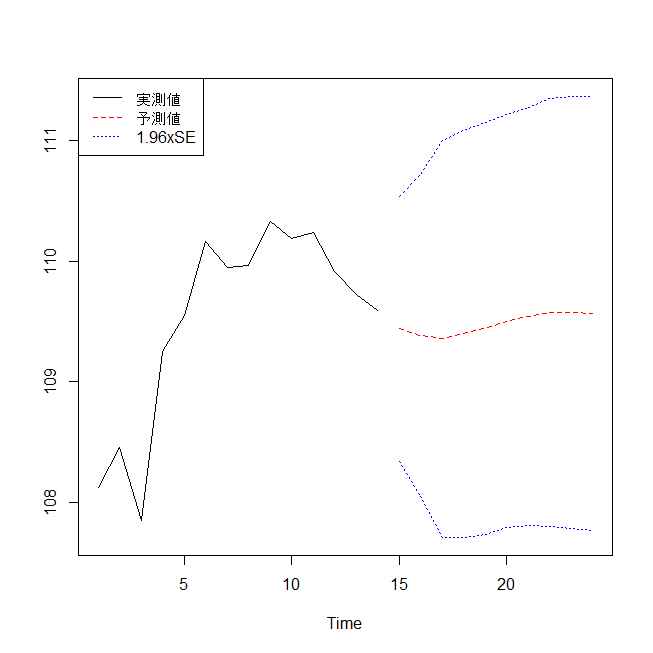
R で時系列データを分析するための基礎的な方法の解説。 時系列データとは何か? 時系列データとは、日時のデータと値のデータのペアのこと。 例としては、 四半期ごとの売上高。 毎月の経費。 週当たりの納入量。 毎日の株価・ドル円レート。 など。 こう... -

R で多重比較に必要となるサンプルサイズを計算する方法
多重比較のサンプルサイズ計算を R で行う方法 ボンフェローニ型 多重比較のサンプルサイズ計算 Bonferroni(ボンフェローニ)型多重比較とは、比較する数で有意水準を割って、割った有意水準より小さい有意確率の場合、統計学的有意と考える方法。 三群あ... -

R で 5 年生存率から逆算で生存期間中央値を求める方法
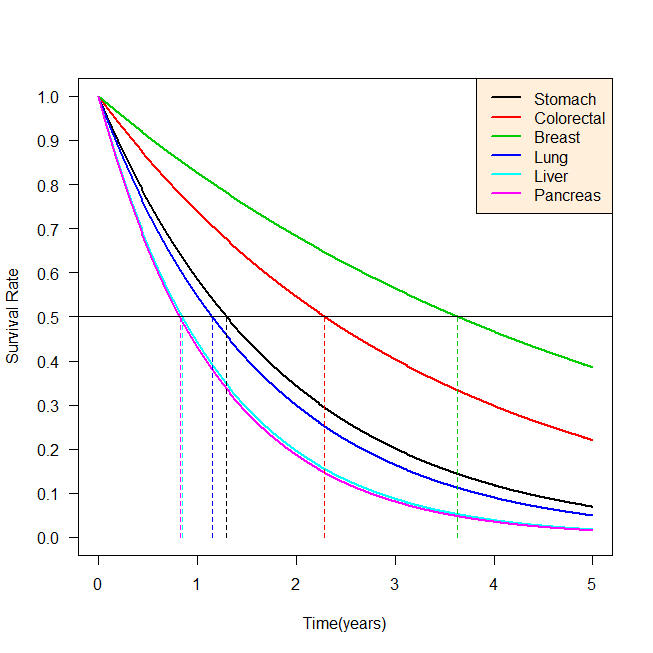
がん患者さんの生存期間中央値を5年生存率から逆算で求めるにはどうしたらよいか? R で計算する方法。 5 年生存率から逆算で生存期間中央値を求める計算式 生存確率は、一般論として指数関数で近似できる。 実際には、がんの治療後すぐになくなったり、数... -

R でロジスティック回帰分析と傾向検定・多重比較を行う方法
R に組み込みのタイタニック号の生存・死亡データで、生存・死亡に関するロジスティック回帰分析と、独立変数の多重比較を実行してみる。 解析するタイタニック号の生存・死亡データの確認 解析するデータは、carData パッケージの TitanicSurvival という... -

R でロジスティック回帰を行う方法
タイタニック号は、1912年4月14日の夜、氷山に激突し、北大西洋の底に1,500名以上の命と一緒に沈んだ。 乗客乗員の生存・死亡のデータを用いて、ロジスティック回帰分析を実行してみる。 タイタニック号の生存・死亡データはどこにあるのか? R はインスト... -

偏相関係数を計算したいときに考えること
偏相関係数について。 順位相関係数は偏相関係数が計算できるか。 偏相関係数が計算したい場面 新規の検査値Aと既存の検査値Bの関連性を検討したい。 nは40例程度。 解析するに当たり、患者背景が問題になると思っている。 既存の検査値 Bと身長が関連する... -

R で相関係数と偏相関係数の違いについて ピアソンとスピアマンの両方について
相関係数は、相関関係の強さを示す指標。 一方が大きいときにもう一方が大きければ、正の相関関係で、相関係数は1に近い。 一方が大きいときにもう一方が小さい場合は、負の相関関係で相関係数は-1に近い。 では、偏相関係数とは何か? 違いは何か? 偏相... -

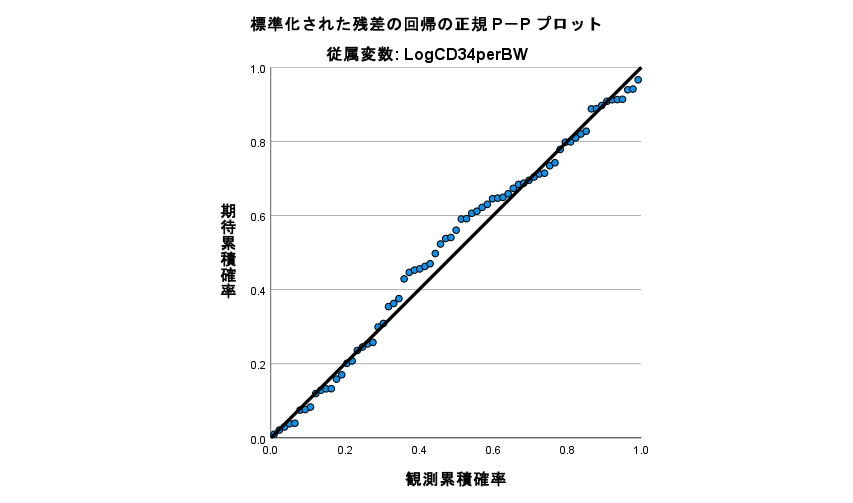
R と SPSS で重回帰分析の残差が正規分布であるのを確認する方法
回帰分析をする際に、説明変数や目的変数が正規分布をしていないことで悩んでいる人は多い。 悩むところはそこじゃない。 重回帰分析では、残差が正規分布している必要がある。 重回帰分析の前提は何か? 重回帰分析の前提は4つある。 独立性(データそれ... -

t 検定と分散分析と回帰分析は同じことをしている
分散分析と回帰分析とt検定は同じものである。 これがわかれば、重回帰分析(共分散分析)が交絡因子調整した群間比較に使われる理由がわかるだろう。 t検定は回帰分析でもできるし、分散分析は二群でもできる ここで、t検定は、いわゆる t 検定のこと... -

多重共線性を回避する方法
多重共線性(たじゅうきょうせんせい)があるかどうかを確認する必要があるとはよく聞くが、確認して多重共線性があった場合はどうすればよいのか? 多重共線性とは?多重共線性はなぜ問題なのか?そして多重共線性を回避するにはどうすればよいか?につい... -

SPSS で Cox 回帰における変数選択の方法とカテゴリ変数のハザード比の求め方
SPSS で Cox 回帰をする際の変数選択の方法とカテゴリ変数の設定の方法の解説 SPSS で Cox 回帰を行う例 SPSSでのCox回帰を行う例は以下の通り。 心臓カテーテル治療(PCI)を何度も経てから冠動脈バイパス術 (CABG) を行う患者の長期成績は不良かというテ... -

多変量解析の変数選択は統計的にどうやるのか
多変量モデルの変数選択について、悩まない人はいない。 どの変数を採用してどの変数を採用しないのか。 明確な基準はあるのか? 想定している多変量モデルは? 多変量モデルは、多変量解析のモデル(もしくは型)を指している。 独立変数に多数の変数を使... -

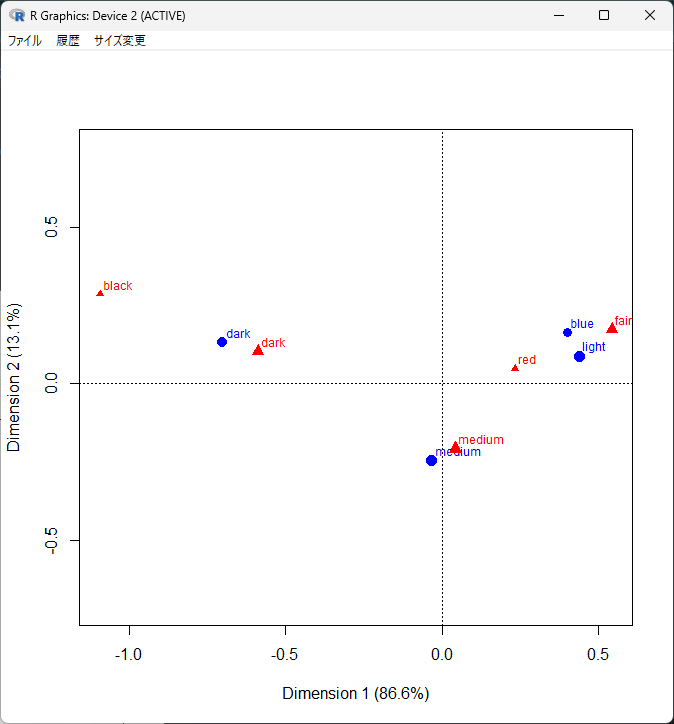
R でコレスポンデンス分析の計算を Step by Step で確認する
コレスポンデンス分析(対応分析とも言う) は、大きな分割表に集計されたデータを見やすくする分析方法。 二次元 つまり X軸とY軸に変換して、散布図にして傾向を見る。 コレスポンデンス分析とは? コレスポンデンス分析とは、対応分析とも呼ばれ、分割... -

階層的クラスター分析で使われるウォード法とは? わかりやすく解説
階層的クラスター分析のクラスター化の方法のウォード法とはどういう方法なのか? クラスター化とは? 階層的クラスター分析はクラスター化をしていく。 クラスター化とは何か? 階層的クラスター分析では、最初にJaccard係数等の指標で、単語同士の「距離... -

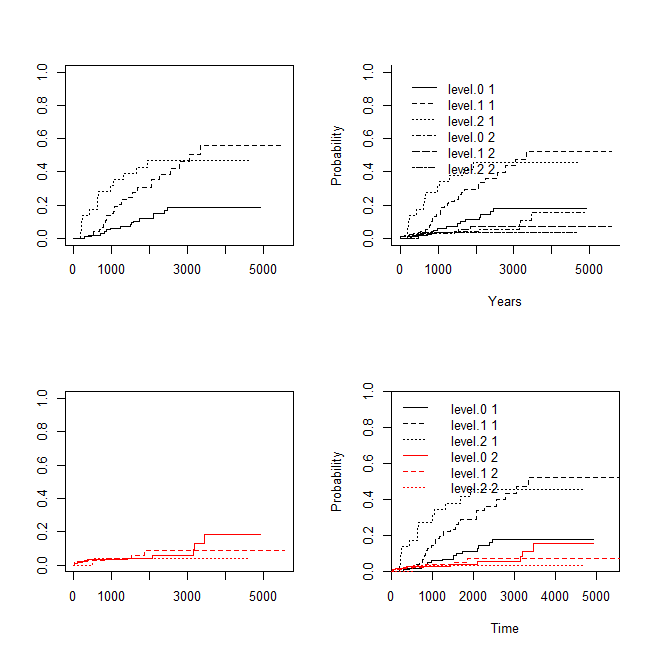
R で競合リスク回帰を実行する方法
競合リスク回帰とは、共変量調整をした競合リスク分析の方法。 競合リスク回帰の前に競合リスクとは? 競合リスクについては、以下を参照。 競合リスク回帰の種類 競合リスク回帰モデルには四つ考えられる。 絶対リスク回帰 Absolute Risk Regression ロジ... -

R で競合リスク分析 Gray 検定を行う方法
競合リスクとは何か? Gray 検定の実行方法 競合リスクとは? 再発がエンドポイントであったが、再発する前に死亡してしまったので、観察できなかった。 脳梗塞の発現がエンドポイントだったが、先に肺炎でお亡くなりになり、観察できなかった。 このよう... -

R で生存時間データを分析する方法
Coxの比例ハザードモデル(コックスの比例ハザードモデル、Cox回帰、コックス回帰など表示・呼び名はたくさんあるが皆同じものを指している)は、生存時間とイベントデータを多変量解析できる統計モデルだ。 注目したい要因が、他の要因と相関があり、また... -

R でログランク検定を行う方法
ログランク検定とは、生存時間解析で、二群以上のグループがある場合に、グループ間で統計学的に差があるかを検討する方法。 R での方法を解説。 R でログランク検定をする場合の関数は? R でログランク検定をする場合、survival パッケージのsurvdiff()... -

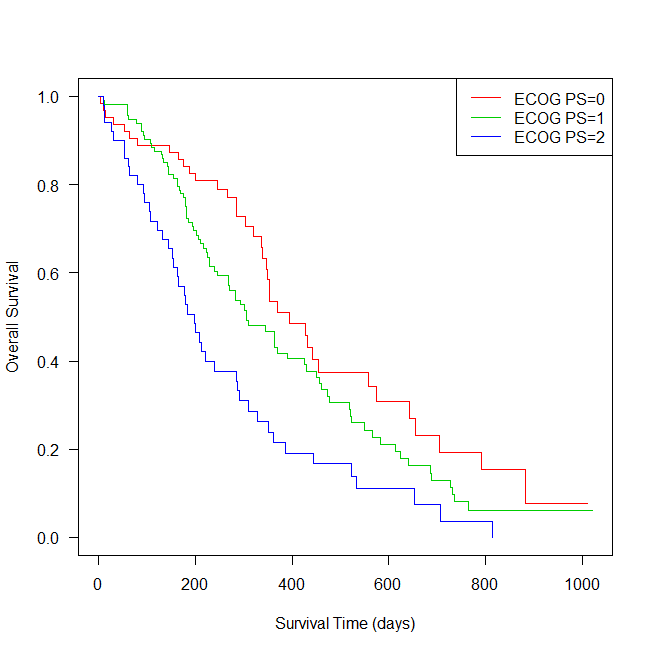
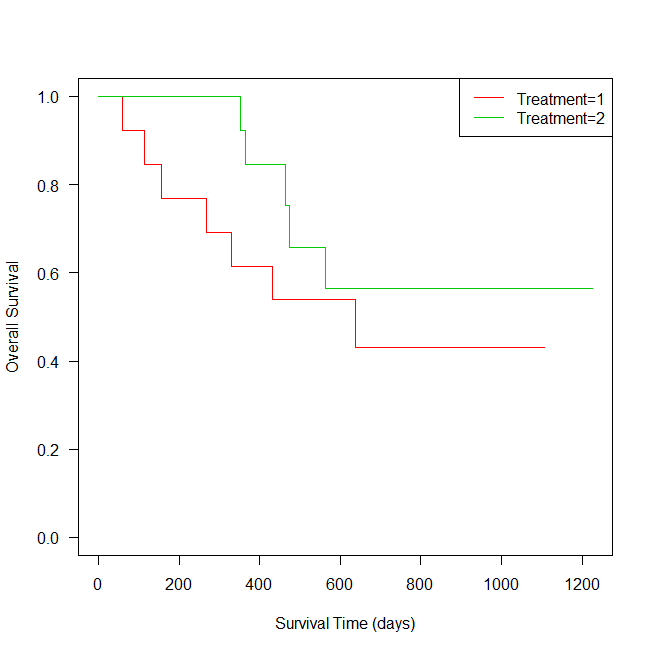
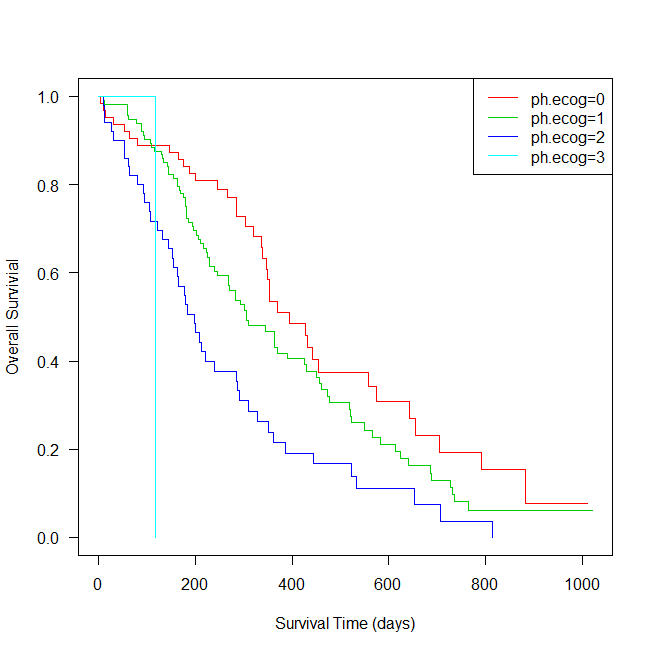
R でカプランマイヤー曲線をグループごとに書く方法
Rでカプランマイヤー曲線を書く方法の紹介。 survfit を使ったグループごとの曲線の書き方。 Rでカプランマイヤー曲線を書くためのサンプルデータ カプランマイヤー曲線を書くためのサンプルデータは、survival パッケージの lung を使う。 これは、North ... -

Jaccard係数とは?― クラスタリングや共起ネットワークの類似度の指標
Jaccard 係数は集合の類似度を表す指標で、テキストマイニングでは、文章と文章の類似度=距離を表す指標になる。 Jaccard係数を少し詳しく解説。 Jaccard係数とは? Jaccard 係数とは、植物学者 Paul Jaccard が考案した集合の類似度を測る指標のこと。 ... -

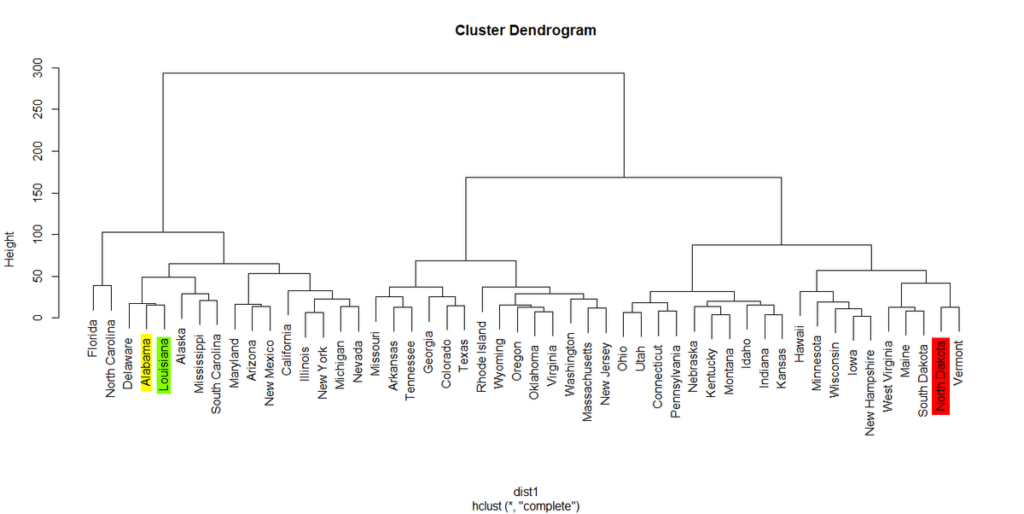
R で階層的クラスタリングを行う方法
R で階層的クラスタリングを行う方法。 階層的クラスタリングとは さまざまな特徴を持った集団、たとえば米国50州を、特徴が似ている似ていないで近い・遠いを表現して部分集団(クラスター)に分けることを言う。 以下も参照のこと。 階層的クラスタリン...