交互作用は文脈によって意味が異なるので意味合いを確認したほうが良い

2022年7月15日2024年9月23日

どうやら「交互作用」と言ったときに、何を指すかは、人それぞれのようだ。

＞＞もう統計で悩むのは終わりにしませんか？

↑期間・数量限定で無料プレゼント中！

交互作用という言葉の帰納的解釈

ウェブサイトを漁ってみて、以下の暫定的な結論にたどり着いた。

大きくわければ、交互作用は２つの意味で使われている。

効果修飾の意味で使っている「交互作用」
２つの要因がともに作用してエンドポイントに効果を及ぼす「交互作用」

しかしながら、この２つがいつでもクリアに分かれているわけではない。

「効果修飾の交互作用」と「ともに作用している交互作用」がくっきりわかれている文脈もあれば、どちらともいえない文脈もある。

また、エンドポイントは、どちらの交互作用の場合も、連続データだったり、割合（リスク）だったり、リスク比、オッズ比、ハザード比などの相対リスクだったり、どちらの場合がどのエンドポイントとも言えない。

解析解析には、統計モデルを使ったり使わなかったりしていて、使う場合がどちらの交互作用で、使わない場合がどちらの交互作用という言い方もできない。

以下に、様々な記述をなるべく有機的なつながりを持って並べてみた。

効果修飾 effect modification の系統

疫学研究の文脈

対象となるメインの曝露要因の因果効果が第２の要因のレベルによって異なるかどうか。→つまり、第２の要因に基づくサブグループ間での、メインの曝露要因の因果効果の変動に焦点を当てている。＋この第２の要因（すなわち、効果修飾要因 effect modifier）自体がアウトカムに影響を与えるかどうかは関係がない。＝目的とする曝露要因の効果が、異なるサブグループ間で異質であるかどうかを評価することが目的である。

http://www.asahikawa-med.ac.jp/dept/mc/healthy/HP2/21_Interaction.pdf

PDF 4枚目

医療統計分野での文脈

医療統計で「交互作用」というと、以下のようなことを指していることがほとんどです。
「アウトカムの群間差（オッズ比やハザード比）がサブグループ間で異なるか、ということ」

交互作用とは？交絡バイアスとの違いやグラフとP値の示し方もわかりやすく解説 | いちばんやさしい、医療統計

生存時間解析の文脈

つまり異質性の検定は2群の累積生存率曲線の非平行性の検定であり、群と生存時間の交互作用の検定に相当します。

http://www.snap-tck.com/room04/c01/stat/stat11/stat1102.html

医薬品の効果の文脈

端的に言えば、”人によって効果が違う”という現象を見る統計学の考え方だと思います。例えば「薬Aが病気Dのリスクを１０パーセント下げる」といったとき、実はその薬は女性では効果がめちゃくちゃあるが男性にはほとんど効かない、なんてことがあるかもしれません。交互作用の考え方を使えば、このように介入の効果が一様でない現象の存在を調べることができます。

「交互作用」とはなにか：介入効果が一様でないときの統計手法～その目的と分類、解釈～ – Unboundedly

層別化後の統合可能性の文脈

xと性の間に交互作用(effect modification)があるといい、男女をプールできない。

http://www.snap-tck.com/room04/c01/stat/stat01/stat0109.html

級内相関係数の文脈

要因Aと要因Bの交互作用がないということは、被検者ごとのb回の測定値の変動パターンが全て同じということです。

http://www.snap-tck.com/room04/c01/stat/stat05/stat0504.html

＞＞もう統計で悩むのは終わりにしませんか？

↑1万人以上の医療従事者が購読中

実験計画法（主に分散分析）の系統

この系統は、「効果修飾」と「ともに作用する」のどちらも含んでいると思うが、「効果修飾」の文脈が多い。

統計モデルを用いた連続データの解析で交互作用を扱うと、「効果修飾」と「ともに作用する」のどちらも含んでいると考えられる。

二元配置分散分析の文脈

通常の二元配置分散分析では一方の要因——この場合は個人差——は効果を分析するのが目的ではなく誤差を減らすのが目的であり、ブロック因子と呼ばれます。では誤差に相当する要因は何でしょうか？それは時期による血圧の変動パターンが被験者によって異なるという要因です。平ったくいえば血圧の下がり具合が個人によって異なっていること、つまり血圧の下がり具合の個人差が誤差になるのです。これを個人(要因A)と時期(要因B)の交互作用(effect modification)といい、要因A×Bと表記します。これが二元配置分散分析における残差になります。この交互作用に対して要因Aと要因Bによる変動のことを主効果といいます。

http://www.snap-tck.com/room04/c01/stat/stat04/stat0401_2.html

このように繰り返しのある二元配置分散分析では要因Aの検定と要因Bの検定、そして要因AとBの交互作用の検定を行うことができます。この場合の交互作用の検定は、効果に関して薬物と食餌の間に相乗効果または相殺効果があるかどうかの検定です。例えば図4.3.2で横軸を食餌の有無とし、縦軸を効果とすると、薬物無−食餌有無のグラフと薬物有−食餌有無のグラフが平行かどうかを検討することによって、効果に関する薬物と食餌の関係が相乗効果(正の交互作用)、相加効果(交互作用無)、相殺効果(負の交互作用)のどれであるかを判定することができます。

http://www.snap-tck.com/room04/c01/stat/stat04/stat0403.html

共分散分析の文脈

ただ、ここで問題になるのは2群の回帰直線の平行性ということです。この例のように2群の回帰直線がほぼ平行の時は良いものの、回帰直線が平行ではなく、クロスしたりするとちょっと面倒なことになります。なぜなら2群の回帰直線が平行ではない時は、投与前値を統一する際、統一する値によって2群の変化量の大小関係が変わってしまい、どちらの群がより低下したか判断できなくなってしまうからです。このように群によって投与前値の影響が異なる時は「投与前値と群の間に交互作用(effect modification)がある」といいます

http://www.snap-tck.com/room04/c01/stat/stat08/stat0801.html

教科書的に言うと、交互作用とは、「ある要因の効果は一定ではなく、他の要因の水準によって異なっている」ような状況を指す。

線形モデルにおける交互作用 – 統計学入門一歩先へ

量的な交互作用と質的な交互作用

量的な交互作用と質的な交互作用も「効果修飾」の範囲と思われる。

以下のリンク先のスライド39枚目、40枚目の図がとても分かりやすい。

http://nfunao.web.fc2.com/files/R-intro/R-stat-intro_09.pdf

Qualitative Interaction（質的な交互作用）もしくは crossover interaction

交互作用による介入・曝露因子の効果の違いは、薬が効きやすい・効きやすくないといった効果の強弱だけに限りません。効果の方向が変わる可能性だってあります。ちなみに疫学では、このように効果の向きを変えてしまう交互作用のことを質的交互作用(Qualitative interaction)と呼びます。

「交互作用」とはなにか：介入効果が一様でないときの統計手法～その目的と分類、解釈～ – Unboundedly

In some cases, we might think that an exposure has a positive effect for one subgroup and a negative effect for a different subgroup. Such instances are sometimes referred as “qualitative interactions” or “crossover interactions”

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 17枚目（p.49)

Quantitative Interaction （量的な交互作用）もしくは non-crossover interaction

The term “quantitative interaction” is sometimes used exclusively for interactions which are not qualitative interactions (Peto,1982). However, others use the term “quantitative interaction” to describe a statistical interaction on any scale, and prefer using “non-crossover interaction” for the presence of interaction which is not a “qualitative interaction” (Gail and Simon, 1985).

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 17枚目（p.49)

分散分析等に対して線形回帰の統計モデルを用いた場合の交互作用は後述する。

ともに作用する交互作用の系統

ともに作用する交互作用の概念

２つのメインの曝露要因がともに作用することで、特定のアウトカムに対する因果効果がどのように変化するのかに注目している。→つまり、メインの曝露要因の因果効果に加えて、第二の曝露要因もアウトカムに対して因果効果を持つ、と仮定している。

http://www.asahikawa-med.ac.jp/dept/mc/healthy/HP2/21_Interaction.pdf

PDF ９枚目

交互作用は2つの因子が組み合わさることで初めて現れる相乗効果のことです。「肥料の量×土の種類」の場合、肥料の量と土の種類が相互に影響を及ぼし合っていることを表します。

30-5. 交互作用とは | 統計学の時間 | 統計WEB

疫学研究の文脈

関連の指標への影響は、加法的な影響（リスク差に対する変化）と乗法的な影響（リスク比やオッズ比に対する変化）の大きく 2 つに分類される。

モデルとして線形モデルを選べば加法的な交互作用の有無を、対数線形モデル、ロジスティックモデルを選べば乗法的な交互作用の有無を検討できる。

https://www.env.go.jp/chemi/ceh/about/advanced/material/guidance20170804.pdf

PDF 8ページ目

加法的交互作用 additive interaction

２つの因子によるそれぞれのリスクを足した値と、２つの因子がともに曝露したときのリスクの値の差が正の時は、加法的交互作用がpositiveもしくはsuper-additive、負の時はnegative もしくは sub-additive、と言う。

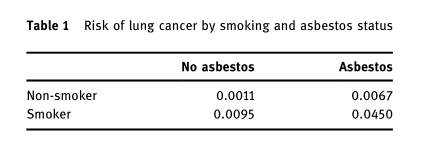
上記の表（Table1）は、喫煙とアスベストの肺がんに対するリスクである。

非喫煙でアスベスト曝露もない人のリスクが0.0011
喫煙だけは0.0095
アスベストだけは0.0067
喫煙とアスベストの両方の場合は0.0450

この時両方の場合のリスクが、それぞれのリスクの和よりも大きければ、super-additiveである。

計算は以下のようにする。

今回の例は、

(0.0450-0.0011) – (0.0095-0.0011) – (0.0067-0.0011) = 0.0299

となって、super-additiveである。

引用・翻訳及び解釈の元は以下のリンク先。

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 3枚目（p.35）

ちなみに、上記の計算結果がゼロのときに、加法的交互作用はない no additive interaction と表現する。

No additive interaction
Positive additive interaction = Super-additive interaction
Negative additive interaction = Sub-additive interaction

こういう対応関係になる。

乗法的交互作用 multiplicative interaction

先ほどのデータ（Table1）で、差ではなく比を使うと、乗法的交互作用のチェックになる。

オッズ比やリスク比を用いることになる。

喫煙とアスベストの両方のリスクと両方なしのリスクの比を、喫煙有り無しのリスク比及びアスベスト有り無しのリスク比の両方で割る。

実際の計算は以下のようにする。

$$ \frac{\frac{0.0450}{0.0011}}{\frac{0.0095}{0.0011}\frac{0.0067}{0.0011}} = 0.7776905 $$

1を超えている場合は、乗法的交互作用がpositive、1未満の場合は、乗法的交互作用がnegativeと判断する。

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 4枚目（p.36）

1のときに、乗法的交互作用がない no multiplicative interaction と表現する。

If the ratio is 1, then the effect of both exposures together is equal to the product
of the effect of the two exposures considered separately, that is, there is no interaction on the multiplicative scale for risk ratios.

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 4枚目（p.36）

No multiplicative interaction
Positive multiplicative interaction = Super-multiplicative interaction
Negative multiplicative interaction = Sub-multiplicative interaction

用語の対応はこのようになる。

オッズ比の加法的・乗法的交互作用

上記Table4について、加法的交互作用は以下のように計算する。

$$ (2.09 – 1) – (1.12 – 1) – (1.21 – 1) = 0.76 > 0 $$

ゼロよりも大きいから加法的交互作用はpositiveである。

乗法的交互作用は以下のように計算する。

$$ \frac{2.09}{1.12 \times 1.21} = 1.54 > 1 $$

1よりも大きいので乗法的交互作用もpositiveである。

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 9枚目（p.41）

Synergism（相乗効果）とAntagonism（拮抗効果）、相加効果

Positive additive interactionは、synergismとも言う。

Negative additive interactionは、antagonismとも言う。

http://www.asahikawa-med.ac.jp/dept/mc/healthy/HP2/21_Interaction.pdf

PDF 10枚目

Positive multiplicative interactionも、synergismと言う。

Negative multiplicative interactionも、antagonismと言う。

http://www.asahikawa-med.ac.jp/dept/mc/healthy/HP2/21_Interaction.pdf

PDF 13枚目

また、相乗効果や拮抗効果を単に交互作用と称することもある。

2つの因子の組み合わせによって生じる相乗効果（拮抗効果）

交互作用とは？交絡バイアスとの違いやグラフとP値の示し方もわかりやすく解説 | いちばんやさしい、医療統計

以下、再掲。

交互作用は2つの因子が組み合わさることで初めて現れる相乗効果のことです。「肥料の量×土の種類」の場合、肥料の量と土の種類が相互に影響を及ぼし合っていることを表します。

30-5. 交互作用とは | 統計学の時間 | 統計WEB

こちらも、再掲。

拮抗効果は、相殺効果とも言う。

交互作用なしの場合は、相加効果と言う。

この文脈は連続データのことであるので、この場合の「交互作用なし」は、「加法的交互作用なし」と思われる。

このように繰り返しのある二元配置分散分析では要因Aの検定と要因Bの検定、そして要因AとBの交互作用の検定を行うことができます。この場合の交互作用の検定は、効果に関して薬物と食餌の間に相乗効果または相殺効果があるかどうかの検定です。例えば図4.3.2で横軸を食餌の有無とし、縦軸を効果とすると、薬物無−食餌有無のグラフと薬物有−食餌有無のグラフが平行かどうかを検討することによって、効果に関する薬物と食餌の関係が相乗効果(正の交互作用)、相加効果(交互作用無)、相殺効果(負の交互作用)のどれであるかを判定することができます。

http://www.snap-tck.com/room04/c01/stat/stat04/stat0403.html

医薬品の効果の文脈で、以下のような記述もある。

単に足しただけでそれ以上の効果がない場合を「相加」と呼んでいるので、やはり加法的交互作用がない場合を「相加効果」と呼ぶと理解できる。

薬物 A（a 用量），薬物 B（b 用量），薬物 A（a 用量）と薬物B（b 用量）との併用での反応値をそれぞれ Ea，Eb，Ea＋b とすると，（中略）Ea＋b ＝ Ea＋Eb＋αとした場合，αが交互作用項である．つまり各薬物の反応値の和以外の成分を交互作用項と設定して，統計的に評価する手法である．交互作用項が検定で有意となる．すなわち，0 でないと判断されれば，相加を超える効果があると考える．αがプラスであれば相乗効果となり，マイナスであれば拮抗効果となる．この解析手法は実験計画法の分野でよく見かける手法であり，一見合理的であるが，薬効を評価する場合には注意する必要がある．

https://www.jstage.jst.go.jp/article/fpj/134/5/134_5_265/_pdf

Sufficient cause interaction

２つの要因それぞれでは生じないが、２つの要因が重なると生じる場合を指す。

Mechanistic interactionでもある。

２つの要因がともに曝露した場合にONになり、一つずつではOFFである。

一つずつの要因では起きなかったことが、２つの要因で生じるという場合、Synergism 相乗効果ともいえる。

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 19枚目（p.51）

統計モデルで検討する交互作用

統計モデルでの検討は、「効果修飾」と「ともに作用」のどちらにも、とらえることができる。

それはサブグループ解析を目的とした「効果修飾」を念頭に置いた分析もできるし、「ともに作用」して効果が変わる交互作用と考えた分析もできるからだ。

2つの要因と統計的交互作用項 statistical interaction term の場合

目的変数がリスク（P）でそのまま無理やり線形モデルを組むとすると以下のようになる。

$$ P = \alpha_0 + \alpha_1 X_1 + \alpha_2 X_2 + \alpha_3 X_1 X_2 $$

この時 $ \alpha_0 $ がどちらも曝露なしのリスク、$ \alpha_1 $ が要因１のリスクと曝露なしのリスク差、 $ \alpha_2 $ が要因２のリスクと曝露なしのリスク差、$ \alpha_3 $ が加法的交互作用である。

この $ \alpha_3 $ を統計的交互作用（statistical interaction）とも言う。

対数線形モデルの場合だと、以下のようになる。

$$ \log{P} = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1 X_2 $$

この時 $ e^{\beta_1} $ が要因１のリスク比、$ e^{\beta_2} $ が要因２のリスク比、$ e^{\beta_3} $ が乗法的交互作用である。

この $ \beta_3 $ が対数線形モデルの統計的交互作用である。

オッズ比のためのロジスティック回帰モデルの場合は、以下のようになる。

$$ \log{\frac{P}{1 – P}} = \gamma_0 + \gamma_1 X_1 + \gamma_2 X_2 + \gamma_3 X_1 X_2 $$

この時 $ e^{\gamma_1} $ が要因のオッズ比、$ e^{\gamma_2} $ が要因２のオッズ比、$ e^{\gamma_3} $ が乗法的交互作用である。

この $ \gamma_3 $ がロジスティック回帰モデルの統計的交互作用である。

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF ９枚目（p.41）

共変量を考慮した場合

Cという記載で一括して共変量を含めたモデル式を以下に掲示する。

共変量が足されても、２つの要因と交互作用項はそのままである。

Often we may want to control for other covariates in models [6][8]. For example, we may want to fit
the following analogous models which include an additional vector of covariates, C:

$$ P = \alpha_0 + \alpha_1 X_1 + \alpha_2 X_2 + \alpha_3 X_1 X_2 + \alpha’_4 C $$

$$ \log{P} = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1 X_2 + \beta’_4 C $$

$$ \log{\frac{P}{1 – P}} = \gamma_0 + \gamma_1 X_1 + \gamma_2 X_2 + \gamma_3 X_1 X_2 + \gamma’_4 C $$

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF 10枚目（p.42）

連続データが目的変数の場合

For additive interaction, a linear regression model for the continuous outcomes could be used

$$ E = \alpha_0 + \alpha_1 X_1 + \alpha_2 X_2 + \alpha_3 X_1 X_2 + \alpha’_4 C $$

and α3 can be taken as a measure of additive interaction. This parameter is equal to the additive interaction
measure:

$$ \alpha_3 = E_{11} – E_{10} – E_{01} + E_{00} $$

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF28枚目（p.60）

X１、X２がともにカテゴリであれば、一般線形モデルによる二元配置分散分析となる。

どちらか一つがカテゴリであれば、交互作用項を投入した共分散分析となる。

両方が連続データであれば、いわゆる重回帰分析で交互作用項あり、ということだ。

For multiplicative interaction, a log-linear regression model for the continuous outcomes could be used

$$ \log{E} = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_1 X_2 + \beta’_4 C $$

and β3 can be taken as a measure of multiplicative interaction. This parameter, when exponentiated, is
equal to the multiplicative interaction measure:

$$ \beta_3 = \frac{E_{11} / E_{10}}{E_{01} / E_{00}} $$

https://cdn1.sph.harvard.edu/wp-content/uploads/sites/603/2018/04/InteractionTutorial_EM.pdf

PDF28枚目（p.60）

ここでEは連続データの期待値という意味で、log(E)は対数変換した連続データの期待値という意味である。

分布形を変更するために対数変換することはあるが、交互作用のために対数変換を考えたことはなく、あまりイメージが沸かない。

ちなみに、添え字の意味は、１１が２つの要因がともにあり、１０は要因１のみあり、０１は要因２のみあり、００は２つの要因ともになしの意味である。