交互作用とは？交絡バイアスとの違いやグラフとP値の示し方もわかりやすく解説

この記事では「交互作用とは？交絡バイアスとの違いやグラフとP値の示し方もわかりやすく解説」ということでお伝えしていきます。

 

• 交互作用とはそもそも何？
• 交互作用と交絡バイアスの違いは？
• 交互作用をグラフ化するには？P値で表すには？

 

といったことを理解できるようになります！

 

交互作用とは？

まずは、交互作用そのものに関して整理しておきましょう。

交互作用は下記のような定義です。

 

 

言葉だけではイメージするのが難しいですが、とにかく「2つの因子の組み合わせ」によって何かしらの効果があるんだな、ということだけはわかりますね。

 

医療統計でいうところの交互作用は？

上記の定義は一般的な交互作用の定義でしたので、医療統計に限定して話をしてみましょう。

医療統計で「交互作用」というと、以下のようなことを指していることがほとんどです。

 

 

図にすると下記の通り。

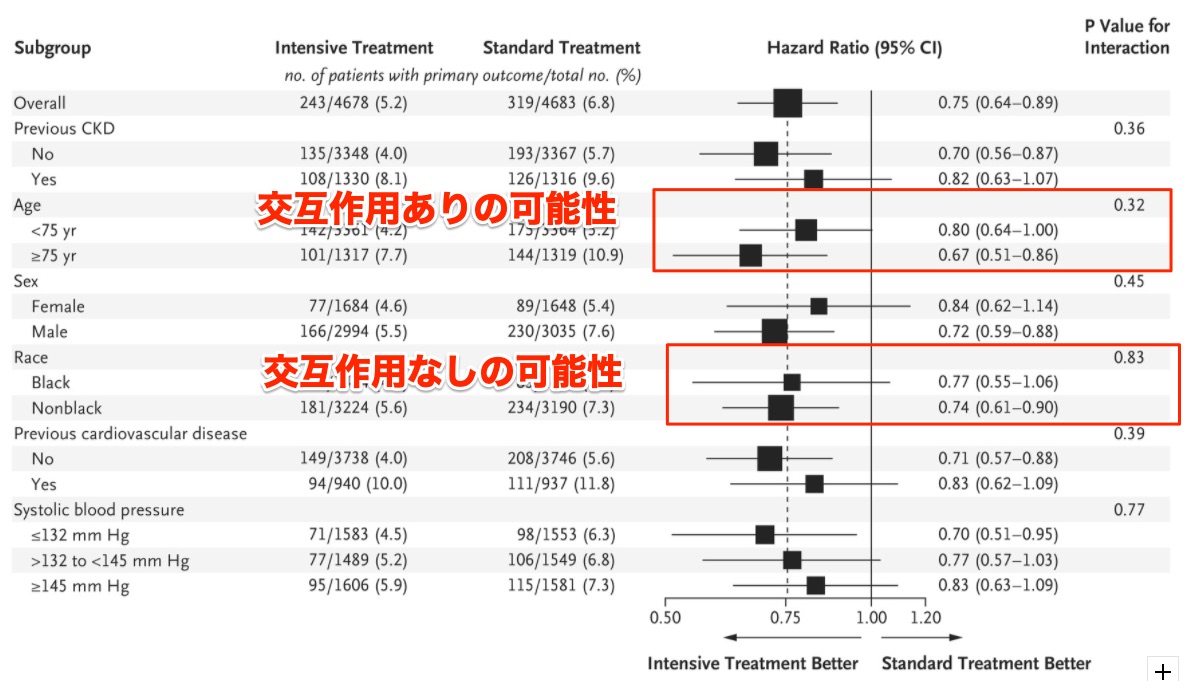
例えばAgeのカテゴリの間「<75yrと>=75yrの間」では、ハザード比が異なっているような図になっています。

一方、Raceのカテゴリの間「BlackとNonblackの間」では、ハザード比は全くといっていいほど異なりません。

上記のうち、「Ageのカテゴリと群に交互作用がある可能性がある」と言えますし、「Raceのカテゴリと群に交互作用がある可能性がない」と言えるのです。

 

交互作用の定義は「2つの因子の組み合わせによって生じる相乗効果（拮抗効果）」でした。

上記のように医療統計では、「あるカテゴリ（AgeやRaceなど）と群との組み合わせで生じるアウトカム（ハザード比など）の違い」ということが言えそうです。

 

交互作用と交絡との違いは？

交互作用が整理できたところで、次は交絡バイアスとの違いを考えてみましょう。

私自身、最初は交互作用と交絡との違いが全くと言っていいほど分からなかったので、あなたにも整理しておいて欲しいなと思います。

 

最初から結論を言っておくと、交互作用と交絡の違いはこの通り。

 

 

これは架空のデータを使って考えていきましょう。

 

架空のデータで交互作用と交絡の違いを考える

用意した架空のデータはこの通り。

• A群20名、B群20名、計40名
• アウトカムはResponse（Yes, No）
• B群のResponseしやすさは男女で同じ
• 男性だとA群でResponseしやすい
• 女性はA群でもB群と同じぐらいのResponseのしやすさ

男性ではA群でResponseしやすい一方で、女性ではA群でもB群と同じぐらいのResponseのしやすさ、という設定。

このとき、性別と群には交互作用がある、と言えますね。

なので、交互作用がある前提で話を進めていきます。

 

そして、2パターンのデータを考えます。

1. A群にもB群にも男女が均等に組み入れられている
2. A群とB群で男女が偏っている

 

1つ目のパターンでは、A群の男性10名、B群の男性10名、A群の女性10名、B群の女性10名、という感じで組み入れられています。

分割表を作成してみると、こんな感じ。

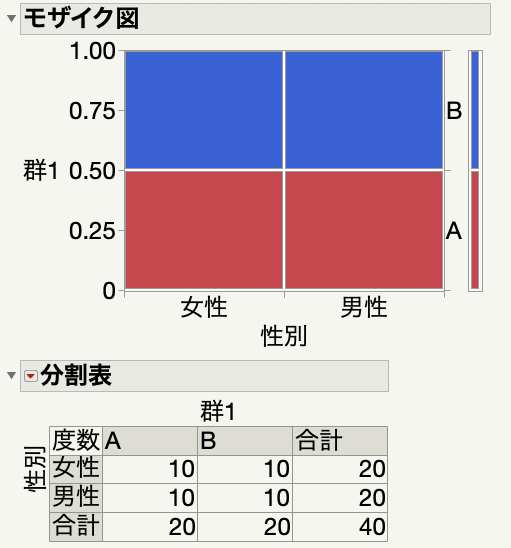
A群にもB群にも男女の偏りはありませんね。

このとき、男性のサブグループでのオッズ比は16であり、男性ではA群のResponseが高い状況です。

女性のサブグループでのオッズ比は1であり、女性では群間でResponseの違いがありません。

つまり、男性女性ごとにオッズ比が違うので交互作用あり、という状況ですね。

 

2つ目のパターンを見てみます。

2つ目のパターンでは、A群の男性15名、B群の男性5名、A群の女性5名、B群の女性15名、という感じで、群ごとに男女の組み入れられ方の偏りがあります。

図にすると下記のとおり。

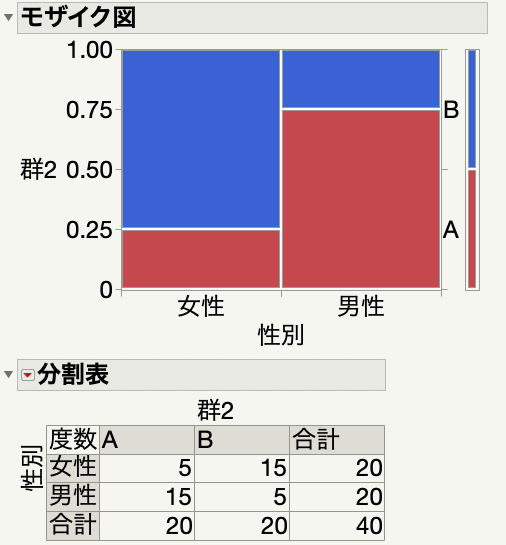
A群とB群とでは、男女の偏りがはっきりとみられます。

このとき、男性のサブグループでのオッズ比は6であり、男性ではA群のResponseが高い状況です。

女性のサブグループでのオッズ比は1であり、女性では群間でResponseの違いがありません。

つまり、男性女性ごとにオッズ比が違うので交互作用あり、という状況ですね。

 

以上をまとめると、「2つのパターンでは男女と群の間で交互作用があることは共通しているが、群に組み入れられている男女比の偏りが違う」ということがわかります。

このときに、どちらに交絡バイアスが入るかを検証したいと思います。

 

交互作用がありそうなものが群間で偏っていると交絡バイアスになる

交絡バイアスが入っているかどうかを確認するには、単変量解析と多変量解析で違いが出るかどうかを確認すればOK。

• 交絡バイアスなし：単変量解析と多変量解析で結果は同じ
• 交絡バイアスあり：単変量解析と多変量解析で結果が異なる

ということで、アウトカムがResponseという2値のカテゴリカルデータですから、ロジスティック回帰分析をやっていきます。

 

パターン1（男女の偏りがない場合）では、単変量解析と多変量解析で以下のような結果になります。

↓単変量解析の結果

↓多変量解析の結果

パターン1だと、単変量解析でも多変量解析でも、それほど群の効果（群に対するP値）が変化していないことがわかります。

 

パターン2（男女の偏りがある場合）では、単変量解析と多変量解析で以下のような結果になります。

↓単変量解析の結果

↓多変量解析の結果

パターン2だと、単変量解析と多変量解析では、群の効果（群に対するP値）が変化していることがわかります。

つまり、交絡バイアスのあるパターン2では、群の効果に明らかに違いが出ている、ということですね。

この場合、性別が交絡因子となって交絡バイアスが引き起こされている、ということです。

 

なので最初に結論をお示しした通り、

 

 

ということが言えます。

 

交互作用と相互作用って違いがある？

交互作用と交絡の違いまでわかったところで、用語の整理です。

交互作用と同じような用語で、相互作用という言葉を聞いたことはないですか？

「交互作用」と「相互作用」はどう違うのでしょうか？

 

これは私のイメージですが、「相互作用」というと、薬に対する交互作用に限定して使われているイメージです。

一方の「交互作用」は、薬に限らず、いろんな研究分野で使われるイメージですね。

 

交互作用に関するグラフとP値は？

では最後に、交互作用に関するグラフ化とP値について整理しておきます。

交互作用を見るためのグラフとしては「フォレストプロット」があります。

フォレストプロットはサブグループ解析を可視化するためのグラフですが、今まで見てきた通り、サブグループ解析をするというのは交互作用を見るということ。

なので、フォレストプロットがそのまま交互作用を見るためのグラフ化になります。

 

そしてP値といえば、P for Interactionが交互作用のP値に該当します。

「Interaction」が「交互作用」の意味ですので、「P for Interaction」がそのまま「交互作用に対するP値」となります。

「交互作用に対するP値」は検出力が低い（有意になりにくい）という性質があるため、一般的に0.2を基準にしてみることが多い印象です。

 

フォレストプロットと交互作用のP値を一つに出力すると、下記の通り。

 

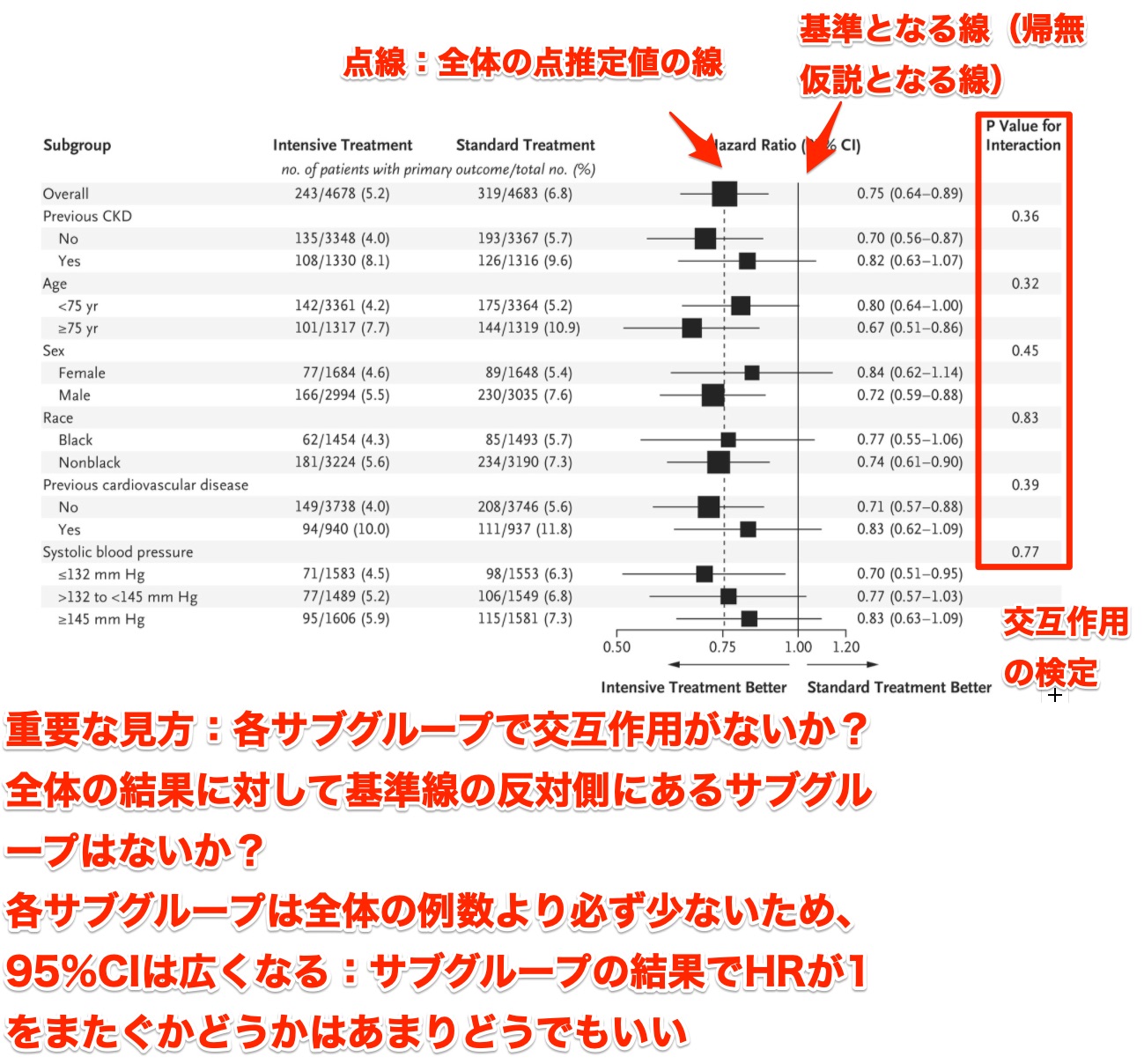
まとめ

いかがでしたか？

この記事では「交互作用とは？交絡バイアスとの違いやグラフとP値の示し方もわかりやすく解説」ということでお伝えしました。

 

• 交互作用とはそもそも何？
• 交互作用と交絡バイアスの違いは？
• 交互作用をグラフ化するには？P値で表すには？

 

といったことを理解できたのなら幸いです！

 

こちらの記事の内容は動画でもお伝えしていますので、あわせてご確認くださいませ。